a mathematical problem solving method that utilizes conversion factors

USING CONVERSION FACTORS TO SOLVE PROBLEMS

We solve many real word problems by converting units within measurement system (metric or customary)  and between measurement systems (customary to metric or metric to customary). 

We use conversion factors to convert units within measurement system and between measurement systems. 

The chart given below can be used to convert units within measurement system. 

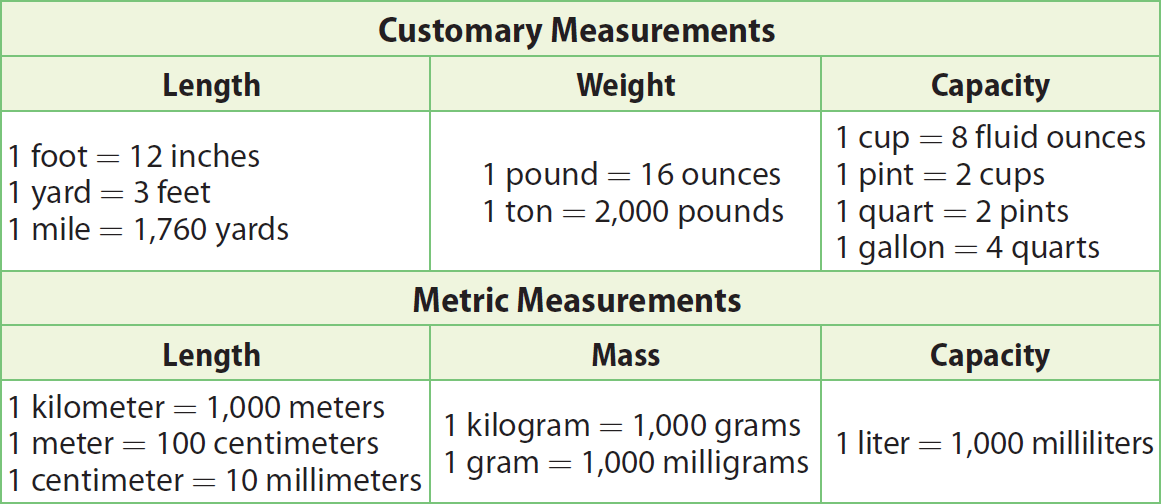
The chart given below can be used to convert units between measurement systems. 

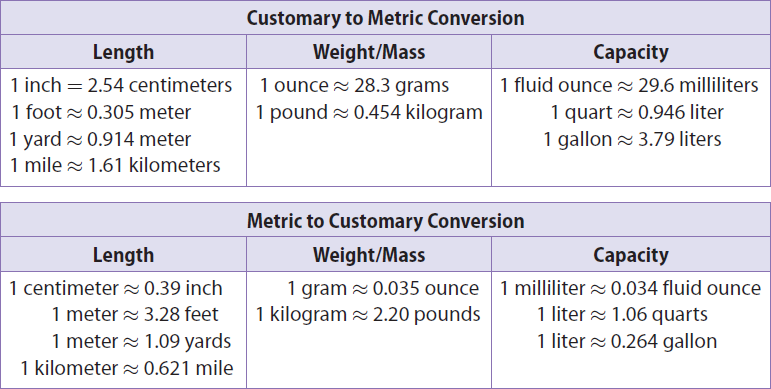
For example, 

From the above chart, in the length section of customary to metric conversion, we have

 1 inch   =  2.54 centimeters

If we convert inches into cm, the conversion factor is 

2.54 cm / 1 inch

If we convert cm into inches, the conversion factor is 

1 inch  / 2.54

Example 1 :

Elena wants to buy 2 gallons of milk but can only find quart containers for sale. How many quarts does she need ?

We want to convert gallons to quarts.

Identify the ratio that compares the units involved.

The units gallons and quarts are customary units of capacity.

Find the relationship of those units in the capacity section of the c ustomary measurements table.

4 quarts  =   1 gallon

The appropriate conversion factor is 4/1.

B ecause when we  multiply 2 gallons by that conversion factor, we can divide out  the common unit gallons. The resulting unit is quarts.

Multiply the given measurement by the conversion factor.

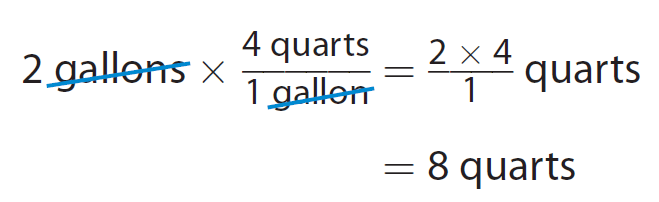
Elena needs 8 quarts of milk.

Example 2 :

A container of a powdered fruit drink mix has a mass of 1.25 kilograms.  What is that mass in milligrams ?

You want to convert kilograms to milligrams.

There is no equation in the table that relates kilograms and  milligrams directly. However, we can convert kilograms to  grams first. Then we can convert grams to milligrams.

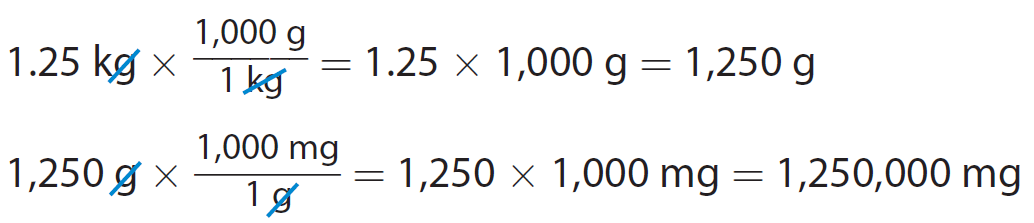
We can also do both conversions at the same time.

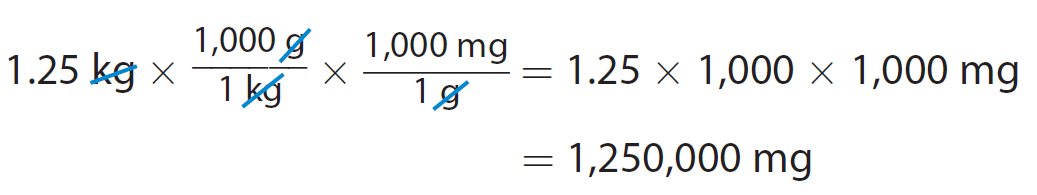
A mass of 1.25 kilograms is equal to 1,250,000 milligrams.

Example 3 :

While working out, Alima adds 11.35 kilograms to the machine.  About how many pounds does she add ?

Find the conversion factor for converting kilograms to pounds

1 kilogram  ≃   2.20 pounds

Write the conversion factor as a ratio

2.20 pounds / 1 kilogram

Convert the given measurement.

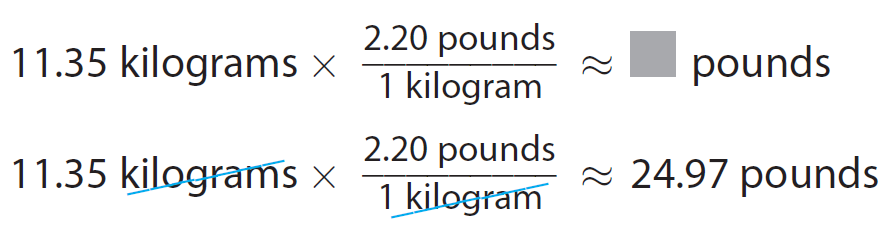
Alima adds about 25 pounds.

Example 4 :

Bob’s driveway is 45 feet long by 18 feet wide. He plans to  pave the entire driveway. The asphalt paving costs $24 per  square meter. What will be the total cost of the paving ?

First find the dimensions of the driveway in meters.

Convert each measurement to meters.

Use 1 foot  ≃  0.305 meter.

Next find the area in square meters.

Area  =  length × width

≃   13.725 × 5.49

≃   75.35025 square meters

Now find the total cost of the paving.

square meters × cost per square meter = total cost

75.35025 × $24   ≃   $1,808.41

Total cost of paving is $1808.41.

Example 5 :

Peter is overweight. He is 105 kg. His aim is to lose 500 g per week. If he manages this, how many weeks will it be until he is 90 kg?

Peter's weight = 105 kg

Each week he is trying to reduce = 500 grams

Number of weeks is taken to have the weight of 90 kg = n

Converting grams to kg

1 kg = 1000 grams

dividing by 2, we get

1/2 kg = 500 grams

0.5 kg = 500 grams

105 - 0.5n = 90

Adding 0.5 n on both sides

105 = 90 + 0.5 n

Subtracting 90 on both sides

105-90 = 0.5n

Dividing by 0.5 on both sides

So, it takes 30 weeks to have the weight of 90 kg.

Example 6 :

30 g serving of a certain breakfast cereal has 0.5 g of salt. How much salt would that be in milligrams

1 gram = 10 milligrams

30 g serving will have 0.5 gram of salt

Converting grams to mg

30 grams = 300 milligrams

From the information,

30 grams of serving = 0.5 grams of salt

300 grams of serving = 10 x 0.5

= 5 grams of salt

Using the conversion above, 

5 grams = 5(10)

= 50 milligrams

Example 7 :

Chase measured a line for his art project. It is 200 millimeters long. How many centimeters is the line?

1 cm = 10 mm ----(1)

200 mm = ? cm

Multiply by 20 on both sides

20 cm = 200 mm

So, the length of the line is 20 cm.

Example 8 :

Cheryl is moving to a new house. Her old house is 3 kilometers from her new house. How many meters is the old house from the new house?

1 km = 1000 meters

3 km = 3(1000)

= 3000 meters

So, the distance between the old house and new house is 3000 meters.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

SAT Math Resources (Videos, Concepts, Worksheets and More)

Dec 23, 24 03:47 AM

Digital SAT Math Problems and Solutions (Part - 91)

Dec 23, 24 03:40 AM

Digital SAT Math Problems and Solutions (Part - 90)

Dec 21, 24 02:19 AM

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

6.2.3: Using Metric Conversions to Solve Problems

• Last updated
• Save as PDF
• Page ID 62187

• The NROC Project

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Solve application problems involving metric units of length, mass, and volume.

Introduction

Learning how to solve real-world problems using metric conversions is as important as learning how to do the conversions themselves. Mathematicians, scientists, nurses, and even athletes are often confronted with situations where they are presented with information using metric measurements, and must then make informed decisions based on that data.

To solve these problems effectively, you need to understand the context of a problem, perform conversions, and then check the reasonableness of your answer. Do all three of these steps and you will succeed in whatever measurement system you find yourself using.

Understanding Context and Performing Conversions

The first step in solving any real-world problem is to understand its context. This will help you figure out what kinds of solutions are reasonable (and the problem itself may give you clues about what types of conversions are necessary). Here is an example.

In the Summer Olympic Games, athletes compete in races of the following lengths: 100 meters, 200 meters, 400 meters, 800 meters, 1500 meters, 5000 meters and 10,000 meters. If a runner were to run in all these races, how many kilometers would he run?

The runner would run 18 kilometers.

This may not be likely to happen (a runner would have to be quite an athlete to compete in all of these races) but it is an interesting question to consider. The problem required you to find the total distance that the runner would run (in kilometers). The example showed how to add the distances, in meters, and then convert that number to kilometers.

An example with a different context, but still requiring conversions, is shown below.

One bottle holds 295 deciliters while another one holds 28,000 milliliters. What is the difference in capacity between the two bottles?

There is a difference in capacity of 1.5 liters between the two bottles.

This problem asked for the difference between two quantities. The easiest way to find this is to convert one quantity so that both quantities are measured in the same unit, and then subtract one from the other.

One boxer weighs in at 85 kilograms. He is 80 dekagrams heavier than his opponent. How much does his opponent weigh?

• \(\ 5 \text { kilograms }\)
• \(\ 84.2 \text { kilograms }\)
• \(\ 84.92 \text { kilograms }\)
• \(\ 85.8 \text { kilograms }\)
• Incorrect. Look at the unit labels. The boxer is 80 dekagrams heavier, not 80 kilograms heavier. The correct answer is 84.2 kilograms.
• Correct. \(\ 80 \text { dekagrams }=0.8 \text { kilograms }\), and \(\ 85-0.8=84.2\).
• Incorrect. This would have been true if the difference in weight was 8 dekagrams, not 80 dekagrams. The correct answer is 84.2 kilograms.
• Incorrect. The first boxer is 80 dekagrams heavier , not lighter than his opponent. This question asks for the opponent’s weight. The correct answer is 84.2 kilograms.

Checking your Conversions

Sometimes it is a good idea to check your conversions using a second method. This usually helps you catch any errors that you may make, such as using the wrong unit fractions or moving the decimal point the wrong way.

A two-liter bottle contains 87 centiliters of oil and 4.1 deciliters of water. How much more liquid is needed to fill the bottle?

The amount of liquid needed to fill the bottle is 0.72 liter.

Having come up with the answer, you could also check your conversions using the quicker “move the decimal” method, shown below.

The amount of liquid needed to fill the bottle is 0.72 liters.

The initial answer checks out. 0.72 liter of liquid is needed to fill the bottle. Checking one conversion with another method is a good practice for catching any errors in scale.

Understanding the context of real-life application problems is important. Look for words within the problem that help you identify what operations are needed, and then apply the correct unit conversions. Checking your final answer by using another conversion method (such as the “move the decimal” method, if you have used the factor label method to solve the problem) can cut down on errors in your calculations.

Unit Conversion: Dimensional analysis

by Donald G Wiggins, M.A./M.S.

Did you know that failure of scientists to use the same unit of measurement resulted in the loss of a $125 million satellite that was supposed to give us weather reports from Mars? This disaster could have been avoided through better communication along with unit conversion by dimensional analysis. “Dimensional analysis” may sound complicated, but this is a method we use in everyday conversions, such as when figuring out how many gallons of gas we can get for $30 or how many donuts are in two dozen.

Most unit conversions can be solved through dimensional analysis, also known as the factor-label method.

Dimensional analysis uses three fundamental facts: (1) A conversion factor is a statement of the equal relationship between two units; (2) Multiplying by a conversion factor in the form of a ratio is multiplying by 1, since the two parts of the ratio equal each other; (3) Units "cancel" when you divide a unit by itself.

The steps in the conversion process are (a) identifying the conversion factor(s) needed, (b) setting up a mathematical problem that uses one or more conversion factors to get to the desired units, and (c) working the math problem, canceling units along the way.

On September 23, 1999, NASA 's $125 million Mars Climate Orbiter approached the red planet under guidance from a team of flight controllers at the Jet Propulsion Laboratory. The probe was one of several planned for Mars exploration, and would stay in orbit around the planet as the first extraterrestrial weather satellite. It had been in flight for over nine months, covering more than 415 million miles of empty space on its way to Mars. As the Orbiter reached its final destination, the flight controllers began to realize that something was wrong. They had planned for the probe to reach an orbit approximately 180 km off the surface of Mars – well beyond the planet's thin atmosphere . But new calculations based on the current flight trajectory showed the Orbiter skimming within 60 km of the Martian surface. Now the probe would actually enter the planet's thin atmosphere, something for which it was never designed. The consequences were catastrophic: when the scientists and engineers commanding the probe lost communication, they could only assume that the spacecraft was incinerated by the friction from an atmospheric entry that it was never supposed to make.

Figure 1: An artists rendition of the Mars Climate Orbiter.

What caused this disaster? The problem arose in part from a simple, seemingly innocent, mistake. Throughout the journey from Earth, solar winds pushed against the solar panels of the probe, throwing the spacecraft off course by a small amount. The designers had planned for this, and jet thrusters were turned on by the flight controllers to apply a force , making numerous small corrections to readjust its course. Unfortunately, the NASA engineers measured this force in pounds (a non-metric unit), while the JPL team worked in Newtons (a metric unit), and the software that calculated how long the thrusters should be fired did not make the proper conversion. Since 1 pound = 4.45 Newtons , 4.45 times too much thrust was applied each time the thrusters were used. While each individual adjustment mistake was very small, this mistake grew larger and larger over multiple adjustments, resulting in the craft's premature demise in the Martian atmosphere .

The Orbiter loss illustrates the need for consistent use of units . Most people, however, are most comfortable working in whatever units they grew up using. As a result, unit consistency may not be possible within or between teams around the world. Ideally, people should be comfortable with a variety of ways of converting units in order to allow for collaboration among individuals from a variety of backgrounds.

While most people are not controlling NASA space probes, unit conversion is something that happens every day, in all walks of life. Even such a simple problem as figuring out that two dozen eggs equals 24 eggs is, at its heart, a unit conversion problem. Whether you realize it or not, when you do this problem in your head, you're figuring it out like this:

Comprehension Checkpoint

• Dimensional Analysis

Generally, unit conversions are most easily solved using a process called dimensional analysis , also known as the factor-label method . A notable exception is the conversions among temperature units (see our Temperature module for details). Dimensional analysis uses three fundamental facts to make these conversions, which lead to the steps in the conversion process:

1. A conversion factor is a statement of the equal relationship between two units . The first step in dimensional analysis is therefore identifying the conversion factor(s) you will need to make your conversion. In the egg problem, the statement that "1 dozen eggs = 12 eggs" is a conversion factor.

2. If you multiply by a conversion factor in the form of a ratio , you are really only multiplying by 1, since the two parts of the ratio equal each other:

The second step in dimensional analysis is therefore to set up a mathematical problem that uses one or more conversion factors to get to the units you are interested in. In the egg problem, if you have 2 dozen eggs and want to know how many individual eggs you have, you would set up the problem like this:

3. Units , just like numbers or variables , "cancel" when you divide a unit by itself. So the final step in dimensional analysis is to work the math problem you've set up, canceling units along the way. In the egg example, the "dozen eggs" in the bottom of the ratio cancels the "dozen eggs" in your original number, leaving "eggs" as the only unit left in the problem, as shown in the final answer, 24 eggs.

Let's apply these steps to a slightly more complex problem than counting eggs? How much money would it cost to fill a truck's 23 gallon gas tank if gas cost $2.87 per gallon?

First, create the conversion factor. Given the price, you can say 1 gallon = $2.87. Then go through and set-up the equations:

Now that you've filled your tank, it's time to head off for your day trip to Mexico. As you cross the border from the US into Mexico, you notice that the speed limit sign reads 100. Wow! Can you step on the gas , or is there something else going on here? There are very few countries other than the United States where you will find speeds in miles per hour – almost everywhere else they would be in kilometers per hour. So, some converting is in order to know what the speed limit would be in a unit you're more familiar with.

First, we need to define what "100 kilometers per hour" means mathematically. The "per" tells you that the number is a ratio: 100 kilometers distance per 1 hour of time. Other than that, you need to know the conversion factor between kilometers and miles, namely 1 mile = 1.61 km. Now the set-up is pretty simple. Give it a try yourself, and then run the animation below (an SWF file, Flash required) or see the equation to reveal the math needed to solve the problem.

• Conversions of multiple units

So far you've seen examples with only one conversion factor, but this method can be used for more complicated situations. When it's time to leave for home from your day trip in Mexico, you realize you have just enough gas to make it back across the border into the US before you have to fill up. You notice that you could buy gas for 6.50 pesos per liter before you head home. At first glance that seems more expensive than the $2.87 per gallon at home, but is it really? You need to convert to be sure. Fortunately you came prepared, and looked up the currency exchange rate (1 peso = 8.95 cents) and volume conversion (1 gallon = 3.79 Liters) the morning before you left.

This conversion is more complicated than the previous examples for two reasons. First, imagine that you do not have a single direct conversion factor for the monetary conversion (pesos to dollars). You know that 1 peso = 8.95 cents, and you also know that 100 cents = 1 dollar. Together, these two facts will let you convert the currency. The second twist is that you are not only changing the money unit – you also need to convert the volume unit as well. These two conversions can be done in a single set-up. The order does not matter, but both must be done. Try to set this one up for yourself first, and then run the animation (an SWF file, Flash required) or see the equation below to reveal the solution:

Notice that when set up properly, the "L" had to be placed above the division bar in the conversion factor in order to cancel out the "L" below the division bar in the original number. Also note that even though the "L" terms are separated by two conversion factors, they still cancel each other out. Now it is easier to decide whether you should fill up before or after you return to the United States.

You can see that you don't have to be an engineer at NASA to need dimensional analysis . You need to convert units in your everyday life (to budget for gas price increases, for example) as well as in scientific applications, like stoichiometry in chemistry and calculating past plate motions in geology. If you know what units you have to work with, and in what units you want your answer to be, you don't need to memorize a formula . If the teams working on the Mars Climate Orbiter had realized that they needed to go through these steps, we would be getting weather forecasts for Mars today.

Table of Contents

Activate glossary term highlighting to easily identify key terms within the module. Once highlighted, you can click on these terms to view their definitions.

Activate NGSS annotations to easily identify NGSS standards within the module. Once highlighted, you can click on them to view these standards.

Chapter 1:Unit 14. Solving Problems with single or multi-step Conversion Factors

Problem solving with conversion factors.

This process is called dimensional analysis. A general problem solving method in which the different units are associated with numbers and final result is calculate by converting one unit to another unit. calc. is set up from unit cancellation to target unit.

Step#1: Identify the units of known or given quantity and the units of target quantity Step#2: Figure out the conversion factors required from given unit to target unit. Step#3: Multiply the given quantity by one or more conversion factors in such a manner that the original units are canceled leaving only the desired unit.

Watch this out to solve drug dosage related problems that require conversion factors.

Example Problem: (A)      A dose of 250 mg of acetaminophen is prescribed for a 20-kg child. How many ml of Children’s Tynenol (100. mg of acetaminophen per 2.5 ml) are needed?

Step#1: Identify given and target quantity and numbers:

Given: 250mg             target: ml Step#2: Write the conversion factors:

Provided in the problem:                    2.5 ml                                                                 100 mg

Step#3. Multiply the given quantity by the conversion factor.

250 mg ×  2.5 ml      =  6.3ml (lowest 2 sig fig) 100 mg

Check: the answer is reasonable. Since the required dose is larger than standard dose, volume would be larger than standard.

Nurses Conversion units for drugs Drug   Calculations  

Drug calculations vary depending on whether you are dealing with liquid or solid medications, or if the dose is to be given over a period of time. In this section I will go over each of these situations in turn.

It is very important that you know how drug dosages are worked out, because it is good practice to always check calculations before giving medication, no matter who worked out the original amount. It is far better to point out a mistake on paper than overdose a patient.

a)   Tablets

Working out dosage from tablets is simple.

Formula for dosage:

Total dosage required  = Number of tablets required Dosage per tablet

Note-If your answer involves small fractions of tablets, it would be more sensible to try to find tablets of a different strength rather than try to make 1/3  of a tablet for example. Examples

• A patient needs 500mg of X.  X comes in 125mg tablets. How many tablets per day does he need to take?

Total dosage required is 500mg, Dosage per tablet is 125mg So our calculation is 5 0 0 = 4 He needs 4 tablets a day

b)  Liquid Medicines Liquid medicines are a little trickier to deal with as they will contain a certain dose within a certain amount of liquid, such as 250mg in 50ml, for example. To work out the dosage, we use the formula: What you want   × What it’s in What you’ve got

Examples 2)We need a dose of 500mg of Y. Y is available in a solution of 250mg per 50ml.

In this case,

What we want = 500 What we’ve got = 250 What it’s in = 50

So our calculation is 5 0 0 × 50 =100 250

We need 100ml of solution. 3) We need a dose of 250mg of Z is available in a solution of 400mg per 200ml. In this case,

What we want = 250 What we’ve got = 400 What it’s in = 200

So our calculation is 2 5 0 × 200 = 125 400

We need 125ml of solution. Medicine over Time 1) Tablets/liquids This differs from the normal calculations in that we have to split our answer for the total dosage into 2 or more smaller doses.

Look at Example 1 again. If the patient needed the 500mg dose to last the day, and tablets were taken four times a day, then our total of 4 tablets would have to be split over 4 doses.

Total amount of liquid/tablets for day = Amount to be given per dose Number of doses per day

We would perform the calculation: 4÷4=1 So he would need 1 tablet 4 times a day. 2)   Drugs delivered via infusion For calculations involving infusion, we need the following information:

• The total dosage required
• The period of time over which medication is to be given
• How much medication there is in the solution

Example 4)A patient is receiving 500mg of medicine X over a 20 hour X is delivered in a solution of 10mg per 50ml. What rate should the infusion be set to? Here our total dosage required is 500mg Period of time is 20 hours

There are 10mg of X per 50ml of solution

Firstly we need to know the total volume of solution that the patient is to receive. Using the formula for liquid dosage we have:

500 ×50=2500 So the patient needs to receive 2500mls. 10 We now divide the amount to be given by the time to be taken:              2 5 0 0

The patient needs 2500mls to be given at a rate of 125mls per hour

d)  Drugs labelled as a percentage Some drugs may be labelled in different ways to those used earlier. V/V and W/V Some drugs may have V/V or W/V on the label. V/V means that the percentage on the bottle corresponds to volume of drug per volume of solution i.e 15% V/V means for every 100ml of solution, 15ml is the drug. W/V means that the percentage on the bottle corresponds to the weight of drug  per volume  of solution.  Normally this is of the form ‘number of grams per number of millilitres’. So in this case 15% W/V means that for every 100ml of solution there are 15 grams of the drug.

If we are converting between solution strengths, such as diluting a 20% solution to make it a 10% solution, we do not need to know whether the solution is V/V or W/V. Examples 5. We need to make up 1 litre of a 5% solution of We have stock solution of 10%. How much of the stock solution do we need? How much water do we need?

We can adapt the formula for liquid medicines here:

What we want           ×  What we want it to be in What we’ve got

We want a 5% solution. This is same as 5/100 or 1/20. We’ve got a 10% solution. This is the same as 10/100 or 10 . We want our finished solution to have a volume of 1000ml. Our formula becomes: ( 1/20)   * 1000                                   (1/10)

(using the rule for dividing fractions)

= 1/2×1000 = 500 .

We need 500mls of the A solution.

Which means we need 1000 – 500 = 500mls of water.

(Alternatively you can use the fact that a 5% solution is half the strength of a 10% solution to see that you need 500ml of solution and 500ml of water) 6.)You have a 20% V/V solution of drug The patient requires 30ml of the drug. How much of the solution is required?

20% V/V means that for every 100ml of solution we have 20ml of drug F. Using our formula:

What you want   × What it’s in What you’ve got

This becomes 30 ×100 = 150 We need 150mls of solution. 7)Drug G comes in a W/V solution of 5%. The patient requires 15 grams of How many mls of solution are needed?

5% W/V means that for every 100mls of solution, there are 5 grams of G. Using the formula gives us 15 ×100 = 300

300mls of solution are required.

Other Dimensional analysis problem example: B) A person is driving a car with a speed of 229.8 km/h. What is the speed in 1) Miles per hour 2) Feet per second

Given 1 km= 0.6214 mile 1000m= 1km,  1 m= 3.28 ft, 60 sec=1min and 60 min= 1 hr 1)Step#1: Identify given and target quantity and numbers: Given: 229.8km/hr                  target: mi/hr Step#2: Write the conversion factors:

Provided in the problem:                    0.6214 mi                                                             1 km Step#3. Multiply the given quantity by the conversion factor.

229.8 km ×  0.6214 mi      =  143.4mi/hr (lowest 4 sig fig used in problem) 1 km Step#1: Identify given and target quantity and numbers:

Given: 229.8km/hr                  target: ft/s

Step#2: Write the conversion factors:

Provided in the problem:                    3.28 ft & 0.6214 mi                                                                    1 m          1 km

1 hr,              1 min

60 min           60 sec

229.8 km ×  1000m  × 3.28 ft   × 1 hr       × 1 min      1hr                       1 km         1 m        60 min      60 sec

=  209 ft/s ( lowest 3 sig fig used in calc).

For more information watch this out:

For more practice visit:

1.  If one teaspoon contains 5.0 ml, how many teaspoons of Children Tylenol (100. mg of acetaminophen per 2.5 ml) are needed for a child with a dose of 240 mg?

2. A patient is prescribed 0.150mg of a drug that is available in 25 μg tablets.How many tablets are needed?

3. how many milliliters of Children’s Mortin (100 mg of ibuprofen per 5 ml) are needed to give a child a dose of 180 mg?

4. A chemist synthesized 0.510 kg of aspirin in the lab. If the normal doses of aspirin is two 325 mg tablets, how many doses did she prepare?

5.  A patient requires 3.0 pt of blood during surgery. How many liters does this correspond to?

given  1qt= 2 pt, 1 L=1.06 qt

6. A patient is prescribed 2.0 g of medication to be taken four times a day. If the medicine is available in 500 mg tablets, how many tablets are needed in a 24. hr period?

Ans: 1. 9 ml

2.6 tablets

3. 1.2 teaspoon

4. 785 doses

6. 16 tablets

• For more practice: Go to the following website for online tutorial on Unit conversion: http://joneslhs.weebly.com/ Unit Conversion Tutorial                
• Go to the following website:  http://joneslhs.weebly.com
• Click on the  Learn  button on the left. Read the tutorial first.  When you think that you understand the idea, go back to the Main Menu and click on  One Step Conversions .
• For problems 1, 2, and 3 write down what the completed problem looks like. Cancel the units that cancel.  Circle the unit that doesn’t cancel.  Write down the answer to the problem.

For problems 4-9, you can just write down the answer once you have solved it.

• Calculated Answer:

For problem 10, solve it on paper here.  Then type in the calculated answer to see if you are correct.

• Solved problem and answer:

WHEN YOU ARE DONE, SHOW YOUR WORK TO YOUR INSTRUCTOR BEFORE MOVING ON TO A MORE CHALLENGING LEVEL.

Multi-Step Conversions                       Name: ___________________________________

• For problems 1, 2, and 3 write down what the completed problem looks like. Cancel the units that cancel.  Circle the unit that is the one left at the end.  Write down the answer to the problem.

For problems 4-10, you can just write down the answer once you have solved it.

Name: ___________________________________

Double Unit Conversions

• Read the directions on the first problem to see how to get started. Work through the challenging problems recording your answer for each one.   Don’t forget units!
• For problem 6, solve it on paper here. Then type in the calculated answer to see if you are correct.

Cubed and Squared Conversions

• Read the directions on the first problem to see how to get started. Work through the challenging problems recording your answer for each one. Don’t forget units!
• For problem 4, solve it on paper here. Then type in the calculated answer to see if you are correct.

The following classroom resources has been taken from AACT.

Cupcake Conversions, from Bench to Bakery

All consumer products start as a small batch to formulate ideal qualities but are scaled up to mass production for consumer purchase. In this process troubleshooting is essential to maintain quality and consistency of product.

You will take on the role of a successful baker who has an award winning recipe for cupcakes which is going to be scaled up to commercial baking. To achieve this end goal you will look at conversions from English units to Metric units and then standardize all units to grams regardless of ingredients. Finally you will look at issues on a microscale of production and see how they would affect macroscale baking of the product.

• Convert measurements from English to the International Units of Measurement (Metric).
• Scale up measurements for a standard recipe to a larger quantity.
• Trouble shoot problems encountered with scaling up a product from bench to bakery (small to larger quantities).
• Read the recipe for a vanilla cupcake below:
• You live in a global society and you realize that this recipe should be out there for the rest of the world. Unfortunately, the rest of the world (except for the United States, Liberia and Myanmar) doesn’t use the English Standard of measurement. They all use the International System of Measurement, or the Metric scale. Please convert each of the measurements below from English Standard to Metric.a)How many grams are in 2 cups of wheat flour if 1 cup is 120.00 grams? Remember to use dimensional analysis to solve this problem.

Starting unit x Conversion = Answer

2.00  Cups of Flour                   x           120.00 grams  =         240. g

1.00  Cup of Flour

Note that the units are cancelled because anything divided by itself is the value of 1.00.

b) How many grams are in ½ teaspoon of salt if 5.00 grams of salt are in 1.00 teaspoon?

c) How many grams are in 2 teaspoons of baking powder if 4.60 grams of baking powder are in 1.00 teaspoon?d)

d) How many grams are in ½ cup of unsalted butter if there are 227.00 grams of butter in 1.00 cup?

e) How many grams of sugar are in ¾ cup of sugar if there are 200.00 grams of sugar in 1.00 cup?

f) What is the mass of 2 eggs if the mass of an average egg is 2.00 ounces? There are 28.50 grams per ounce.  You must first convert from the number of eggs to ounces and then the number of ounces to grams.

g) How many grams of milk are in 1 cup of milk if there are 473.176 mL of milk in 2.00 cups and the density of milk is 1.027 grams/mL? You must first convert the cups of milk to milliliters and then convert milliliters to grams using the density.  Remember use dimensional analysis.

h) How many grams of vanilla extract are in 1 teaspoon vanilla extract if 1.00 teaspoon is 0.15 fluid ounces and 1.00 fluid ounce is 28.35 grams? You must first convert the teaspoon to fluid ounces and then the fluid ounces to grams.  Remember to use dimensional analysis.

• Convert the baking temperature of 375  o F to Celsius. a) Why Celsius? Watch the video to understand the difference between the two scales. b) Use the following formula for the conversion: T (°C)  = (T (F)  – 32) x 5/9j) Successful bakeries don’t just make one batch of anything. In order to be competitive this recipe must be scaled up. How much of each ingredient would be required to make 200 cupcakes? Fill in the table below with your scale up information.

Scaling up is not as simple as taking the basic ingredients and then multiplying by a factor to get the total quantity. So many variables can affect the outcome.

• Using the graphic organizer below, brainstorm at least three issues that could arise when baking cupcakes (i.e. what could go wrong) at the micro-level (home/test kitchen).
• Using the graphic organizer below, brainstorm at least three issues that could arise when baking cupcakes (i.e. what could go wrong) at the macro-level (commercial bakery).
• Share your thoughts with at least one other person in class. Fill in ideas that you didn’t have in your graphic organizer.
• Be prepared to share your ideas during the teacher lead discussion.
• Ensure that the final product (the 200 cupcakes) maintains its quality and consistency.
• Provide the final recipe, in grams, to the bakery manager.b) Putting yourself in the role of the bakery manager explain why you will still need to do testing to ensure quality control.

Answer Key:  Cupcake Conversions, from Bench to Bakery

*Note that not all answers are calculated using significant digits.

• You live in a global society and you realize that this recipe should be out there for the rest of the world. Unfortunately, the rest of the world (except for the United States, Liberia and Myanmar) doesn’t use the English Standard of measurement. They all use the International System of Measurement, or the Metric scale. Please convert each of the measurements below from English Standard to Metric.k) How many grams are in 2 cups of wheat flour if 1 cup is 120.00 grams? Remember to use dimensional analysis to solve this problem.

2.00  Cups of Flour                x       120.00 grams      =      240. g

Note that the units are cancelled because anything divided by itself is the value of 1.00. l) How many grams are in ½ teaspoon of salt if 5.00 grams of salt are in 1.00 teaspoon?

0.5  teaspoons of salt     x       5.00 grams          =                      2.50 g

1.00  teaspoons of salt

 m)  How many grams are in 2 teaspoons of baking powder if 4.60 grams of baking powder are in 1.00 teaspoon?

2.00  teaspoons of baking powder      x       4.60 grams          =      9.20 g

1.00  teaspoons of baking powder

n) How many grams are in ½ cup of unsalted butter if there are 227.00 grams of butter in 1.00 cup?

0.50  Cups of butter       x       227.00 grams      =      113.5 g

1.00  Cup of butter

o) How many grams of sugar are in ¾ cup of sugar if there are 200.00 grams of sugar in 1.00 cup?

.75  Cups of sugar         x       200.00 grams      =      150.00 g

1.00  Cup of sugar

p)  What is the mass of 2 eggs if the mass of an average egg is 2.00 ounces? There are 28.50 grams per ounce. You must first convert from the number of eggs to ounces and then the number of ounces to grams.

2  eggs        x       2.00  ounce  x        28.50 grams        =      114 g

1  egg                 1  ounce

q) How many grams of milk are in 1 cup of milk if there are 473.176 mL of milk in 2.00 cups and the density of milk is 1.027 grams/mL? You must first convert the cups of milk to milliliters and then convert milliliters to grams using the density.  Remember use dimensional analysis.

1  cup of milk                x       473.176  mL         x        1.027 grams        =        242.98 g

2  cups of milk      1  mL

r) How many grams of vanilla extract are in 1 teaspoon vanilla extract if 1.00 teaspoon is 0.15 fluid ounces and 1.00 fluid ounce is 28.35 grams? You must first convert the teaspoon to fluid ounces and then the fluid ounces to grams.  Remember to use dimensional analysis.

1  tsp vanilla         x       0.15  fl. ounce       x        28.35 grams        =        4.25 g

1  tsp                          1  fl. ounce

s)  Convert the baking temperature of 375  o F to Celsius. a)Why Celsius? Watch the  Temperature Guys video  to understand the difference between the two scales. b) Use the following formula for the conversion: T (°C)  = (T (F)  – 32) x 5/9

190.5 °C t)  Successful bakeries don’t just make one batch of anything. In order to be competitive this recipe must be scaled up. How much of each ingredient would be required to make 200 cupcakes? Fill in the table below with your scale up information.

• Using the graphic organizer below, brainstorm at least three issues that could arise when baking cupcakes (i.e. what could go wrong) at the micro-level (home/test kitchen). Answers will vary, refer to PPT.
• Using the graphic organizer below, brainstorm at least three issues that could arise when baking cupcakes (i.e. what could go wrong) at the macro-level (commercial bakery). Answers will vary, refer to PPT.
• Provide the final recipe, in grams, to the bakery manager.

Answers will vary, some possibilities include:

• Production baker needs to calibrate ovens.
• Production baker might have different equipment so it will be different at larger scales so he/she will still need to trouble shoot batches of cupcakes.
• He/she should change variables, collect data, and send the results back to the original baker so that trouble shooting can occur back at the micro level. This is what happens in industry with product development.d) Putting yourself in the role of the bakery manager explain why you will still need to do testing to ensure quality control.

Username or Email Address

Remember Me

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

3.1: Problem Solving and Unit Conversions

• Last updated
• Save as PDF
• Page ID 365755

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

Learning Objectives

• Given a quantity, convert from one set of units to another using dimensional analysis showing canceling on units. This includes one factor conversions.

During your studies of chemistry (and physics also), you will note that mathematical equations are used in many different applications. Many of these equations have a number of different variables with which you will need to work. You should also note that these equations will often require you to use measurements with their units. Using the correct units is critical!

Converting Between Units with Conversion Factors

A conversion factor is a ratio used to convert one unit of measurement into another. A simple conversion factor can convert meters into centimeters, for example. Since most calculations require measurements to be in certain units, you will find many uses for conversion factors. Always remember that a conversion factor has to represent a fact; this fact can either be simple or more complex. For instance, you already know that 12 eggs equal 1 dozen. A more complex fact is that the speed of light is \(1.86 \times 10^5\) miles/\(\text{sec}\). Either one of these can be used as a conversion factor depending on what type of calculation you are working with.

*Pounds and ounces are technically units of force, not mass, but this fact is often ignored by the non-scientific community.

Of course, there are other ratios which are not listed in Table \(\PageIndex{1}\). They may include:

• Ratios embedded in the text of the problem (using words such as per or in each , or using symbols such as / or %).
• Conversions in the SI system, as covered in the last chapter.
• Conversions in the English system (such as 12 inches \(=\) 1 foot or 4 quarts \(=\) 1 gallon).
• Time conversions (such as 60 seconds \(=\) 1 minute or 60 minutes \(=\) 1 hour).

If you learned the SI units and prefixes described, then you know that 1 cm is 1/100th of a meter.

\[ 1\; \rm{cm} = \dfrac{1}{100} \; \rm{m} = 10^{-2}\rm{m}\]

\[100\; \rm{cm} = 1\; \rm{m}\]

Suppose we divide both sides of the equation by \(1 \text{m}\) (both the number and the unit):

\[\mathrm{\dfrac{100\:cm}{1\:m}=\dfrac{1\:m}{1\:m}}\]

As long as we perform the same operation on both sides of the equals sign, the expression remains an equality. Look at the right side of the equation; it now has the same quantity in the numerator (the top) as it has in the denominator (the bottom). Any fraction that has the same quantity in the numerator and the denominator has a value of 1:

\[ \dfrac{ \text{100 cm}}{\text{1 m}} = \dfrac{ \text{1000 mm}}{\text{1 m}}= \dfrac{ 1\times 10^6 \mu \text{m}}{\text{1 m}}= 1\]

We know that 100 cm is 1 m, so we have the same quantity on the top and the bottom of our fraction, although it is expressed in different units.

Performing Dimensional Analysis

Dimensional analysis is amongst the most valuable tools that physical scientists use. Simply put, it is the conversion between an amount in one unit to the corresponding amount in a desired unit using various conversion factors.

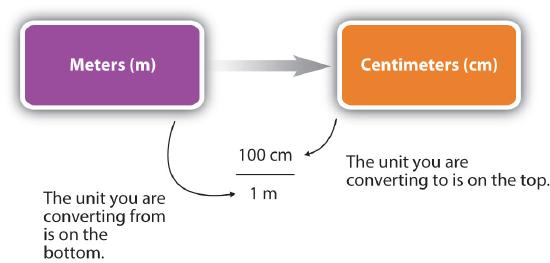
Here is a simple example. How many centimeters are there in 3.55 m? Perhaps you can determine the answer in your head. If there are 100 cm in every meter, then 3.55 m equals 355 cm. To solve the problem more formally with a conversion factor, we first write the quantity we are given, 3.55 m. Then we multiply this quantity by a conversion factor, which is the same as multiplying it by 1. We can write 1 as \(\mathrm{\frac{100\:cm}{1\:m}}\) and multiply:

\[ 3.55 \; \rm{m} \times \dfrac{100 \; \rm{cm}}{1\; \rm{m}}\]

The 3.55 m can be thought of as a fraction with a 1 in the denominator. Because m, the abbreviation for meters, occurs in both the numerator and the denominator of our expression, they cancel out:

\[\dfrac{3.55 \; \cancel{\rm{m}}}{ 1} \times \dfrac{100 \; \rm{cm}}{1 \; \cancel{\rm{m}}}\]

The final step is to perform the calculation that remains once the units have been canceled:

\[ \dfrac{3.55}{1} \times \dfrac{100 \; \rm{cm}}{1} = 355 \; \rm{cm}\]

In the final answer, we omit the 1 in the denominator. Thus, by a more formal procedure, we find that 3.55 m equals 355 cm. A generalized description of this process is as follows:

quantity (in old units) × conversion factor = quantity (in new units)

You may be wondering why we use a seemingly complicated procedure for a straightforward conversion. The conversion problems you encounter will not always be so simple . If you master the technique of applying conversion factors, you will be able to solve a large variety of problems.

In the previous example, we used the fraction \(\frac{100 \; \rm{cm}}{1 \; \rm{m}}\) as a conversion factor. Does the conversion factor \(\frac{1 \; \rm m}{100 \; \rm{cm}}\) also equal 1? Yes, it does; it has the same quantity in the numerator as in the denominator (except that they are expressed in different units). Why did we not use that conversion factor? If we had used the second conversion factor, the original unit would not have canceled, and the result would have been meaningless. Here is what we would have gotten:

\[ 3.55 \; \rm{m} \times \dfrac{1\; \rm{m}}{100 \; \rm{cm}} = 0.0355 \dfrac{\rm{m}^2}{\rm{cm}}\]

For the answer to be meaningful, we have to construct the conversion factor in a form that causes the original unit to cancel out . Figure \(\PageIndex{1}\) shows a concept map for constructing a proper conversion.

General Steps in Performing Dimensional Analysis

• Identify the " given " information in the problem. Look for a number with units to start this problem with.
• What is the problem asking you to " find "? In other words, what unit will your answer have?
• Use ratios and conversion factors to cancel out the units that aren't part of your answer, and leave you with units that are part of your answer.
• When your units cancel out correctly, you are ready to do the math . You are multiplying fractions, so you multiply the top numbers and divide by the bottom numbers in the fractions.

Significant Figures in Conversions

How do conversion factors affect the determination of significant figures?

• Numbers in conversion factors based on SI definitions, such as kilograms to grams, are not considered in the determination of significant figures in a calculation because the numbers in such conversion factors are exact.
• Conversions within the English system are also exact. The numbers in conversion factors from one English unit to another English unit do not effect the significant figures in the answer.
• Counted numbers are also exact. If there are 16 students in a classroom, the number 16 is exact.
• In contrast, conversion factors that come from measurements (such as density, as we will see shortly) have a limited number of significant figures and should be considered in determining the significant figures of the final answer.
• Conversions between the SI and English systems are not exact. The significant figures in the conversion must be considered when determining the significant figures in the answer. The one exception is the conversion between inches and centimeters (1 in = 2.54 cm) which is exact.

Example \(\PageIndex{1}\)

Exercise \(\pageindex{1}\).

Perform each conversion.

• 101,000 ns to seconds
• 32.08 kg to grams
• 1.53 grams to cg

Contributions & Attributions

This page was constructed from content via the following contributor(s) and edited (topically or extensively) by the LibreTexts development team to meet platform style, presentation, and quality:

Marisa Alviar-Agnew  ( Sacramento City College )

Henry Agnew (UC Davis)