matrix representation of graph in data structure

DSA Tutorial

Linked lists, stacks & queues, hash tables, shortest path, minimum spanning tree, maximum flow, time complexity, dsa reference, dsa examples.

A Graph is a non-linear data structure that consists of vertices (nodes) and edges.

A vertex, also called a node, is a point or an object in the Graph, and an edge is used to connect two vertices with each other.

Graphs are non-linear because the data structure allows us to have different paths to get from one vertex to another, unlike with linear data structures like Arrays or Linked Lists.

Graphs are used to represent and solve problems where the data consists of objects and relationships between them, such as:

• Social Networks: Each person is a vertex, and relationships (like friendships) are the edges. Algorithms can suggest potential friends.
• Maps and Navigation: Locations, like a town or bus stops, are stored as vertices, and roads are stored as edges. Algorithms can find the shortest route between two locations when stored as a Graph.
• Internet: Can be represented as a Graph, with web pages as vertices and hyperlinks as edges.
• Biology: Graphs can model systems like neural networks or the spread of diseases.

Graph Properties

Use the animation below to get an understanding of the different Graph properties, and how these properties can be combined.

A weighted Graph is a Graph where the edges have values. The weight value of an edge can represent things like distance, capacity, time, or probability.

A connected Graph is when all the vertices are connected through edges somehow. A Graph that is not connected, is a Graph with isolated (disjoint) subgraphs, or single isolated vertices.

A connected Graph depending on if it is directed or not:

• We have an undirected connected Graph is if you can go along the edges in the Graph from one node, to every other node in the Graph.
• A strongly connected directed Graph is if you can start at any node and reach every other node in the Graph along the directed edges.
• A weakly connected directed Graph is if you can reach all nodes from any node, when disregarding the direction of the edges.

A directed Graph, also known as a digraph, is when the edges between the vertex pairs have a direction. The direction of an edge can represent things like hierarchy or flow.

A cyclic Graph is defined differently depending on whether it is directed or not:

• A directed cyclic Graph is when you can follow a path along the directed edges that goes in circles. Removing the directed edge from F to G in the animation above makes the directed Graph not cyclic anymore.
• An undirected cyclic Graph is when you can come back to the same vertex you started at without using the same edge more than once. The undirected Graph above is cyclic because we can start and end up in vertes C without using the same edge twice.

A loop , also called a self-loop, is an edge that begins and ends on the same vertex. A loop is a cycle that only consists of one edge. By adding the loop on vertex A in the animation above, the Graph becomes cyclic.

Graph Representations

A Graph representation tells us how a Graph is stored in memory.

Different Graph representations can:

• take up more or less space.
• be faster or slower to search or manipulate.
• be better suited depending on what type of Graph we have (weighted, directed, etc.), and what we want to do with the Graph.
• be easier to understand and implement than others.

Below are short introductions of the different Graph representations, but Adjacency Matrix is the representation we will use for Graphs moving forward in this tutorial, as it is easy to understand and implement, and works in all cases relevant for this tutorial.

Graph representations store information about which vertices are adjacent, and how the edges between the vertices are. Graph representations are slightly different if the edges are directed or weighted.

Two vertices are adjacent, or neighbors, if there is an edge between them.

Adjacency Matrix Graph Representation

Adjacency Matrix is the Graph representation (structure) we will use for this tutorial.

How to implement an Adjacency Matrix is shown on the next page.

The Adjacency Matrix is a 2D array (matrix) where each cell on index (i,j) stores information about the edge from vertex i to vertex j .

Below is a Graph with the Adjacency Matrix representation next to it.

The adjacency matrix above represents an undirected Graph, so the values '1' only tells us where the edges are. Also, the values in the adjacency matrix is symmetrical because the edges go both ways (undirected Graph).

To create a directed Graph with an adjacency matrix, we must decide which vertices the edges go from and to, by inserting the value at the correct indexes (i,j) . To represent a weighted Graph we can put other values than '1' inside the adjacency matrix.

Below is a directed and weighted Graph with the Adjacency Matrix representation next to it.

In the adjacency matrix above, the value 3 on index (0,1) tells us there is an edge from vertex A to vertex B, and the weight for that edge is 3 .

As you can see, the weights are placed directly into the adjacency matrix for the correct edge, and for a directed Graph, the adjacency matrix does not have to be symmetric.

Adjacency List Graph Representation

In case we have a 'sparse' Graph with many vertices, we can save space by using an Adjacency List compared to using an Adjacency Matrix, because an Adjacency Matrix would reserve a lot of memory on empty Array elements for edges that don't exist.

A 'sparse' Graph is a Graph where each vertex only has edges to a small portion of the other vertices in the Graph.

An Adjacency List has an array that contains all the vertices in the Graph, and each vertex has a Linked List (or Array) with the vertex's edges.

In the adjacency list above, the vertices A to D are placed in an Array, and each vertex in the array has its index written right next to it.

Each vertex in the Array has a pointer to a Linked List that represents that vertex's edges. More specifically, the Linked List contains the indexes to the adjacent (neighbor) vertices.

So for example, vertex A has a link to a Linked List with values 3, 1, and 2. These values are the indexes to A's adjacent vertices D, B, and C.

An Adjacency List can also represent a directed and weighted Graph, like this:

In the Adjacency List above, vertices are stored in an Array. Each vertex has a pointer to a Linked List with edges stored as i,w , where i is the index of the vertex the edge goes to, and w is the weight of that edge.

Node D for example, has a pointer to a Linked List with an edge to vertex A. The values 0,4 means that vertex D has an edge to vertex on index 0 (vertex A), and the weight of that edge is 4 .

DSA Exercises

Test yourself with exercises.

How can the Graph below be described?

Start the Exercise

COLOR PICKER

Contact Sales

If you want to use W3Schools services as an educational institution, team or enterprise, send us an e-mail: [email protected]

Report Error

If you want to report an error, or if you want to make a suggestion, send us an e-mail: [email protected]

Top Tutorials

Top references, top examples, get certified.

• Heap Data Structure
• Implementing Heaps
• B Trees (M-way Tree)
• Introduction to Graphs
• Graph Representations

Graph Representations - Adjacency Matrix and List

There are two ways in which we represent graphs, these are:

Adjacency Matrix

Adjacency list.

Both these have their advantages and disadvantages. In this tutorial, we will cover both of these graph representation along with how to implement them.

Adjacency matrix representation makes use of a matrix (table) where the first row and first column of the matrix denote the nodes (vertices) of the graph. The rest of the cells contains either 0 or 1 (can contain an associated weight w if it is a weighted graph).

Each row X column intersection points to a cell and the value of that cell will help us in determining that whether the vertex denoted by the row and the vertex denoted by the column are connected or not. If the value of the cell for v1 X v2 is equal to 1, then we can conclude that these two vertices v1 and v2 are connected by an edge, else they aren't connected at all.

Consider the given graph below:

The graph shown above is an undirected one and the adjacency matrix for the same looks as:

The above matrix is the adjacency matrix representation of the graph shown above. If we look closely, we can see that the matrix is symmetric. Now let's see how the adjacency matrix changes for a directed graph.

For the directed graph shown above the adjacency matrix will look something like this:

Implementation of Adjacency Matrix

The structure ( constructor in Java ) for the adjacency matrix will look something like this:

It should also be noted that we have two class-level variables, like:

We have a constructor above named AdjacencyMatrix which takes the count of the number of the vertices that are present in the graph and then assigns our global vertex variable that value and also creates a 2D matrix of the same size. Now since our structure part is complete, we are simply left with adding the edges together, and the way we do that is:

In the above addEdge function we also assigned 1 for the direction from the destination to the start node, as in this code we looked at the example of the undirected graph, in which the relationship is a two-way process. If it had been a directed graph, then we can simply make this value equal to 0, and we would have a valid adjacency matrix.

Now the only thing left is to print the graph.

The entire code looks something like this:

The output of the above looks like:

Adjacency Matrix : 0 1 0 0 1 0 1 0 0 1 0 1 0 0 1 0

In the adjacency list representation, we have an array of linked-list where the size of the array is the number of the vertex (nodes) present in the graph. Each vertex has its own linked-list that contains the nodes that it is connected to.

Consider the graph shown below:

The above graph is an undirected one and the Adjacency list for it looks like:

The first column contains all the vertices we have in the graph above and then each of these vertices contains a linked list that in turn contains the nodes that each vertex is connected to. For a directed graph the only change would be that the linked list will only contain the node on which the incident edge is present.

The above graph is a directed one and the Adjacency list for this looks like:

Implementation of Adjacency List

The structure (constructor in Java) for the adjacency list will look something like this:

The above constructor takes the number of vertices as an argument and then assigns the class level variable this value, and then we create an array of LinkedList of the size of the vertices present in the graph. Finally, we create an empty LinkedList for each item of this array of LinkedList.

Now we have laid the foundations and the only thing left is to add the edges together, we do that like this:

We are taking the vertices from which an edge starts and ends, and we are simply inserting the destination vertex in the LinkedList of the start vertex and vice-versa (as it is for the undirected graph).

Node 0 is connected to: 1 Node 1 is connected to: 2 0 Node 2 is connected to: 3 1 Node 3 is connected to: 2

• We learned how to represent the graphs in programming, via adjacency matrix and adjacency lists.
• ← Introduction to Graphs ← PREV
• Hash Table → NEXT →

EnjoyMathematics

Adjacency List and Adjacency Matrix Representation of Graph

Why is understanding the representation of graphs important? One of the key reasons is that it helps us efficiently model real-life graph problems based on various properties and constraints. In other words, several fundamental properties of graphs impact the choice of data structures used to represent them. So, let’s move forward to understand this idea!

Just like other data structures, we can represent graphs using sequential and list representations: Adjacency list and adjacency matrix . We can apply both representations to model directed and undirected graphs.

Adjacency List Representation of Graph

In the adjacency-list representation, we create an array Adj[V] of size V, where each array element represents a graph vertex, and the array index corresponds to the vertex itself. On the other side, for each vertex u, Adj[u] is a list (array or linked list) that contains all the vertices adjacent to vertex u. So, the elements within the list at Adj[u] represent vertices that share an edge with vertex u. In other words, for each vertex v in Adj[u], there is an edge (u, v) in the graph.

Now, let’s consider another insight: How does this representation differ for directed and undirected graphs? In a directed graph, every edge is unidirectional. So, for any directed edge (u, v), node v will only appear in the adjacency list of vertex u. On the other hand, in an undirected graph, every edge is bidirectional, i.e., if (u, v) is an undirected edge, then u appears in v’s adjacency list, and vice versa. So, what can be derived from this observation?

• In a directed graph, the sum of the lengths of all the adjacency lists is equal to the number of edges.
• In an undirected graph, the sum of the lengths of all the adjacency lists is equal to twice the number of edges.
• In the adjacency-list representation of both directed and undirected graphs, the overall space complexity to represent the graph G(V, E) = O(V) + O(E) = O(V + E).

We can also use adjacency lists to represent weighted graphs. For example, in a directed graph, we can simply store the weight w(u, v) of the edge (u, v) in vertex v within the adjacency list of vertex u. Overall, the adjacency-list representation is quite flexible, allowing us to modify it to implement various types of graphs.

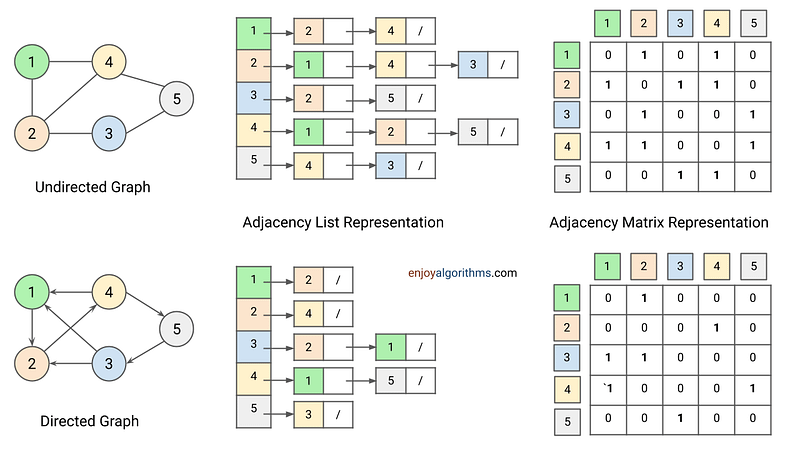
Adjacency Matrix Representation of Graph

For the adjacency-matrix representation of a graph G = (V, E), we assume that the vertices are numbered from 1, 2, …, V. So, the adjacency-matrix representation of a graph G consists of a V x V matrix A, such that A[u][v] = 1 if there is an edge between u and v, and A[u][v] = 0 if there is no edge between u and v.

Here are some observations:

• The adjacency matrix requires O(V²) memory, independent of the number of edges in the graph.
• In an undirected graph, since (u, v) and (v, u) represent the same edge, the adjacency matrix representation of the undirected graph is symmetrical along the main diagonal. So the adjacency matrix A of an undirected graph is its own transpose. Can we use this idea to optimize the space required to represent undirected graph? Think and explore.
• It may use a large amount of space for graphs with many vertices and relatively few edges. Suppose there is a 20 x 25 street in your city. This will give you 500 vertices and 1,000 edges, as each vertex neighbours four other vertices, and each edge is shared between two vertices. So in this scenario, the adjacency matrix would have 500 × 500 = 25,000 cells, almost all of them empty!
• We can also use an adjacency matrix to represent a weighted graph. For example, we can simply store the weight w(u, v) of the edge (u, v) in row u and column v of the adjacency matrix. If an edge does not exist, we can store a NIL value in its corresponding matrix entry.

Adjacency matrix vs Adjacency list

Now, the critical question is: When should we use an adjacency list, and when should we use an adjacency matrix? Selecting the right graph data structure can have a significant impact on performance. Let’s explore this critical comparison.

In an undirected graph with V vertices, the maximum possible number of edges that can exist is V * (V — 1) / 2, which is O(V²). Here, we are assuming that there are no self-loops or parallel edges. So, the choice between an adjacency list and an adjacency matrix depends on the density of the graph.

• If the graph is sparse i.e. the number of edges E is much less than the number of vertices V, or E is close to V, we prefer an adjacency list because it will take O(V + E) memory. This helps us store only the existing edges in a memory-efficient manner. On the other hand, if we use an adjacency matrix for a sparse graph, it will unnecessarily use O(V²) space.
• We prefer an adjacency-matrix representation when the graph is dense, i.e., the number of edges E is much larger than V, or when we need to quickly determine if there is an edge connecting two given vertices. On the other hand, the adjacency list provides no quicker way to determine whether a given edge (u, v) is present in the graph. For this, we need to traverse the length of the adjacency list of node u in the worst case.
• Although the adjacency-list representation is asymptotically at least as space-efficient as the adjacency-matrix representation, adjacency matrices are simpler, and so we may prefer them when graphs are reasonably small. Moreover, adjacency matrices carry a further advantage for unweighted graphs: they require only one bit per entry.

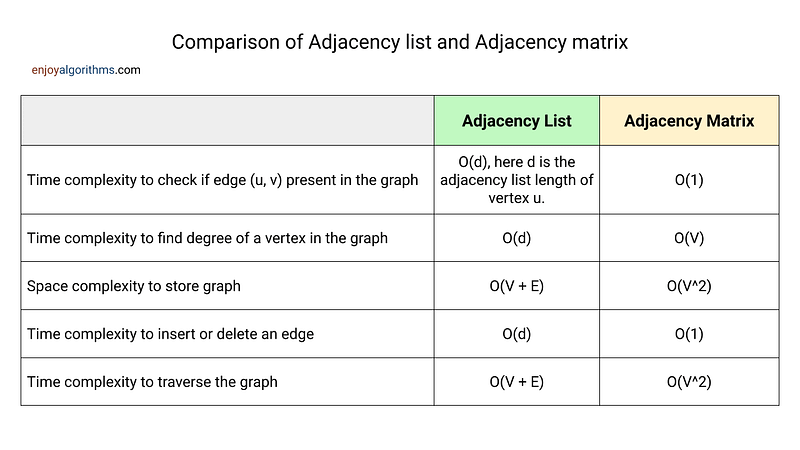
As we can see from the above table, adjacency lists make it harder to verify whether a given edge (u, v) exists, as we must search through the appropriate list to find the edge. However, it is easy to design graph algorithms that avoid the need for such queries. For example, we can explore all the edges of the graph in one pass via a breadth-first or depth-first traversal and perform operations on the current edge as we visit it. In this way, adjacency lists are the right data structure for most graph applications.

Basic Graph Operations

Adjacency list representation using vector or array list.

In this code, the Graph class uses an adjacency list representation for the graph and supports various operations such as adding edges, deleting edges and storing information about the vertices and edges.

Adjacency list representation using linked list

Adjacency matrix representation, critical idea to think.

• Is there another way to represent a graph?
• Which graph algorithms work perfectly with an adjacency list?
• Which graph algorithms work perfectly with an adjacency matrix?
• The adjacency matrix representation of an undirected graph is symmetrical in terms of the matrix diagonal. Can we use this idea to optimize space?
• Apart from degree and weight, what other types of additional information can we store inside the edges or nodes of a graph?

Enjoy learning, enjoy algorithms!

Share Your Insights

Don’t fill this out if you’re human:

More from EnjoyAlgorithms

Self-paced courses and blogs, coding interview, machine learning, system design, oop concepts, our newsletter.

Subscribe to get well designed content on data structure and algorithms, machine learning, system design, object orientd programming and math.

©2023 Code Algorithms Pvt. Ltd.

All rights reserved.

Learn Python practically and Get Certified .

Popular Tutorials

Popular examples, reference materials, certification courses.

Created with over a decade of experience and thousands of feedback.

DSA Introduction

• Getting Started with DSA
• What is an algorithm?
• Data Structure and Types
• Why learn DSA?
• Asymptotic Notations
• Master Theorem
• Divide and Conquer Algorithm

Data Structures (I)

• Types of Queue
• Circular Queue
• Priority Queue

Data Structures (II)

• Linked List
• Linked List Operations
• Types of Linked List
• Heap Data Structure
• Fibonacci Heap
• Decrease Key and Delete Node Operations on a Fibonacci Heap

Tree based DSA (I)

• Tree Data Structure
• Tree Traversal
• Binary Tree
• Full Binary Tree
• Perfect Binary Tree
• Complete Binary Tree
• Balanced Binary Tree
• Binary Search Tree

Tree based DSA (II)

• Insertion in a B-tree
• Deletion from a B-tree
• Insertion on a B+ Tree
• Deletion from a B+ Tree
• Red-Black Tree
• Red-Black Tree Insertion
• Red-Black Tree Deletion

Graph based DSA

• Graph Data Structure
• Spanning Tree
• Strongly Connected Components

Adjacency Matrix

Adjacency List

• DFS Algorithm
• Breadth-first Search
• Bellman Ford's Algorithm

Sorting and Searching Algorithms

• Bubble Sort
• Selection Sort
• Insertion Sort
• Counting Sort
• Bucket Sort
• Linear Search
• Binary Search

Greedy Algorithms

• Greedy Algorithm
• Ford-Fulkerson Algorithm
• Dijkstra's Algorithm
• Kruskal's Algorithm
• Prim's Algorithm
• Huffman Coding
• Dynamic Programming
• Floyd-Warshall Algorithm
• Longest Common Sequence

Other Algorithms

• Backtracking Algorithm
• Rabin-Karp Algorithm

DSA Tutorials

Graph Data Stucture

Depth First Search (DFS)

Breadth first search

An adjacency matrix is a way of representing a graph as a matrix of booleans (0's and 1's). A finite graph can be represented in the form of a square matrix on a computer, where the boolean value of the matrix indicates if there is a direct path between two vertices.

For example, we have a graph below.

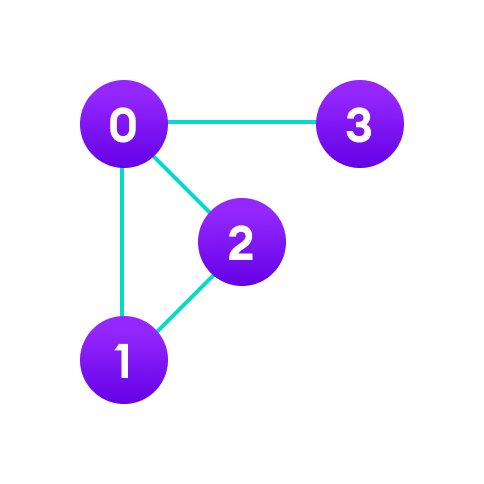
We can represent this graph in matrix form like below.

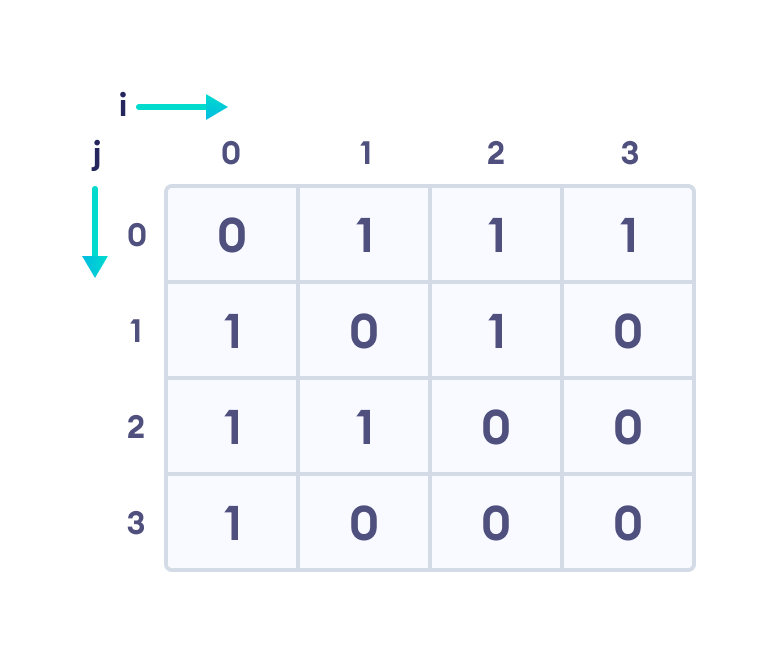
Each cell in the above table/matrix is represented as A ij , where i and j are vertices. The value of A ij is either 1 or 0 depending on whether there is an edge from vertex i to vertex j .

If there is a path from i to j , then the value of A ij is 1 otherwise its 0. For instance, there is a path from vertex 1 to vertex 2, so A 12 is 1 and there is no path from vertex 1 to 3, so A 13 is 0.

In case of undirected graphs, the matrix is symmetric about the diagonal because of every edge (i,j) , there is also an edge (j,i) .

• Pros of Adjacency Matrix
• The basic operations like adding an edge, removing an edge, and checking whether there is an edge from vertex i to vertex j are extremely time efficient, constant time operations.
• If the graph is dense and the number of edges is large, an adjacency matrix should be the first choice. Even if the graph and the adjacency matrix is sparse, we can represent it using data structures for sparse matrices.
• The biggest advantage, however, comes from the use of matrices. The recent advances in hardware enable us to perform even expensive matrix operations on the GPU.
• By performing operations on the adjacent matrix, we can get important insights into the nature of the graph and the relationship between its vertices.
• Cons of Adjacency Matrix
• The VxV space requirement of the adjacency matrix makes it a memory hog. Graphs out in the wild usually don't have too many connections and this is the major reason why adjacency lists are the better choice for most tasks.
• While basic operations are easy, operations like inEdges and outEdges are expensive when using the adjacency matrix representation.
• Adjacency Matrix Code in Python, Java, and C/C++

If you know how to create two-dimensional arrays, you also know how to create an adjacency matrix.

• Adjacency Matrix Applications
• Creating routing table in networks
• Navigation tasks

Table of Contents

• Introduction

Sorry about that.

Our premium learning platform, created with over a decade of experience and thousands of feedbacks .

Learn and improve your coding skills like never before.

• Interactive Courses
• Certificates
• 2000+ Challenges

Related Tutorials

DS & Algorithms

• Trending Categories

• Selected Reading
• UPSC IAS Exams Notes
• Developer's Best Practices
• Questions and Answers
• Effective Resume Writing
• HR Interview Questions
• Computer Glossary

Matrix Representation of Graphs

A graph can be represented using Adjacency Matrix way.

Adjacency Matrix

An Adjacency Matrix A[V][V] is a 2D array of size V × V where $V$ is the number of vertices in a undirected graph. If there is an edge between V x to V y then the value of A[V x ][V y ]=1 and A[V y ][V x ]=1, otherwise the value will be zero.

For a directed graph, if there is an edge between V x to V y , then the value of A[V x ][V y ]=1, otherwise the value will be zero.

Adjacency Matrix of an Undirected Graph

Let us consider the following undirected graph and construct the adjacency matrix −

Adjacency matrix of the above undirected graph will be −

Adjacency Matrix of a Directed Graph

Let us consider the following directed graph and construct its adjacency matrix −

Adjacency matrix of the above directed graph will be −

• Related Articles
• Representation of Graphs
• Convert Adjacency Matrix to Adjacency List Representation of Graph
• Add and Remove Vertex in Adjacency Matrix Representation of Graph
• Prim’s Algorithm (Simple Implementation for Adjacency Matrix Representation) in C++
• Basic Concepts of Graphs
• Application Of Linear Graphs
• Representation of fractions
• Isomorphism and Homeomorphism of graphs
• Bipartite Graphs
• Eulerian Graphs
• Hamiltonian Graphs
• Planar Graphs
• Successor Graphs
• Strongly Connected Graphs
• Speed Time Graphs

Kickstart Your Career

Get certified by completing the course

• Interview Problems on Graph
• Practice Graph
• MCQs on Graph
• Graph Tutorial
• Graph Representation
• Graph Properties
• Types of Graphs
• Graph Applications
• BFS on Graph
• DFS on Graph
• Graph VS Tree
• Transpose Graph
• Dijkstra's Algorithm
• Minimum Spanning Tree
• Prim’s Algorithm
• Topological Sorting
• Floyd Warshall Algorithm
• Strongly Connected Components
• Advantages & Disadvantages

Introduction to Graph Data Structure

Graph Data Structure is a non-linear data structure consisting of vertices and edges. It is useful in fields such as social network analysis, recommendation systems, and computer networks. In the field of sports data science, graph data structure can be used to analyze and understand the dynamics of team performance and player interactions on the field.

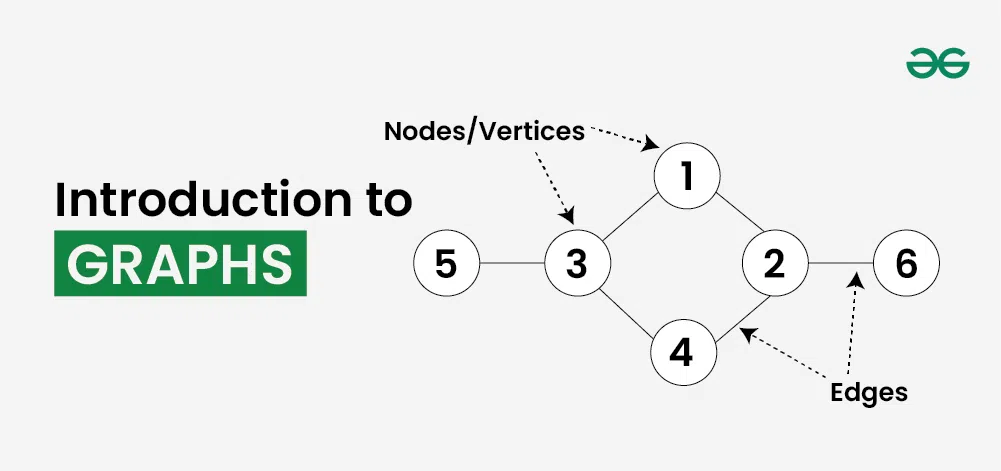
Table of Content

What is Graph Data Structure?

Components of graph data structure.

• Types Of Graph Data Structure
• Representation of Graph Data Structure
• Adjacency Matrix Representation of Graph Data Structure
• Adjacency List Representation of Graph
• Basic Operations on Graph Data Structure
• Difference between Tree and Graph
• Real-Life Applications of Graph Data Structure
• Advantages of Graph Data Structure
• Disadvantages of Graph Data Structure
• Frequently Asked Questions(FAQs) on Graph Data Structure

Graph is a non-linear data structure consisting of vertices and edges. The vertices are sometimes also referred to as nodes and the edges are lines or arcs that connect any two nodes in the graph. More formally a Graph is composed of a set of vertices( V ) and a set of edges( E ). The graph is denoted by G(V, E).

Imagine a game of football as a web of connections, where players are the nodes and their interactions on the field are the edges. This web of connections is exactly what a graph data structure represents, and it’s the key to unlocking insights into team performance and player dynamics in sports.

• Vertices: Vertices are the fundamental units of the graph. Sometimes, vertices are also known as vertex or nodes. Every node/vertex can be labeled or unlabelled.
• Edges: Edges are drawn or used to connect two nodes of the graph. It can be ordered pair of nodes in a directed graph. Edges can connect any two nodes in any possible way. There are no rules. Sometimes, edges are also known as arcs. Every edge can be labelled/unlabelled.

Types Of Graphs in Data Structure and Algorithms

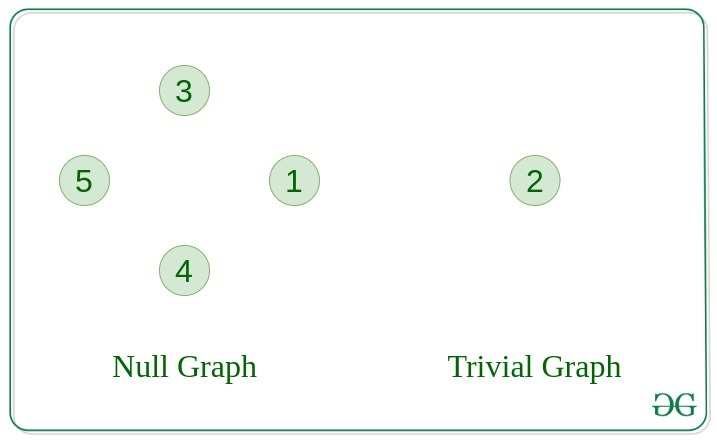
1. null graph.

A graph is known as a null graph if there are no edges in the graph.

2. Trivial Graph

3. Undirected Graph

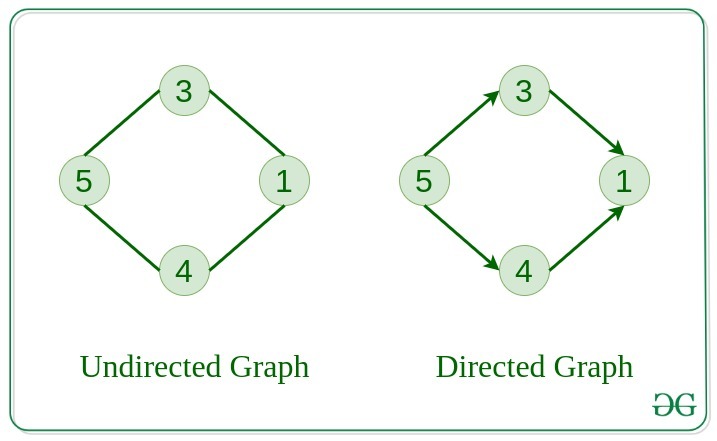
A graph in which edges do not have any direction. That is the nodes are unordered pairs in the definition of every edge. 

4. Directed Graph

A graph in which edge has direction. That is the nodes are ordered pairs in the definition of every edge.

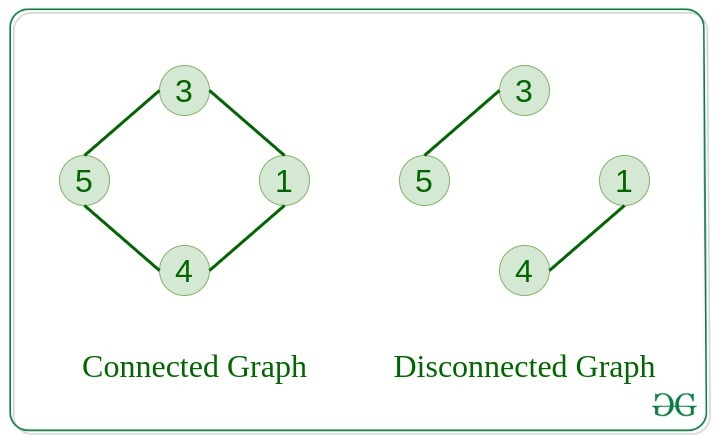
5. Connected Graph

The graph in which from one node we can visit any other node in the graph is known as a connected graph. 

6. Disconnected Graph

The graph in which at least one node is not reachable from a node is known as a disconnected graph.

7. Regular Graph

The graph in which the degree of every vertex is equal to K is called K regular graph.

8. Complete Graph

9. Cycle Graph

The graph in which the graph is a cycle in itself, the minimum value of degree of each vertex is 2. 

10. Cyclic Graph

A graph containing at least one cycle is known as a Cyclic graph.

11. Directed Acyclic Graph

A Directed Graph that does not contain any cycle. 

12. Bipartite Graph

A graph in which vertex can be divided into two sets such that vertex in each set does not contain any edge between them.

13. Weighted Graph

•   A graph in which the edges are already specified with suitable weight is known as a weighted graph. 
•  Weighted graphs can be further classified as directed weighted graphs and undirected weighted graphs. 

Representation of Graph Data Structure:

There are multiple ways to store a graph: The following are the most common representations.

• Adjacency Matrix
• Adjacency List

Adjacency Matrix Representation of Graph Data Structure:

In this method, the graph is stored in the form of the 2D matrix where rows and columns denote vertices. Each entry in the matrix represents the weight of the edge between those vertices. 

Below is the implementation of Graph Data Structure represented using Adjacency Matrix:

Adjacency List Representation of Graph:

This graph is represented as a collection of linked lists. There is an array of pointer which points to the edges connected to that vertex. 

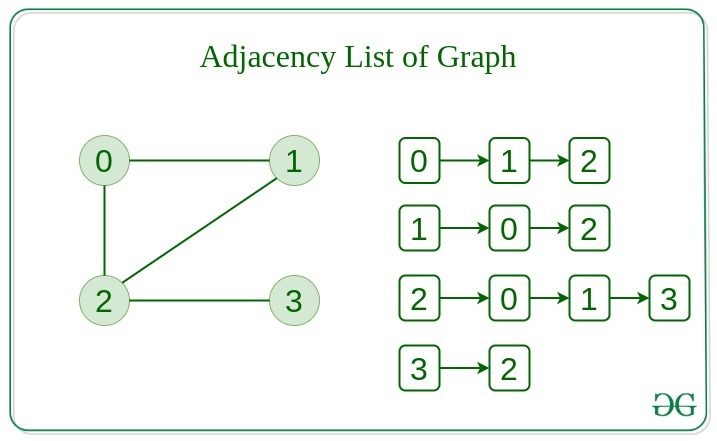
Below is the implementation of Graph Data Structure represented using Adjacency List:

Comparison between Adjacency Matrix and Adjacency List

When the graph contains a large number of edges then it is good to store it as a matrix because only some entries in the matrix will be empty. An algorithm such as Prim’s and Dijkstra adjacency matrix is used to have less complexity.

Basic Operations on Graph Data Structure:

Below are the basic operations on the graph:

• Add and Remove vertex in Adjacency List representation of Graph
• Add and Remove vertex in Adjacency Matrix representation of Graph
• Add and Remove Edge in Adjacency List representation of a Graph
• Add and Remove Edge in Adjacency Matrix representation of a Graph
• Searching in Graph Data Structure- Search an entity in the graph.
• Traversal of Graph Data Structure- Traversing all the nodes in the graph.

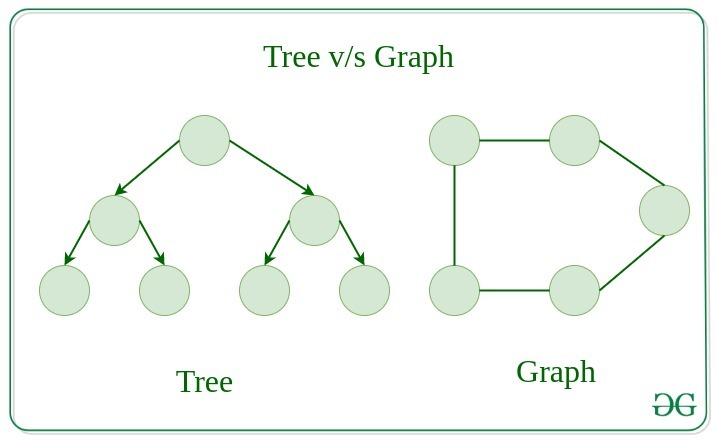
Difference between Tree and Graph:

Tree is a restricted type of Graph Data Structure, just with some more rules. Every tree will always be a graph but not all graphs will be trees. Linked List , Trees , and Heaps all are special cases of graphs. 

Real-Life Applications of Graph Data Structure:

Graph Data Structure has numerous real-life applications across various fields. Some of them are listed below:

• If we recall all the previous data structures that we have studied like array, linked list, tree, etc. All these had some restrictions on structure (mostly linear and tree hierarchical which means no loops). Graph allows random connections between nodes which is useful in many real world problems where do have restrictions of previous data structures.
• Used heavily in social networks. Everyone on the network is a vertex (or node) of the graph and if connected, then there is an edge. Now imagine all the features that you see, mutual friends, people that follow you, etc can seen as graph problems.
• Used to represent the topology of computer networks, such as the connections between routers and switches.
• Used to represent the connections between different places in a transportation network, such as roads and airports.
• Neural Networks: Vertices represent neurons and edges represent the synapses between them. Neural networks are used to understand how our brain works and how connections change when we learn. The human brain has about 10^11 neurons and close to 10^15 synapses.
• Compilers: Graph Data Structure is used extensively in compilers. They can be used for type inference, for so-called data flow analysis, register allocation, and many other purposes. They are also used in specialized compilers, such as query optimization in database languages.
• Robot planning: Vertices represent states the robot can be in and the edges the possible transitions between the states. Such graph plans are used, for example, in planning paths for autonomous vehicles.
• Dependencies in a software project (or any other type of project) can be seen as graph and generating a sequence to solve all tasks before dependents is a standard graph topological sorting algorithm.
• For optimizing the cost of connecting all locations of a network. For example, minimizing wire length in a wired network to make sure all devices are connected is a standard Graph problem called Minimum Spanning Tree.

Advantages of Graph Data Structure:

• Graph Data Structure used to represent a wide range of relationships as we do not have any restrictions like previous data structures (Tree cannot have loops and have to be hierarchical. Arrays, Linked List, etc are linear)
• They can be used to model and solve a wide range of problems, including pathfinding, data clustering, network analysis, and machine learning.
• Any real world problem where we certain set of items and relations between them can be easily modeled as a graph and a lot of standard graph algorithms like BFS, DFS, Spanning Tree, Shortest Path, Topological Sorting and Strongly Connected
• Graph Data Structure can be used to represent complex data structures in a simple and intuitive way, making them easier to understand and analyze.

Disadvantages of Graph Data Structure:

• Graph Data Structure can be complex and difficult to understand, especially for people who are not familiar with graph theory or related algorithms.
• Creating and manipulating graphs can be computationally expensive, especially for very large or complex graphs.
• Graph algorithms can be difficult to design and implement correctly, and can be prone to bugs and errors.
• Graph Data Structure can be difficult to visualize and analyze, especially for very large or complex graphs, which can make it challenging to extract meaningful insights from the data.

Frequently Asked Questions(FAQs) on Graph Data Structure:

1. what is a graph.

A graph is a data structure consisting of a set of vertices (nodes) and a set of edges that connect pairs of vertices.

2. What are the different types of Graph Data Structure?

Graph Data Structure can be classified into various types based on properties such as directionality of edges (directed or undirected), presence of cycles (acyclic or cyclic), and whether multiple edges between the same pair of vertices are allowed (simple or multigraph).

3. What are the applications of Graph Data Structure?

Graph Data Structure has numerous applications in various fields, including social networks, transportation networks, computer networks, recommendation systems, biology, chemistry, and more.

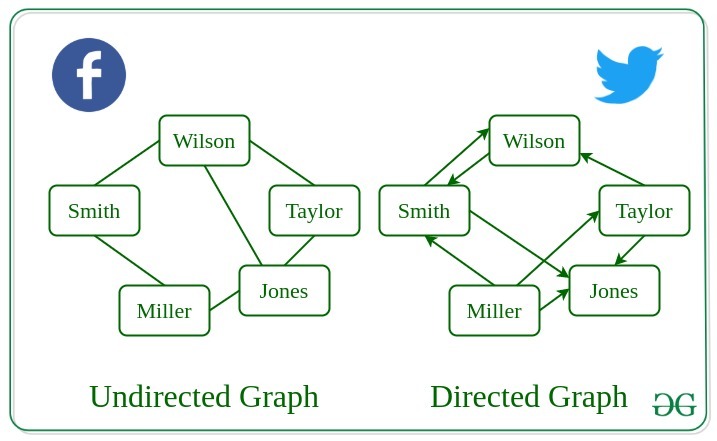
4. What is the difference between a directed graph and an undirected graph?

In an undirected graph, edges have no direction, meaning they represent symmetric relationships between vertices. In a directed graph (or digraph), edges have a direction, indicating a one-way relationship between vertices.

5. What is a weighted graph?

A weighted graph is a graph in which each edge is assigned a numerical weight or cost. These weights can represent distances, costs, or any other quantitative measure associated with the edges.

6. What is the degree of a vertex in a graph?

The degree of a vertex in a graph is the number of edges incident to that vertex. In a directed graph, the indegree of a vertex is the number of incoming edges, and the outdegree is the number of outgoing edges.

7. What is a path in a graph?

A path in a graph is a sequence of vertices connected by edges. The length of a path is the number of edges it contains.

8. What is a cycle in a graph?

A cycle in a graph is a path that starts and ends at the same vertex, traversing a sequence of distinct vertices and edges in between.

9. What are spanning trees and minimum spanning trees?

A spanning tree of a graph is a subgraph that is a tree and includes all the vertices of the original graph. A minimum spanning tree (MST) is a spanning tree with the minimum possible sum of edge weights.

10. What algorithms are commonly used to traverse or search Graph Data Structure?

Common graph traversal algorithms include depth-first search (DFS) and breadth-first search (BFS). These algorithms are used to explore or visit all vertices in a graph, typically starting from a specified vertex. Other algorithms, such as Dijkstra’s algorithm and Bellman-Ford algorithm, are used for shortest path finding.

More Resources of Graph:

• Recent Articles on Graph
• Practice problems on Graph
• Algorithms on Graphs

Similar Reads

• Data Structures

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Data Structures

Topics list.

• Introduction to Algorithms
• Performance Analysis
• Space Complexity
• Time Complexity
• Asymptotic Notations
• Linear & Non-Linear Data Structures
• Single Linked List
• Circular Linked List
• Double Linked List
• Sparse Matrix
• Stack Using Array
• Stack Using Linked List
• Expressions
• Infix to Postfix
• Postfix Evaluation
• Queue Using Array
• Queue Using Linked List
• Circular Queue
• Double Ended Queue
• Tree - Terminology
• Tree Representations
• Binary Tree
• Binary Tree Representations
• Binary Tree Traversals
• Threaded Binary Trees
• Max Priority Queue
• Introduction to Graphs

Graph Representations

• Graph Traversal - DFS
• Graph Traversal - BFS
• Linear Search
• Binary Search
• Insertion Sort
• Selection Sort
• Comparison of Sorting Methods
• Binary Search Tree
• Red - Black Trees
• Splay Trees
• Comparison of Search Trees
• Knuth-Morris-Pratt Algorithm

Graph data structure is represented using following representations...

Adjacency Matrix

Incidence matrix, adjacency list.

In this representation, the graph is represented using a matrix of size total number of vertices by a total number of vertices. That means a graph with 4 vertices is represented using a matrix of size 4X4. In this matrix, both rows and columns represent vertices. This matrix is filled with either 1 or 0. Here, 1 represents that there is an edge from row vertex to column vertex and 0 represents that there is no edge from row vertex to column vertex. For example, consider the following undirected graph representation...

Directed graph representation...

In this representation, the graph is represented using a matrix of size total number of vertices by a total number of edges. That means graph with 4 vertices and 6 edges is represented using a matrix of size 4X6. In this matrix, rows represent vertices and columns represents edges. This matrix is filled with 0 or 1 or -1. Here, 0 represents that the row edge is not connected to column vertex, 1 represents that the row edge is connected as the outgoing edge to column vertex and -1 represents that the row edge is connected as the incoming edge to column vertex. For example, consider the following directed graph representation...

In this representation, every vertex of a graph contains list of its adjacent vertices. For example, consider the following directed graph representation implemented using linked list...

This representation can also be implemented using an array as follows..

Website designed by Rajinikanth B