how to generate null and alternative hypothesis

How to Write a Null Hypothesis (5 Examples)

A hypothesis test uses sample data to determine whether or not some claim about a population parameter is true.

Whenever we perform a hypothesis test, we always write a null hypothesis and an alternative hypothesis, which take the following forms:

H 0 (Null Hypothesis): Population parameter =,  ≤, ≥ some value

H A  (Alternative Hypothesis): Population parameter <, >, ≠ some value

Note that the null hypothesis always contains the equal sign .

We interpret the hypotheses as follows:

Null hypothesis: The sample data provides no evidence to support some claim being made by an individual.

Alternative hypothesis: The sample data  does provide sufficient evidence to support the claim being made by an individual.

For example, suppose it’s assumed that the average height of a certain species of plant is 20 inches tall. However, one botanist claims the true average height is greater than 20 inches.

To test this claim, she may go out and collect a random sample of plants. She can then use this sample data to perform a hypothesis test using the following two hypotheses:

H 0 : μ ≤ 20 (the true mean height of plants is equal to or even less than 20 inches)

H A : μ > 20 (the true mean height of plants is greater than 20 inches)

If the sample data gathered by the botanist shows that the mean height of this species of plants is significantly greater than 20 inches, she can reject the null hypothesis and conclude that the mean height is greater than 20 inches.

Read through the following examples to gain a better understanding of how to write a null hypothesis in different situations.

Example 1: Weight of Turtles

A biologist wants to test whether or not the true mean weight of a certain species of turtles is 300 pounds. To test this, he goes out and measures the weight of a random sample of 40 turtles.

Here is how to write the null and alternative hypotheses for this scenario:

H 0 : μ = 300 (the true mean weight is equal to 300 pounds)

H A : μ ≠ 300 (the true mean weight is not equal to 300 pounds)

Example 2: Height of Males

It’s assumed that the mean height of males in a certain city is 68 inches. However, an independent researcher believes the true mean height is greater than 68 inches. To test this, he goes out and collects the height of 50 males in the city.

H 0 : μ ≤ 68 (the true mean height is equal to or even less than 68 inches)

H A : μ > 68 (the true mean height is greater than 68 inches)

Example 3: Graduation Rates

A university states that 80% of all students graduate on time. However, an independent researcher believes that less than 80% of all students graduate on time. To test this, she collects data on the proportion of students who graduated on time last year at the university.

H 0 : p ≥ 0.80 (the true proportion of students who graduate on time is 80% or higher)

H A : μ < 0.80 (the true proportion of students who graduate on time is less than 80%)

Example 4: Burger Weights

A food researcher wants to test whether or not the true mean weight of a burger at a certain restaurant is 7 ounces. To test this, he goes out and measures the weight of a random sample of 20 burgers from this restaurant.

H 0 : μ = 7 (the true mean weight is equal to 7 ounces)

H A : μ ≠ 7 (the true mean weight is not equal to 7 ounces)

Example 5: Citizen Support

A politician claims that less than 30% of citizens in a certain town support a certain law. To test this, he goes out and surveys 200 citizens on whether or not they support the law.

H 0 : p ≥ .30 (the true proportion of citizens who support the law is greater than or equal to 30%)

H A : μ < 0.30 (the true proportion of citizens who support the law is less than 30%)

Additional Resources

Introduction to Hypothesis Testing Introduction to Confidence Intervals An Explanation of P-Values and Statistical Significance

Featured Posts

Hey there. My name is Zach Bobbitt. I have a Masters of Science degree in Applied Statistics and I’ve worked on machine learning algorithms for professional businesses in both healthcare and retail. I’m passionate about statistics, machine learning, and data visualization and I created Statology to be a resource for both students and teachers alike.  My goal with this site is to help you learn statistics through using simple terms, plenty of real-world examples, and helpful illustrations.

2 Replies to “How to Write a Null Hypothesis (5 Examples)”

you are amazing, thank you so much

Say I am a botanist hypothesizing the average height of daisies is 20 inches, or not? Does T = (ave – 20 inches) / √ variance / (80 / 4)? … This assumes 40 real measures + 40 fake = 80 n, but that seems questionable. Please advise.

Leave a Reply Cancel reply

Your email address will not be published. Required fields are marked *

Join the Statology Community

Sign up to receive Statology's exclusive study resource: 100 practice problems with step-by-step solutions. Plus, get our latest insights, tutorials, and data analysis tips straight to your inbox!

By subscribing you accept Statology's Privacy Policy.

Null and Alternative Hypothesis: Research Guidelines

• Icon Calendar 17 June 2024
• Icon Page 2753 words
• Icon Clock 13 min read

When undertaking a qualitative or quantitative research project, researchers must first formulate a research question, from which they develop their theories. By definition, an assumption is a prediction that a researcher makes about an actual research question and can either be affirmative or negative. In this case, writing a research question has three main components: variables (independent and dependent), a population sample, and the relation between these variables. To find null and alternative hypotheses, scholars identify a specific research question, determine the variables involved, and state H0 as no effect or difference and H1 or Ha as a significant effect or difference. When the prediction contradicts the research question, it is referred to as a null assumption. In short, an initial theory is a statement that implies there is no relationship between independent and dependent variables. Hence, researchers need to learn how to write a good null and alternative hypothesis to present quality studies.

General Aspects

Students with qualitative or quantitative research assignments must learn how to formulate and write good research questions and proposition statements. In essence, hypothesis testing is a statistical method used to determine if there is enough evidence to reject an initial theory and support an alternative assumption based on sample data. By definition, a research proposition is an assumption or prediction that a scholar makes before undertaking an experimental investigation. Basically, academic standards require such a prediction to be a precise and testable statement, meaning that researchers must prove or disapprove of it in the course of their assignment and provide alternatives if possible. In this case, the main components of a typical research assumption are variables (independent and dependent), a population sample, and the relation between these variables. To formulate a null hypothesis (H0) in quantitative research, researchers state there is no effect or difference between variables (e.g., µ1 = µ2), and, for an alternative hypothesis (H1 or Ha), they posit there is a significant effect or difference (e.g., µ1 ≠ µ2). Therefore, a research proposition is a prediction that scholars write about the relationship between two or more variables. In turn, a standard research inquiry is a particular process that seeks to answer a specific research question and, in the process, test a particular theory by confirming or disapproving it.

Types of Hypotheses

There are several types of hypotheses, including null, alternative, directional, and non-directional assumptions. Basically, a directional hypothesis is a prediction of how an independent variable affects a dependent variable. In contrast, a non-directional hypothesis predicts that an independent variable influences a dependent variable but does not specify how. Regardless of the type, all propositions are about predicting the relationship between independent and dependent variables. To write H0 (null assumption) and H1 or Ha (alternative prediction), researchers clearly state H0 as a central assumption of no effect or no difference (e.g., µ1 = µ2) and H1 or Ha as a secondary assumption of a significant effect or difference (e.g., µ1 ≠ µ2).

What Is a Null Hypothesis (H0) and Its Purpose

According to its definition, a null hypothesis is a foundational statement in statistical testing that posits there is no significant effect, relationship, or difference between groups or variables within a given study. In simple words, a null hypothesis, usually symbolized as “H0,” is a statement that contradicts an actual research theory (Watt & Collins, 2019). The main purpose of writing a null hypothesis is to provide a basis for comparison, allowing researchers to determine whether there is sufficient evidence to reject this assumption in favor of an alternative theory, which suggests a real effect or relationship. As such, it is a negative statement, indicating that there is no relationship or connection between independent and dependent variables (Harrison et al., 2020). By starting with a null proposition, researchers can also employ various statistical tests to evaluate an entire data, ensuring the objectivity of findings and minimizing their bias. The process helps to ensure the validity of scientific research, minimizing the likelihood of drawing incorrect conclusions from the data collected. Moreover, by testing an initial theory, researchers can determine whether the inquiry results are due to the chance or the effect of manipulating a dependent variable (McNulty, 2022). In most instances, a null assumption corresponds with an alternative theory, a positive statement that covers a relationship that exists between independent and dependent variables. Finally, it is highly recommended that researchers should write an alternative assumption first before a null proposition.

What Is an Alternative Hypothesis (H1 or Ha) and Its Purpose

According to its definition and opposite to a null assumption, an alternative hypothesis in research is another statement in statistical testing that suggests there is a significant effect, relationship, or difference between groups or variables in a given study. Basically, this statement contrasts with what a null theory posits, which asserts that no such effect or relationship exists (Baker, 2021). The main purpose of writing an alternative hypothesis is to guide researchers in testing and validating new theories or effects and determine whether the observed data can provide evidence against a null proposition. The process involves comparing observed results to what would be expected under a null assumption. When statistical tests provide enough evidence to reject an initial postulation, an alternative theory becomes true, indicating that the observed effect or relationship is likely real and not due to random variation (Jawlik, 2016). By framing their research around an alternative hypothesis, scientists can focus their investigations on discovering meaningful effects and relationships, thereby advancing knowledge and understanding in their study fields. Hence, writing good null and alternative hypotheses is important because they provide a structured framework for statistical testing, allowing researchers to objectively evaluate evidence and draw conclusions about the presence of significant effects or relationships in an entire data.

Null vs. Alternative Hypothesis Formats

Steps on how to write a good null and alternative hypothesis.

• Identify a Specific Research Question: Start with clearly defining a particular problem or phenomenon you want to study.
• Determine Key Variables: Identify independent and dependent variables involved in your study.
• State a Specific Null Hypothesis (H0): Formulate a concrete statement that suggests no effect, no difference, or no relationship between your variables. This is usually a statement of equality (e.g., µ1 = µ2).
• State a Clear Alternative Hypothesis (H1 or Ha): Formulate another statement that suggests a significant effect, difference, or relationship between your variables. This is usually a statement of inequality (e.g., µ1 ≠ µ2, µ1 > µ2, or µ1 < µ2).
• Means: H0: µ1 = µ2 vs. H1: µ1 ≠ µ2
• Proportions: H0: p1 = p2 vs. H1: p1 ≠ p2
• One-tailed test: If you are testing for a specific direction of effect (e.g., H1: µ1 > µ2).
• Two-tailed test: If you are testing for any difference, regardless of direction (e.g., H1: µ1 ≠ µ2).
• Consult Literature: Review existing research to see how similar or alternative theories have been formulated. This can provide guidance and ensure your expectations are aligned with standard practices in your field.
• Write in Simple Terms: Ensure both null and alternative theories are stated clearly and concisely, making them easy to understand.
• Review and Refine: Double-check your propositions for clarity and correctness. Make sure they are mutually exclusive and collectively exhaustive, covering all possible outcomes.
• Seek Feedback: Discuss your approaches with peers or advisors to ensure they are logical, relevant, and testable. Adjust as necessary based on their input.

Note: A null hypothesis is a specific statement assuming no effect or difference, while other hypotheses refer to general statements that include writing null and alternative hypotheses and proposing possible outcomes to be tested.

Written Examples of Research Questions With H0 and H1 Hypotheses

Before developing any study proposition, a researcher must formulate a specific research question. In this case, a research hypothesis is a broad, testable statement about the expected relationship between variables, while a statistical hypothesis specifically refers to writing null and alternative hypotheses used in statistical testing to validate or refute an initial study assumption (O’Donnell et al., 2023). Then, the next step is to transform this study question into a negative statement that claims the lack of a relationship between independent and dependent variables. Alternatively, researchers can change the question into a positive statement that includes a relationship that exists between the variables. In turn, this latter statement becomes an alternative hypothesis and is symbolized as H1 or Ha. Hence, some of the examples of research questions and hull and alternative hypotheses are as follows:

Research Question (RQ) 1: Do physical exercises help individuals to age gracefully?

• A Null Hypothesis (H0): Physical exercises are not a guarantee for graceful old age.
• An Alternative Hypothesis (H1): Engaging in physical exercises enables individuals to remain healthy and active into old age.

RQ 2: What are the implications of therapeutic interventions in the fight against substance abuse?

• H0: Therapeutic interventions are of no help in the fight against substance abuse.
• H1: Exposing individuals with substance abuse disorders to therapeutic interventions helps to control and even stop their addictions.

RQ 3: How do sexual orientation and gender identity affect the experiences of late adolescents in foster care?

• H0: Sexual orientation and gender identity have no effects on the experiences of late adolescents in foster care.
• H1: The reality of stereotypes in society makes sexual orientation and gender identity factors complicate the experiences of late adolescents in foster care.

RQ 4: Does income inequality contribute to crime in high-density urban areas?

• H0: There is no correlation between income inequality and incidences of crime in high-density urban areas.
• H1: The high crime rates in high-density urban areas are due to the incidence of income inequality in those areas.

RQ 5: Does placement in foster care impact individuals’ mental health?

• H0: There is no correlation between being in foster care and having mental health problems.
• H1: Individuals placed in foster care experience anxiety and depression at one point in their life.

RQ 6: Do assistive devices and technologies lessen the mobility challenges of older adults with a stroke?

• H0: Assistive devices and technologies do not provide any assistance to the mobility of older adults diagnosed with a stroke.
• H1: Assistive devices and technologies enhance the mobility of older adults diagnosed with a stroke.

RQ 7: Does race identity undermine classroom participation?

• H0: There is no correlation between racial identity and the ability to participate in classroom learning.
• H1: Students from racial minorities are not as active as white students in classroom participation.

RQ 8: Do high school grades determine future success?

• H0: There is no correlation between how one performs in high school and their success level in life.
• H1: Attaining high grades in high school positions one for greater success in the future personal and professional lives.

RQ 9: Does critical thinking predict academic achievement?

• H0: There is no correlation between critical thinking and academic achievement.
• H1: Being a critical thinker is a pathway to academic success.

RQ 10: What benefits does group therapy provide to victims of domestic violence?

• H0: Group therapy does not help victims of domestic violence because individuals prefer to hide rather than expose their shame.
• H1: Group therapy provides domestic violence victims with a platform to share their hurt and connect with others with similar experiences.

Symbols and Signs in Writing

Common Mistakes

• Ambiguity in Theories: Writing vague or unclear null and alternative assumptions.
• Directional vs. Non-Directional Confusion: Confusing one-tailed (directional) and two-tailed (non-directional) claims.
• Using Sample Statistics: Stating initial and alternative propositions in terms of sample statistics instead of population parameters.
• Overlapping Assumptions: Creating null and alternative statements that are not mutually exclusive.
• Testing Multiple Variables: Including multiple variables or conditions in a single theory.
• Misinterpreting a Null Proposition: Assuming an initial statement is what you want to prove.
• Incorrect Symbols and Signs: Using incorrect or inconsistent symbols and signs for writing null and alternative propositions.
• Ignoring Context: Writing initial and alternative theories that are not relevant to an assigned research question or context.
• Not Testable Hypotheses: Formulating null and alternative statements that are not testable with the available data or methods.
• Confusing Null and Alternative Hypotheses: Swapping the roles of null and alternative assumptions.

The formulation of research questions in qualitative and quantitative assignments helps students to develop a specific theory for their experiments. In this case, learning how to write a good null and alternative hypothesis helps students and researchers to make their research relevant. Basically, the difference between a null and alternative hypothesis is that the former contradicts an entire research question, while the latter affirms it. In short, an initial proposition is a negative statement relative to a particular research question, and an alternative theory is a positive assumption. Moreover, it is important to note that developing a null hypothesis at the beginning of the assignment is for prediction purposes. As such, the research work must answer a specific research question and confirm or disapprove of an initial proposition. Hence, some of the tips that students and researchers need to know when developing any theory include:

• Formulate a research question that specifies the relationship between an independent variable and a dependent variable.
• Develop an alternative assumption that says a relationship exists between the variables.
• Develop a null proposition that says a relationship does not exist between the variables.
• Conduct an experiment to answer a research question under analysis, which allows the confirmation of a disapproval of a null theory or considering alternative options.

Baker, L. (2021). Hypothesis testing: How to choose the correct test (Getting started with statistics) . Chi-Squared Innovations.

Harrison, A. J., McErlain-Naylor, S. A., Bradshaw, E. J., Dai, B., Nunome, H., Hughes, G. T. G., Kong, P. W., Vanwanseele, B., Vilas-Boas, J. P., & Fong, D. T. (2020). Recommendations for statistical analysis involving null hypothesis significance testing. Sports Biomechanics , 19 (5), 561–568. https://doi.org/10.1080/14763141.2020.1782555

Jawlik, A. (2016). Statistics from A to Z: Confusing concepts clarified . John Wiley & Sons, Inc.

McNulty, R. (2022). A logical analysis of null hypothesis significance testing using popular terminology. BMC Medical Research Methodology , 22 (1), 1–9. https://doi.org/10.1186/s12874-022-01696-5

O’Donnell, C. T., Fielding-Singh, V., & Vanneman, M. W. (2023). The art of the null hypothesis — Considerations for study design and scientific reporting. Journal of Cardiothoracic and Vascular Anesthesia , 37 (6), 867–869. https://doi.org/10.1053/j.jvca.2023.02.026

Watt, R., & Collins, E. (2019). Null hypothesis testing . SAGE Publications Ltd.

To Learn More, Read Relevant Articles

SAT Essay Examples With Explanations and Recommendations

• Icon Calendar 29 July 2020
• Icon Page 3990 words

How to Cite Lecture Notes in APA: Basic Guidelines

• Icon Calendar 27 July 2020
• Icon Page 2390 words

Have a thesis expert improve your writing

Check your thesis for plagiarism in 10 minutes, generate your apa citations for free.

• Knowledge Base
• Null and Alternative Hypotheses | Definitions & Examples

Null and Alternative Hypotheses | Definitions & Examples

Published on 5 October 2022 by Shaun Turney . Revised on 6 December 2022.

The null and alternative hypotheses are two competing claims that researchers weigh evidence for and against using a statistical test :

• Null hypothesis (H 0 ): There’s no effect in the population .
• Alternative hypothesis (H A ): There’s an effect in the population.

The effect is usually the effect of the independent variable on the dependent variable .

Table of contents

Answering your research question with hypotheses, what is a null hypothesis, what is an alternative hypothesis, differences between null and alternative hypotheses, how to write null and alternative hypotheses, frequently asked questions about null and alternative hypotheses.

The null and alternative hypotheses offer competing answers to your research question . When the research question asks “Does the independent variable affect the dependent variable?”, the null hypothesis (H 0 ) answers “No, there’s no effect in the population.” On the other hand, the alternative hypothesis (H A ) answers “Yes, there is an effect in the population.”

The null and alternative are always claims about the population. That’s because the goal of hypothesis testing is to make inferences about a population based on a sample . Often, we infer whether there’s an effect in the population by looking at differences between groups or relationships between variables in the sample.

You can use a statistical test to decide whether the evidence favors the null or alternative hypothesis. Each type of statistical test comes with a specific way of phrasing the null and alternative hypothesis. However, the hypotheses can also be phrased in a general way that applies to any test.

The null hypothesis is the claim that there’s no effect in the population.

If the sample provides enough evidence against the claim that there’s no effect in the population ( p ≤ α), then we can reject the null hypothesis . Otherwise, we fail to reject the null hypothesis.

Although “fail to reject” may sound awkward, it’s the only wording that statisticians accept. Be careful not to say you “prove” or “accept” the null hypothesis.

Null hypotheses often include phrases such as “no effect”, “no difference”, or “no relationship”. When written in mathematical terms, they always include an equality (usually =, but sometimes ≥ or ≤).

Examples of null hypotheses

The table below gives examples of research questions and null hypotheses. There’s always more than one way to answer a research question, but these null hypotheses can help you get started.

*Note that some researchers prefer to always write the null hypothesis in terms of “no effect” and “=”. It would be fine to say that daily meditation has no effect on the incidence of depression and p 1 = p 2 .

The alternative hypothesis (H A ) is the other answer to your research question . It claims that there’s an effect in the population.

Often, your alternative hypothesis is the same as your research hypothesis. In other words, it’s the claim that you expect or hope will be true.

The alternative hypothesis is the complement to the null hypothesis. Null and alternative hypotheses are exhaustive, meaning that together they cover every possible outcome. They are also mutually exclusive, meaning that only one can be true at a time.

Alternative hypotheses often include phrases such as “an effect”, “a difference”, or “a relationship”. When alternative hypotheses are written in mathematical terms, they always include an inequality (usually ≠, but sometimes > or <). As with null hypotheses, there are many acceptable ways to phrase an alternative hypothesis.

Examples of alternative hypotheses

The table below gives examples of research questions and alternative hypotheses to help you get started with formulating your own.

Null and alternative hypotheses are similar in some ways:

• They’re both answers to the research question
• They both make claims about the population
• They’re both evaluated by statistical tests.

However, there are important differences between the two types of hypotheses, summarized in the following table.

To help you write your hypotheses, you can use the template sentences below. If you know which statistical test you’re going to use, you can use the test-specific template sentences. Otherwise, you can use the general template sentences.

The only thing you need to know to use these general template sentences are your dependent and independent variables. To write your research question, null hypothesis, and alternative hypothesis, fill in the following sentences with your variables:

Does independent variable affect dependent variable ?

• Null hypothesis (H 0 ): Independent variable does not affect dependent variable .
• Alternative hypothesis (H A ): Independent variable affects dependent variable .

Test-specific

Once you know the statistical test you’ll be using, you can write your hypotheses in a more precise and mathematical way specific to the test you chose. The table below provides template sentences for common statistical tests.

Note: The template sentences above assume that you’re performing one-tailed tests . One-tailed tests are appropriate for most studies.

The null hypothesis is often abbreviated as H 0 . When the null hypothesis is written using mathematical symbols, it always includes an equality symbol (usually =, but sometimes ≥ or ≤).

The alternative hypothesis is often abbreviated as H a or H 1 . When the alternative hypothesis is written using mathematical symbols, it always includes an inequality symbol (usually ≠, but sometimes < or >).

A research hypothesis is your proposed answer to your research question. The research hypothesis usually includes an explanation (‘ x affects y because …’).

A statistical hypothesis, on the other hand, is a mathematical statement about a population parameter. Statistical hypotheses always come in pairs: the null and alternative hypotheses. In a well-designed study , the statistical hypotheses correspond logically to the research hypothesis.

Cite this Scribbr article

If you want to cite this source, you can copy and paste the citation or click the ‘Cite this Scribbr article’ button to automatically add the citation to our free Reference Generator.

Turney, S. (2022, December 06). Null and Alternative Hypotheses | Definitions & Examples. Scribbr. Retrieved 16 December 2024, from https://www.scribbr.co.uk/stats/null-and-alternative-hypothesis/

Is this article helpful?

Shaun Turney

Other students also liked, levels of measurement: nominal, ordinal, interval, ratio, the standard normal distribution | calculator, examples & uses, types of variables in research | definitions & examples.

Interested in teaching this course?

Lumen can help! Review our up-to-date Introduction to Statistics by clicking the link below. From there, you can request a demo and review the course materials in your Learning Management System (LMS).

Module 9: Hypothesis Testing With One Sample

Null and alternative hypotheses, learning outcomes.

• Describe hypothesis testing in general and in practice

The actual test begins by considering two  hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

H 0 : The null hypothesis: It is a statement about the population that either is believed to be true or is used to put forth an argument unless it can be shown to be incorrect beyond a reasonable doubt.

H a : The alternative hypothesis : It is a claim about the population that is contradictory to H 0 and what we conclude when we reject H 0 .

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make adecision. There are two options for a  decision . They are “reject H 0 ” if the sample information favors the alternative hypothesis or “do not reject H 0 ” or “decline to reject H 0 ” if the sample information is insufficient to reject the null hypothesis.

Mathematical Symbols Used in  H 0 and H a :

H 0 always has a symbol with an equal in it. H a never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

H 0 : No more than 30% of the registered voters in Santa Clara County voted in the primary election. p ≤ 30

H a : More than 30% of the registered voters in Santa Clara County voted in the primary election. p > 30

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

H 0 : The drug reduces cholesterol by 25%. p = 0.25

H a : The drug does not reduce cholesterol by 25%. p ≠ 0.25

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

H 0 : μ = 2.0

H a : μ ≠ 2.0

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 66 H a : μ __ 66

• H 0 : μ = 66
• H a : μ ≠ 66

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

H 0 : μ ≥ 5

H a : μ < 5

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : μ __ 45 H a : μ __ 45

• H 0 : μ ≥ 45
• H a : μ < 45

In an issue of U.S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

H 0 : p ≤ 0.066

H a : p > 0.066

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (=, ≠, ≥, <, ≤, >) for the null and alternative hypotheses. H 0 : p __ 0.40 H a : p __ 0.40

• H 0 : p = 0.40
• H a : p > 0.40

Concept Review

In a  hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we: Evaluate the null hypothesis , typically denoted with H 0 . The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality (=, ≤ or ≥) Always write the alternative hypothesis , typically denoted with H a or H 1 , using less than, greater than, or not equals symbols, i.e., (≠, >, or <). If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis. Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

H 0 and H a are contradictory.

Candela Citations

• OpenStax, Statistics, Null and Alternative Hypotheses. Provided by : OpenStax. Located at : http://cnx.org/contents/[email protected]:58/Introductory_Statistics . License : CC BY: Attribution
• Introductory Statistics . Authored by : Barbara Illowski, Susan Dean. Provided by : Open Stax. Located at : http://cnx.org/contents/[email protected] . License : CC BY: Attribution . License Terms : Download for free at http://cnx.org/contents/[email protected]
• Simple hypothesis testing | Probability and Statistics | Khan Academy. Authored by : Khan Academy. Located at : https://youtu.be/5D1gV37bKXY . License : All Rights Reserved . License Terms : Standard YouTube License

• PRO Courses Guides New Tech Help Pro Expert Videos About wikiHow Pro Upgrade Sign In
• EDIT Edit this Article
• EXPLORE Tech Help Pro About Us Random Article Quizzes Request a New Article Community Dashboard This Or That Game Forums Popular Categories Arts and Entertainment Artwork Books Movies Computers and Electronics Computers Phone Skills Technology Hacks Health Men's Health Mental Health Women's Health Relationships Dating Love Relationship Issues Hobbies and Crafts Crafts Drawing Games Education & Communication Communication Skills Personal Development Studying Personal Care and Style Fashion Hair Care Personal Hygiene Youth Personal Care School Stuff Dating All Categories Arts and Entertainment Finance and Business Home and Garden Relationship Quizzes Cars & Other Vehicles Food and Entertaining Personal Care and Style Sports and Fitness Computers and Electronics Health Pets and Animals Travel Education & Communication Hobbies and Crafts Philosophy and Religion Work World Family Life Holidays and Traditions Relationships Youth
• Browse Articles
• Learn Something New
• Quizzes Hot
• Happiness Hub
• This Or That Game
• Train Your Brain
• Explore More
• Support wikiHow
• About wikiHow
• Log in / Sign up
• Education and Communications
• College University and Postgraduate
• Academic Writing

Writing Null Hypotheses in Research and Statistics

Last Updated: October 31, 2024 Fact Checked

This article was co-authored by Joseph Quinones and by wikiHow staff writer, Jennifer Mueller, JD . Joseph Quinones is a Physics Teacher working at South Bronx Community Charter High School. Joseph specializes in astronomy and astrophysics and is interested in science education and science outreach, currently practicing ways to make physics accessible to more students with the goal of bringing more students of color into the STEM fields. He has experience working on Astrophysics research projects at the Museum of Natural History (AMNH). Joseph recieved his Bachelor's degree in Physics from Lehman College and his Masters in Physics Education from City College of New York (CCNY). He is also a member of a network called New York City Men Teach. There are 7 references cited in this article, which can be found at the bottom of the page. This article has been fact-checked, ensuring the accuracy of any cited facts and confirming the authority of its sources. This article has been viewed 33,402 times.

Are you working on a research project and struggling with how to write a null hypothesis? Well, you've come to the right place! Keep reading to learn everything you need to know about the null hypothesis, including a review of what it is, how it relates to your research question and your alternative hypothesis, as well as how to use it in different types of studies.

Things You Should Know

• Write a research null hypothesis as a statement that the studied variables have no relationship to each other, or that there's no difference between 2 groups.

• Adjust the format of your null hypothesis to match the statistical method you used to test it, such as using "mean" if you're comparing the mean between 2 groups.

What is a null hypothesis?

• Research hypothesis: States in plain language that there's no relationship between the 2 variables or there's no difference between the 2 groups being studied.
• Statistical hypothesis: States the predicted outcome of statistical analysis through a mathematical equation related to the statistical method you're using.

Examples of Null Hypotheses

Null Hypothesis vs. Alternative Hypothesis

• For example, your alternative hypothesis could state a positive correlation between 2 variables while your null hypothesis states there's no relationship. If there's a negative correlation, then both hypotheses are false.

• You need additional data or evidence to show that your alternative hypothesis is correct—proving the null hypothesis false is just the first step.
• In smaller studies, sometimes it's enough to show that there's some relationship and your hypothesis could be correct—you can leave the additional proof as an open question for other researchers to tackle.

How do I test a null hypothesis?

• Group means: Compare the mean of the variable in your sample with the mean of the variable in the general population. [6] X Research source
• Group proportions: Compare the proportion of the variable in your sample with the proportion of the variable in the general population. [7] X Research source
• Correlation: Correlation analysis looks at the relationship between 2 variables—specifically, whether they tend to happen together. [8] X Research source
• Regression: Regression analysis reveals the correlation between 2 variables while also controlling for the effect of other, interrelated variables. [9] X Research source

Templates for Null Hypotheses

• Research null hypothesis: There is no difference in the mean [dependent variable] between [group 1] and [group 2].

• Research null hypothesis: The proportion of [dependent variable] in [group 1] and [group 2] is the same.

• Research null hypothesis: There is no correlation between [independent variable] and [dependent variable] in the population.

• Research null hypothesis: There is no relationship between [independent variable] and [dependent variable] in the population.

Expert Q&A

You Might Also Like

Expert Interview

Thanks for reading our article! If you’d like to learn more about physics, check out our in-depth interview with Joseph Quinones .

• ↑ https://www.investopedia.com/terms/n/null_hypothesis.asp
• ↑ https://support.minitab.com/en-us/minitab/21/help-and-how-to/statistics/basic-statistics/supporting-topics/basics/null-and-alternative-hypotheses/
• ↑ https://www.ncbi.nlm.nih.gov/pmc/articles/PMC5635437/
• ↑ https://education.arcus.chop.edu/null-hypothesis-testing/
• ↑ https://online.stat.psu.edu/stat100/lesson/10/10.1
• ↑ https://online.stat.psu.edu/stat501/lesson/2/2.12
• ↑ https://sphweb.bumc.bu.edu/otlt/mph-modules/bs/bs704_hypothesistest-means-proportions/bs704_hypothesistest-means-proportions_print.html

About This Article

• Send fan mail to authors

Reader Success Stories

Dec 3, 2022

Did this article help you?

Featured Articles

Trending Articles

Watch Articles

• Terms of Use
• Privacy Policy
• Do Not Sell or Share My Info
• Not Selling Info

wikiHow Tech Help Pro:

Develop the tech skills you need for work and life

Our websites may use cookies to personalize and enhance your experience. By continuing without changing your cookie settings, you agree to this collection. For more information, please see our University Websites Privacy Notice .

Neag School of Education

Educational Research Basics by Del Siegle

Null and alternative hypotheses.

Converting research questions to hypothesis is a simple task. Take the questions and make it a positive statement that says a relationship exists (correlation studies) or a difference exists between the groups (experiment study) and you have the alternative hypothesis. Write the statement such that a relationship does not exist or a difference does not exist and you have the null hypothesis. You can reverse the process if you have a hypothesis and wish to write a research question.

When you are comparing two groups, the groups are the independent variable. When you are testing whether something affects something else, the cause is the independent variable. The independent variable is the one you manipulate.

Teachers given higher pay will have more positive attitudes toward children than teachers given lower pay. The first step is to ask yourself “Are there two or more groups being compared?” The answer is “Yes.” What are the groups? Teachers who are given higher pay and teachers who are given lower pay. The independent variable is teacher pay. The dependent variable (the outcome) is attitude towards school.

You could also approach is another way. “Is something causing something else?” The answer is “Yes.”  What is causing what? Teacher pay is causing attitude towards school. Therefore, teacher pay is the independent variable (cause) and attitude towards school is the dependent variable (outcome).

By tradition, we try to disprove (reject) the null hypothesis. We can never prove a null hypothesis, because it is impossible to prove something does not exist. We can disprove something does not exist by finding an example of it. Therefore, in research we try to disprove the null hypothesis. When we do find that a relationship (or difference) exists then we reject the null and accept the alternative. If we do not find that a relationship (or difference) exists, we fail to reject the null hypothesis (and go with it). We never say we accept the null hypothesis because it is never possible to prove something does not exist. That is why we say that we failed to reject the null hypothesis, rather than we accepted it.

Del Siegle, Ph.D. Neag School of Education – University of Connecticut [email protected] www.delsiegle.com

• school Campus Bookshelves
• menu_book Bookshelves
• perm_media Learning Objects
• login Login
• how_to_reg Request Instructor Account
• hub Instructor Commons

Margin Size

• Download Page (PDF)
• Download Full Book (PDF)
• Periodic Table
• Physics Constants
• Scientific Calculator
• Reference & Cite
• Tools expand_more
• Readability

selected template will load here

This action is not available.

9.1: Null and Alternative Hypotheses

• Last updated
• Save as PDF
• Page ID 23459

\( \newcommand{\vecs}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vecd}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash {#1}}} \)

\( \newcommand{\id}{\mathrm{id}}\) \( \newcommand{\Span}{\mathrm{span}}\)

( \newcommand{\kernel}{\mathrm{null}\,}\) \( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\) \( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\) \( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\inner}[2]{\langle #1, #2 \rangle}\)

\( \newcommand{\Span}{\mathrm{span}}\)

\( \newcommand{\id}{\mathrm{id}}\)

\( \newcommand{\kernel}{\mathrm{null}\,}\)

\( \newcommand{\range}{\mathrm{range}\,}\)

\( \newcommand{\RealPart}{\mathrm{Re}}\)

\( \newcommand{\ImaginaryPart}{\mathrm{Im}}\)

\( \newcommand{\Argument}{\mathrm{Arg}}\)

\( \newcommand{\norm}[1]{\| #1 \|}\)

\( \newcommand{\Span}{\mathrm{span}}\) \( \newcommand{\AA}{\unicode[.8,0]{x212B}}\)

\( \newcommand{\vectorA}[1]{\vec{#1}}      % arrow\)

\( \newcommand{\vectorAt}[1]{\vec{\text{#1}}}      % arrow\)

\( \newcommand{\vectorB}[1]{\overset { \scriptstyle \rightharpoonup} {\mathbf{#1}} } \)

\( \newcommand{\vectorC}[1]{\textbf{#1}} \)

\( \newcommand{\vectorD}[1]{\overrightarrow{#1}} \)

\( \newcommand{\vectorDt}[1]{\overrightarrow{\text{#1}}} \)

\( \newcommand{\vectE}[1]{\overset{-\!-\!\rightharpoonup}{\vphantom{a}\smash{\mathbf {#1}}}} \)

The actual test begins by considering two hypotheses . They are called the null hypothesis and the alternative hypothesis . These hypotheses contain opposing viewpoints.

\(H_0\): The null hypothesis: It is a statement of no difference between the variables—they are not related. This can often be considered the status quo and as a result if you cannot accept the null it requires some action.

\(H_a\): The alternative hypothesis: It is a claim about the population that is contradictory to \(H_0\) and what we conclude when we reject \(H_0\). This is usually what the researcher is trying to prove.

Since the null and alternative hypotheses are contradictory, you must examine evidence to decide if you have enough evidence to reject the null hypothesis or not. The evidence is in the form of sample data.

After you have determined which hypothesis the sample supports, you make a decision. There are two options for a decision. They are "reject \(H_0\)" if the sample information favors the alternative hypothesis or "do not reject \(H_0\)" or "decline to reject \(H_0\)" if the sample information is insufficient to reject the null hypothesis.

\(H_{0}\) always has a symbol with an equal in it. \(H_{a}\) never has a symbol with an equal in it. The choice of symbol depends on the wording of the hypothesis test. However, be aware that many researchers (including one of the co-authors in research work) use = in the null hypothesis, even with > or < as the symbol in the alternative hypothesis. This practice is acceptable because we only make the decision to reject or not reject the null hypothesis.

Example \(\PageIndex{1}\)

• \(H_{0}\): No more than 30% of the registered voters in Santa Clara County voted in the primary election. \(p \leq 30\)
• \(H_{a}\): More than 30% of the registered voters in Santa Clara County voted in the primary election. \(p > 30\)

Exercise \(\PageIndex{1}\)

A medical trial is conducted to test whether or not a new medicine reduces cholesterol by 25%. State the null and alternative hypotheses.

• \(H_{0}\): The drug reduces cholesterol by 25%. \(p = 0.25\)
• \(H_{a}\): The drug does not reduce cholesterol by 25%. \(p \neq 0.25\)

Example \(\PageIndex{2}\)

We want to test whether the mean GPA of students in American colleges is different from 2.0 (out of 4.0). The null and alternative hypotheses are:

• \(H_{0}: \mu = 2.0\)
• \(H_{a}: \mu \neq 2.0\)

Exercise \(\PageIndex{2}\)

We want to test whether the mean height of eighth graders is 66 inches. State the null and alternative hypotheses. Fill in the correct symbol \((=, \neq, \geq, <, \leq, >)\) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 66\)
• \(H_{a}: \mu \_ 66\)
• \(H_{0}: \mu = 66\)
• \(H_{a}: \mu \neq 66\)

Example \(\PageIndex{3}\)

We want to test if college students take less than five years to graduate from college, on the average. The null and alternative hypotheses are:

• \(H_{0}: \mu \geq 5\)
• \(H_{a}: \mu < 5\)

Exercise \(\PageIndex{3}\)

We want to test if it takes fewer than 45 minutes to teach a lesson plan. State the null and alternative hypotheses. Fill in the correct symbol ( =, ≠, ≥, <, ≤, >) for the null and alternative hypotheses.

• \(H_{0}: \mu \_ 45\)
• \(H_{a}: \mu \_ 45\)
• \(H_{0}: \mu \geq 45\)
• \(H_{a}: \mu < 45\)

Example \(\PageIndex{4}\)

In an issue of U. S. News and World Report , an article on school standards stated that about half of all students in France, Germany, and Israel take advanced placement exams and a third pass. The same article stated that 6.6% of U.S. students take advanced placement exams and 4.4% pass. Test if the percentage of U.S. students who take advanced placement exams is more than 6.6%. State the null and alternative hypotheses.

• \(H_{0}: p \leq 0.066\)
• \(H_{a}: p > 0.066\)

Exercise \(\PageIndex{4}\)

On a state driver’s test, about 40% pass the test on the first try. We want to test if more than 40% pass on the first try. Fill in the correct symbol (\(=, \neq, \geq, <, \leq, >\)) for the null and alternative hypotheses.

• \(H_{0}: p \_ 0.40\)
• \(H_{a}: p \_ 0.40\)
• \(H_{0}: p = 0.40\)
• \(H_{a}: p > 0.40\)

COLLABORATIVE EXERCISE

Bring to class a newspaper, some news magazines, and some Internet articles . In groups, find articles from which your group can write null and alternative hypotheses. Discuss your hypotheses with the rest of the class.

In a hypothesis test , sample data is evaluated in order to arrive at a decision about some type of claim. If certain conditions about the sample are satisfied, then the claim can be evaluated for a population. In a hypothesis test, we:

• Evaluate the null hypothesis , typically denoted with \(H_{0}\). The null is not rejected unless the hypothesis test shows otherwise. The null statement must always contain some form of equality \((=, \leq \text{or} \geq)\)
• Always write the alternative hypothesis , typically denoted with \(H_{a}\) or \(H_{1}\), using less than, greater than, or not equals symbols, i.e., \((\neq, >, \text{or} <)\).
• If we reject the null hypothesis, then we can assume there is enough evidence to support the alternative hypothesis.
• Never state that a claim is proven true or false. Keep in mind the underlying fact that hypothesis testing is based on probability laws; therefore, we can talk only in terms of non-absolute certainties.

Formula Review

\(H_{0}\) and \(H_{a}\) are contradictory.

• If \(\alpha \leq p\)-value, then do not reject \(H_{0}\).
• If\(\alpha > p\)-value, then reject \(H_{0}\).

\(\alpha\) is preconceived. Its value is set before the hypothesis test starts. The \(p\)-value is calculated from the data.References

Data from the National Institute of Mental Health. Available online at http://www.nimh.nih.gov/publicat/depression.cfm .

Statistics Resources

• Excel - Tutorials
• Basic Probability Rules
• Single Event Probability
• Complement Rule
• Intersections & Unions
• Compound Events
• Levels of Measurement
• Independent and Dependent Variables
• Entering Data
• Central Tendency
• Data and Tests
• Displaying Data
• Discussing Statistics In-text
• SEM and Confidence Intervals
• Two-Way Frequency Tables
• Empirical Rule
• Finding Probability
• Accessing SPSS
• Chart and Graphs
• Frequency Table and Distribution
• Descriptive Statistics
• Converting Raw Scores to Z-Scores
• Converting Z-scores to t-scores
• Split File/Split Output
• Sampling Methods
• Partial Eta Squared
• Downloading and Installing G*Power: Windows/PC
• Correlation
• Testing Parametric Assumptions
• One-Way ANOVA
• Two-Way ANOVA
• Repeated Measures ANOVA
• Goodness-of-Fit
• Test of Association
• Pearson's r
• Point Biserial
• Mediation and Moderation
• Simple Linear Regression
• Multiple Linear Regression
• Binomial Logistic Regression
• Multinomial Logistic Regression
• Independent Samples T-test
• Dependent Samples T-test
• Testing Assumptions
• T-tests using SPSS
• T-Test Practice
• Quantitative Research Questions
• Null & Alternative Hypotheses
• One-Tail vs. Two-Tail
• Alpha & Beta
• Associated Probability
• Decision Rule
• Statement of Conclusion
• Statistics Group Sessions

ASC Chat Hours

ASC Chat is usually available at the following times ( Pacific Time):

If there is not a coach on duty, submit your question via one of the below methods:

  928-440-1325

  Ask a Coach

  [email protected]

Search our FAQs on the Academic Success Center's  Ask a Coach   page.

Once you have developed a clear and focused research question or set of research questions, you’ll be ready to conduct further research, a literature review, on the topic to help you make an educated guess about the answer to your question(s). This educated guess is called a hypothesis.

In research, there are two types of hypotheses: null and alternative. They work as a complementary pair, each stating that the other is wrong.

• Null Hypothesis (H 0 ) – This can be thought of as the implied hypothesis. “Null” meaning “nothing.”  This hypothesis states that there is no difference between groups or no relationship between variables. The null hypothesis is a presumption of status quo or no change.
• Alternative Hypothesis (H a ) – This is also known as the claim. This hypothesis should state what you expect the data to show, based on your research on the topic. This is your answer to your research question.

Null Hypothesis:   H 0 : There is no difference in the salary of factory workers based on gender. Alternative Hypothesis :  H a : Male factory workers have a higher salary than female factory workers.

Null Hypothesis :  H 0 : There is no relationship between height and shoe size. Alternative Hypothesis :  H a : There is a positive relationship between height and shoe size.

Null Hypothesis :  H 0 : Experience on the job has no impact on the quality of a brick mason’s work. Alternative Hypothesis :  H a : The quality of a brick mason’s work is influenced by on-the-job experience.

Was this resource helpful?

• << Previous: Hypothesis Testing
• Next: One-Tail vs. Two-Tail >>
• Last Updated: Dec 19, 2024 8:10 AM
• URL: https://resources.nu.edu/statsresources

Hypothesis Testing: Null Hypothesis and Alternative Hypothesis

Join over 2 million students who advanced their careers with 365 Data Science. Learn from instructors who have worked at Meta, Spotify, Google, IKEA, Netflix, and Coca-Cola and master Python, SQL, Excel, machine learning, data analysis, AI fundamentals, and more.

Figuring out exactly what the null hypothesis and the alternative hypotheses are is not a walk in the park. Hypothesis testing is based on the knowledge that you can acquire by going over what we have previously covered about statistics in our blog.

So, if you don’t want to have a hard time keeping up, make sure you have read all the tutorials about confidence intervals , distributions , z-tables and t-tables .

We've also made a video on null hypothesis vs alternative hypothesis - you can watch it below or just scroll down if you prefer reading.

Confidence intervals provide us with an estimation of where the parameters are located. You can obtain them with our confidence interval calculator and learn more about them in the related article.

However, when we are making a decision, we need a yes or no answer. The correct approach, in this case, is to use a test .

Here we will start learning about one of the fundamental tasks in statistics - hypothesis testing !

The Hypothesis Testing Process

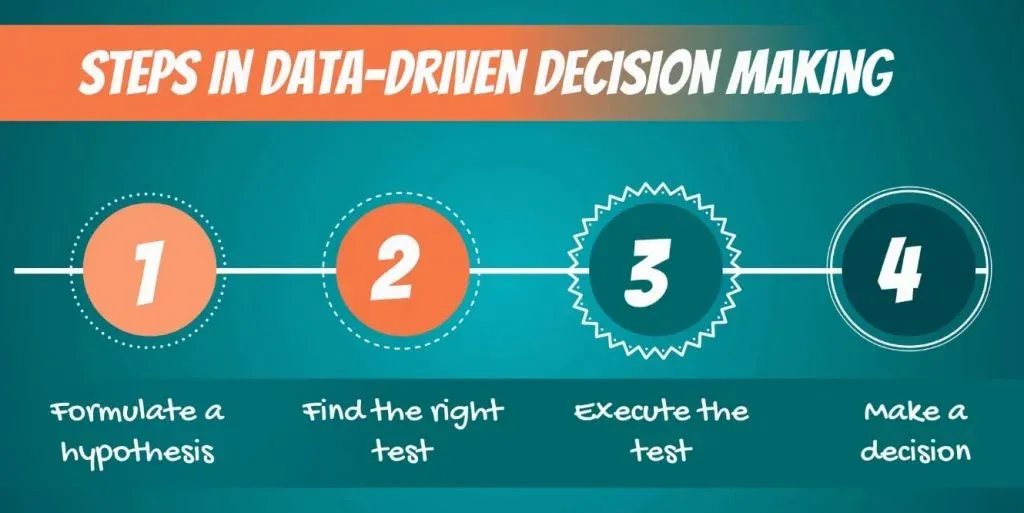
  First off, let’s talk about data-driven decision-making. It consists of the following steps:

• First, we must formulate a hypothesis .
• After doing that, we have to find the right test for our hypothesis .
• Then, we execute the test.
• Finally, we make a decision based on the result.

Let’s start from the beginning.

What is a Hypothesis?

Though there are many ways to define it, the most intuitive must be:

“A hypothesis is an idea that can be tested.”

This is not the formal definition, but it explains the point very well.

So, if we say that apples in New York are expensive, this is an idea or a statement. However, it is not testable, until we have something to compare it with.

For instance, if we define expensive as: any price higher than $1.75 dollars per pound, then it immediately becomes a hypothesis .

What Cannot Be a Hypothesis?

An example may be: would the USA do better or worse under a Clinton administration, compared to a Trump administration? Statistically speaking, this is an idea , but there is no data to test it. Therefore, it cannot be a hypothesis of a statistical test.

Actually, it is more likely to be a topic of another discipline.

Conversely, in statistics, we may compare different US presidencies that have already been completed. For example, the Obama administration and the Bush administration, as we have data on both.

A Two-Sided Test

Alright, let’s get out of politics and get into hypotheses . Here’s a simple topic that CAN be tested.

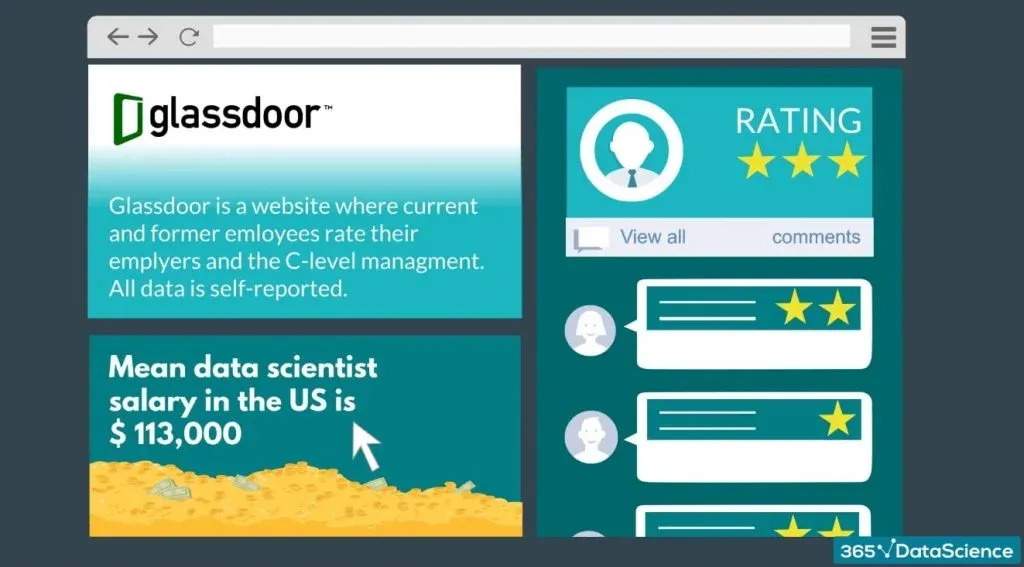
According to Glassdoor (the popular salary information website), the mean data scientist salary in the US is 113,000 dollars.

So, we want to test if their estimate is correct.

The Null and Alternative Hypotheses

There are two hypotheses that are made: the null hypothesis , denoted H 0 , and the alternative hypothesis , denoted H 1 or H A .

The null hypothesis is the one to be tested and the alternative is everything else. In our example:

The null hypothesis would be: The mean data scientist salary is 113,000 dollars.

While the alternative : The mean data scientist salary is not 113,000 dollars.

Author's note: If you're interested in a data scientist career, check out our articles Data Scientist Career Path , 5 Business Basics for Data Scientists , Data Science Interview Questions , and 15 Data Science Consulting Companies Hiring Now .

An Example of a One-Sided Test

You can also form one-sided or one-tailed tests.

Say your friend, Paul, told you that he thinks data scientists earn more than 125,000 dollars per year. You doubt him, so you design a test to see who’s right.

The null hypothesis of this test would be: The mean data scientist salary is more than 125,000 dollars.

The alternative will cover everything else, thus: The mean data scientist salary is less than or equal to 125,000 dollars.

Important: The outcomes of tests refer to the population parameter rather than the sample statistic! So, the result that we get is for the population.

Important: Another crucial consideration is that, generally, the researcher is trying to reject the null hypothesis . Think about the null hypothesis as the status quo and the alternative as the change or innovation that challenges that status quo. In our example, Paul was representing the status quo, which we were challenging.

Let’s go over it once more. In statistics, the null hypothesis is the statement we are trying to reject. Therefore, the null hypothesis is the present state of affairs, while the alternative is our personal opinion.

Why Hypothesis Testing Works

Right now, you may be feeling a little puzzled. This is normal because this whole concept is counter-intuitive at the beginning. However, there is an extremely easy way to continue your journey of exploring it. By diving into the linked tutorial, you will find out why hypothesis testing actually works.

Interested in learning more? You can take your skills from good to great with our statistics course!

Try statistics course for free

Next Tutorial:  Hypothesis Testing: Significance Level and Rejection Region

World-Class

Data Science

Learn with instructors from:

Iliya Valchanov

Co-founder of 365 Data Science

Iliya is a finance graduate with a strong quantitative background who chose the exciting path of a startup entrepreneur. He demonstrated a formidable affinity for numbers during his childhood, winning more than 90 national and international awards and competitions through the years. Iliya started teaching at university, helping other students learn statistics and econometrics. Inspired by his first happy students, he co-founded 365 Data Science to continue spreading knowledge. He authored several of the program’s online courses in mathematics, statistics, machine learning, and deep learning.

We Think you'll also like

Statistics Tutorials

False Positive vs. False Negative: Type I and Type II Errors in Statistical Hypothesis Testing

Hypothesis Testing with Z-Test: Significance Level and Rejection Region

Calculating and Using Covariance and Linear Correlation Coefficient

Visualizing Data with Bar, Pie and Pareto Charts