diagrammatic representation of data processing

Maths Notes Class 9
NCERT Solutions Class 9
RD Sharma Solutions Class 9
Maths Formulas Class 9
Class 9 Syllabus
Class 9 Revision Notes
Physics Notes Class 9
Chemistry Notes Class 9
Biology Notes Class 9
History Notes class 9
Geography Notes class 9
Social science Notes class 9

Graphical Representation of Data

Graphical Representation of Data: Graphical Representation of Data,” where numbers and facts become lively pictures and colorful diagrams . Instead of staring at boring lists of numbers, we use fun charts, cool graphs, and interesting visuals to understand information better. In this exciting concept of data visualization, we’ll learn about different kinds of graphs, charts, and pictures that help us see patterns and stories hidden in data.

There is an entire branch in mathematics dedicated to dealing with collecting, analyzing, interpreting, and presenting numerical data in visual form in such a way that it becomes easy to understand and the data becomes easy to compare as well, the branch is known as Statistics .

The branch is widely spread and has a plethora of real-life applications such as Business Analytics, demography, Astro statistics, and so on . In this article, we have provided everything about the graphical representation of data, including its types, rules, advantages, etc.

Table of Content

What is Graphical Representation

Types of graphical representations, line graphs, histograms , stem and leaf plot , box and whisker plot .

Graphical Representations used in Maths

Value-Based or Time Series Graphs

Frequency based, principles of graphical representations, advantages and disadvantages of using graphical system, general rules for graphical representation of data, frequency polygon, solved examples on graphical representation of data.

Graphics Representation is a way of representing any data in picturized form . It helps a reader to understand the large set of data very easily as it gives us various data patterns in visualized form.

There are two ways of representing data,

Pictorial Representation through graphs.

They say, “A picture is worth a thousand words”. It’s always better to represent data in a graphical format. Even in Practical Evidence and Surveys, scientists have found that the restoration and understanding of any information is better when it is available in the form of visuals as Human beings process data better in visual form than any other form.

Does it increase the ability 2 times or 3 times? The answer is it increases the Power of understanding 60,000 times for a normal Human being, the fact is amusing and true at the same time.

Check: Graph and its representations

Comparison between different items is best shown with graphs, it becomes easier to compare the crux of the data about different items. Let’s look at all the different types of graphical representations briefly:

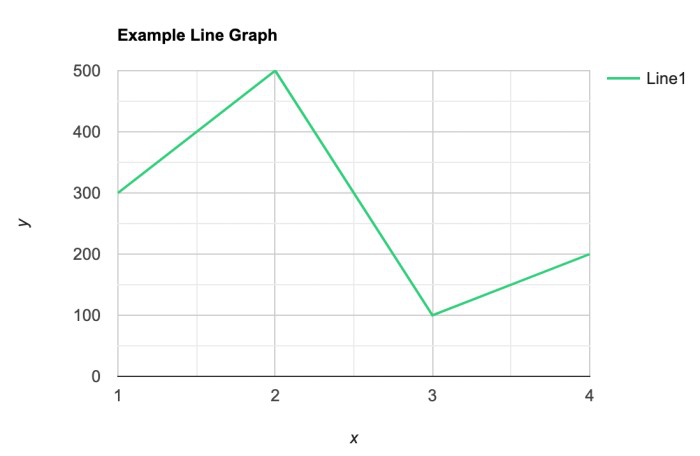
A line graph is used to show how the value of a particular variable changes with time. We plot this graph by connecting the points at different values of the variable. It can be useful for analyzing the trends in the data and predicting further trends.

diagrammatic representation of data processing

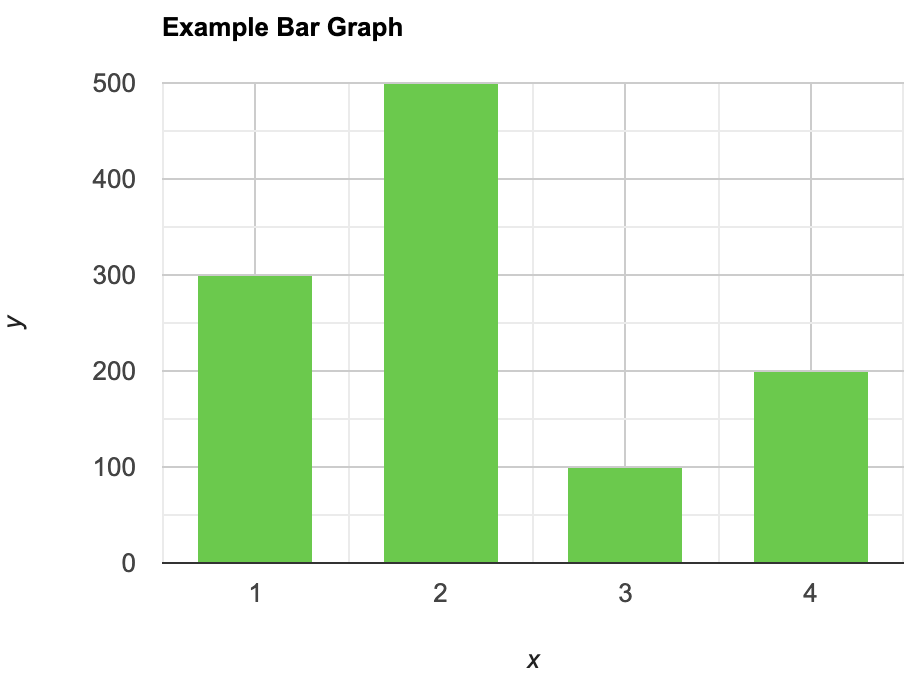
A bar graph is a type of graphical representation of the data in which bars of uniform width are drawn with equal spacing between them on one axis (x-axis usually), depicting the variable. The values of the variables are represented by the height of the bars.

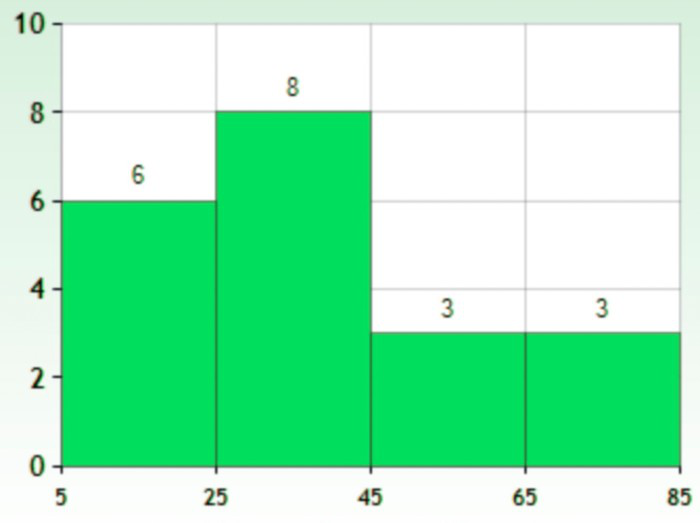
This is similar to bar graphs, but it is based frequency of numerical values rather than their actual values. The data is organized into intervals and the bars represent the frequency of the values in that range. That is, it counts how many values of the data lie in a particular range.

It is a plot that displays data as points and checkmarks above a number line, showing the frequency of the point.

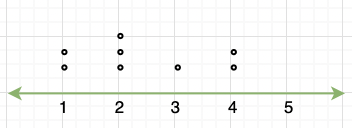
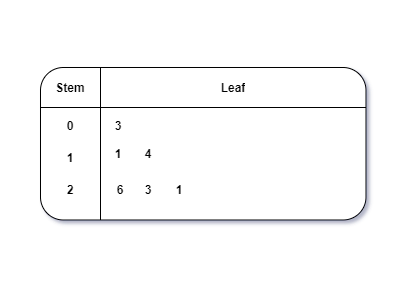
This is a type of plot in which each value is split into a “leaf”(in most cases, it is the last digit) and “stem”(the other remaining digits). For example: the number 42 is split into leaf (2) and stem (4).

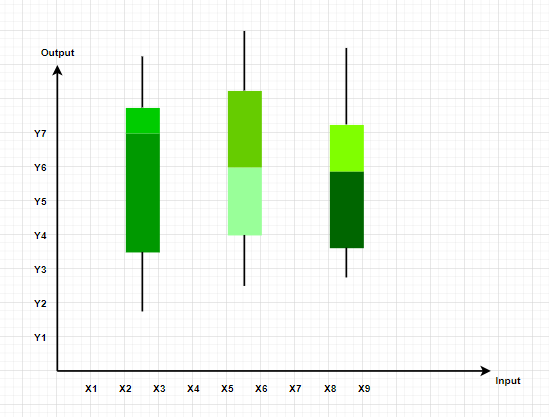
These plots divide the data into four parts to show their summary. They are more concerned about the spread, average, and median of the data.

It is a type of graph which represents the data in form of a circular graph. The circle is divided such that each portion represents a proportion of the whole.

Graphical Representations used in Math’s

Graphs in Math are used to study the relationships between two or more variables that are changing. Statistical data can be summarized in a better way using graphs. There are basically two lines of thoughts of making graphs in maths:

Value-Based or Time Series Graphs

These graphs allow us to study the change of a variable with respect to another variable within a given interval of time. The variables can be anything. Time Series graphs study the change of variable with time. They study the trends, periodic behavior, and patterns in the series. We are more concerned with the values of the variables here rather than the frequency of those values.

Example: Line Graph

These kinds of graphs are more concerned with the distribution of data. How many values lie between a particular range of the variables, and which range has the maximum frequency of the values. They are used to judge a spread and average and sometimes median of a variable under study.

Also read: Types of Statistical Data

All types of graphical representations follow algebraic principles.
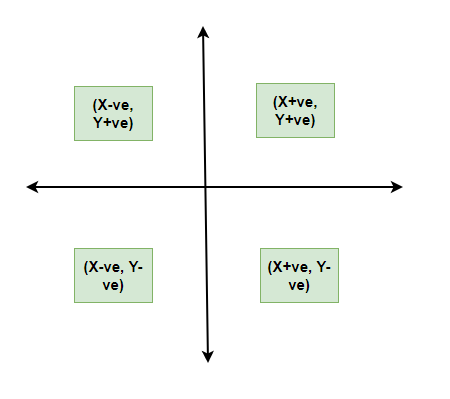
When plotting a graph, there’s an origin and two axes.
The x-axis is horizontal, and the y-axis is vertical.
The axes divide the plane into four quadrants.
The origin is where the axes intersect.
Positive x-values are to the right of the origin; negative x-values are to the left.
Positive y-values are above the x-axis; negative y-values are below.

It gives us a summary of the data which is easier to look at and analyze.
It saves time.
We can compare and study more than one variable at a time.

Disadvantages

It usually takes only one aspect of the data and ignores the other. For example, A bar graph does not represent the mean, median, and other statistics of the data.
Interpretation of graphs can vary based on individual perspectives, leading to subjective conclusions.
Poorly constructed or misleading visuals can distort data interpretation and lead to incorrect conclusions.

Check : Diagrammatic and Graphic Presentation of Data

We should keep in mind some things while plotting and designing these graphs. The goal should be a better and clear picture of the data. Following things should be kept in mind while plotting the above graphs:

Whenever possible, the data source must be mentioned for the viewer.
Always choose the proper colors and font sizes. They should be chosen to keep in mind that the graphs should look neat.
The measurement Unit should be mentioned in the top right corner of the graph.
The proper scale should be chosen while making the graph, it should be chosen such that the graph looks accurate.
Last but not the least, a suitable title should be chosen.

A frequency polygon is a graph that is constructed by joining the midpoint of the intervals. The height of the interval or the bin represents the frequency of the values that lie in that interval.

Question 1: What are different types of frequency-based plots?

Types of frequency-based plots: Histogram Frequency Polygon Box Plots

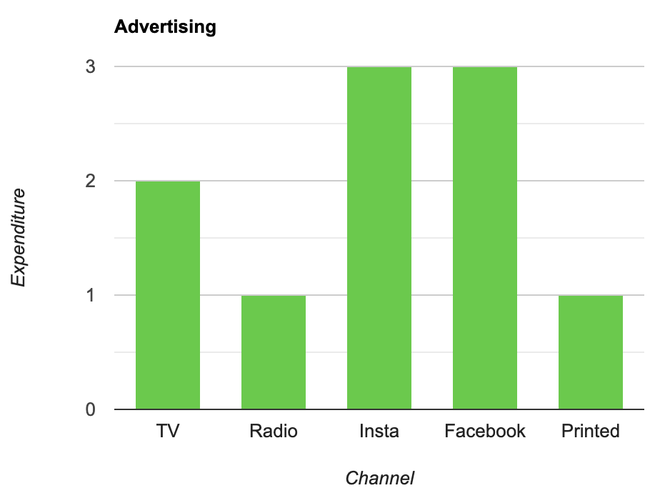
Question 2: A company with an advertising budget of Rs 10,00,00,000 has planned the following expenditure in the different advertising channels such as TV Advertisement, Radio, Facebook, Instagram, and Printed media. The table represents the money spent on different channels.

Draw a bar graph for the following data.

Put each of the channels on the x-axis
The height of the bars is decided by the value of each channel.

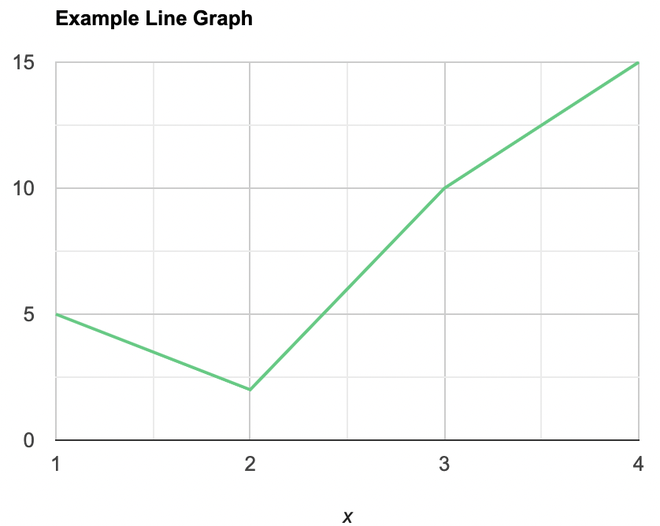
Question 3: Draw a line plot for the following data

Put each of the x-axis row value on the x-axis
joint the value corresponding to the each value of the x-axis.

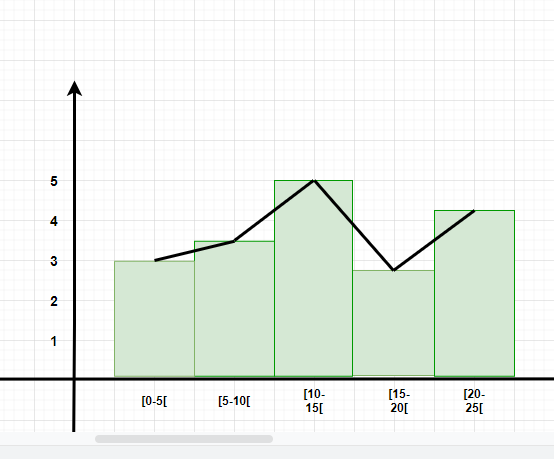
Question 4: Make a frequency plot of the following data:

Draw the class intervals on the x-axis and frequencies on the y-axis.
Calculate the midpoint of each class interval.

Now join the mid points of the intervals and their corresponding frequencies on the graph.

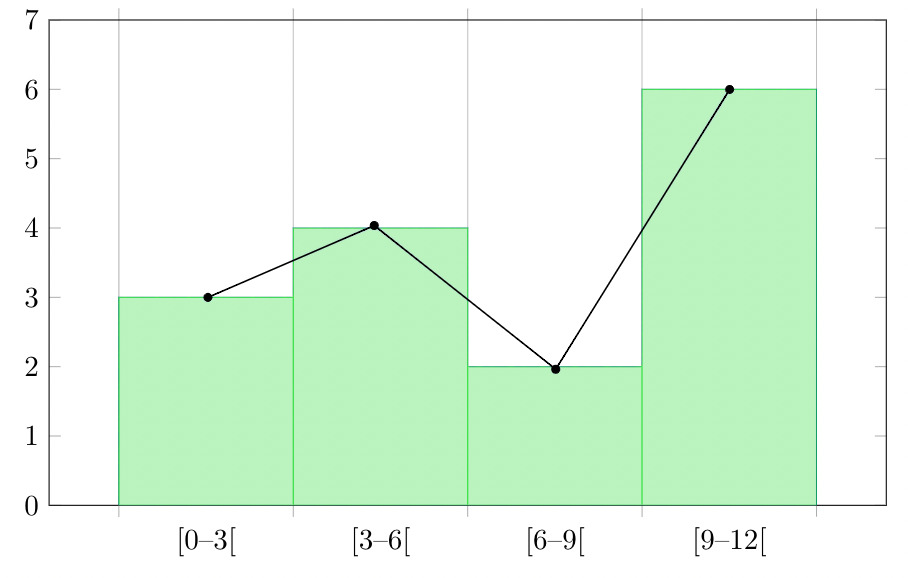
This graph shows both the histogram and frequency polygon for the given distribution.

Graphical Representation of Data| Practical Work in Geography Class 12 What are the different ways of Data Representation What are the different ways of Data Representation? Charts and Graphs for Data Visualization

Conclusion of Graphical Representation

Graphical representation is a powerful tool for understanding data, but it’s essential to be aware of its limitations. While graphs and charts can make information easier to grasp, they can also be subjective, complex, and potentially misleading . By using graphical representations wisely and critically, we can extract valuable insights from data, empowering us to make informed decisions with confidence.

Graphical Representation of Data – FAQs

What are the advantages of using graphs to represent data.

Graphs offer visualization, clarity, and easy comparison of data, aiding in outlier identification and predictive analysis.

What are the common types of graphs used for data representation?

Common graph types include bar, line, pie, histogram, and scatter plots , each suited for different data representations and analysis purposes.

How do you choose the most appropriate type of graph for your data?

Select a graph type based on data type, analysis objective, and audience familiarity to effectively convey information and insights.

How do you create effective labels and titles for graphs?

Use descriptive titles, clear axis labels with units, and legends to ensure the graph communicates information clearly and concisely.

How do you interpret graphs to extract meaningful insights from data?

Interpret graphs by examining trends, identifying outliers, comparing data across categories, and considering the broader context to draw meaningful insights and conclusions.

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Increase Font Size

4 Diagrammatic and Graphical Representation of Data I

Dr. Harmanpreet Singh Kapoor

Learning Objectives

Introduction.
Frequency Distribution
Use of Diagrammatic and Graphical Presentation of the Data
Suggested Readings

1. L earning Objectives

In this module, a complete explanation about different types of diagrammatic representation of data will be discussed. This module helps one to learn different methods of diagrammatic presentation and their properties. Through this module, one can learn about which method of representation is appropriate under what type of conditions. Questions with answers are included to give an in-depth knowledge of the topic.

2. Introduction

Statistics is a science that is based on description of data either numerically or diagrammatic or other way. This science is used to extract information from the data based on the objective. Data can be in quantitative form as well in qualitative form. Data are collected from the resources of study and are available in raw form. After collecting and editing the data the next stage is to organize the data. Classification and tabulation of the data are among the most important tools for the precise, clear and comprehensible representation of the data. However, sometimes these forms of presentation are not appealing to the common person. Due to technicality involved in these forms, it may not be interesting for a common person to be able to understand the things in a simple manner. Another way to represent the data is through diagram and graphs that present the data into attractive manner that appeal more to the mind of the spectators. These forms are more attractive, fascinating and impressive than the other methods. The best part of diagrammatic representation method is that even a layman person can understand this without any previous knowledge of statistics. This is the reason that diagrams and graphs are used to give basic education to the kids.

Another important feature of the diagrammatic and graphical representation is that it saves lot of time as these are easy to build up and one can draw meaningful inference from them. These methods are able to present that information that might be lost amid the details of classification and tabulation of data. These methods also facilitate the person for comparing the value of two or more sets of data. Graphs and charts are used to clarify a complex problem and reveal the hidden facts that are not clear from the tabular form. Hence, graphs and diagrams are important not only for the representation of the data but for visual comparison of two or more datasets. Now in the next section, a brief introduction about frequency distribution and how to form it will be discussed.

3. Frequency Distribution

In English language, frequency means the rate of occurrence of something in a repetitive manner in a particular time interval or time frame. Statistics is concerned with the extraction of information from the numbers collected in a raw form from the study. We already discussed about definition of variables in the second module.

In practical life, variables are used to represent these numbers in case of quantitative data like in a study of sales of luxury cars in a particular region in a year. One can consider “the sale of a car in a day” as a variable and note down the sale of a car in a day by variable where i=1,2,…..365. Here the values, 1, 2, … . . 365 represent the sales of a car in the first day of a year or financial year and similarly second day of the year and so on. The values of 1, 2, … . , 365 are known as the values of the variable.

Frequency of a value of the variable means the number of times a same value is repeated in the whole dataset. For example, if we assume that the no. of sales of a car are 2 units on 10th day, 3 units on 20th day, 2 units on the 45th day, 4 units on the 70th day of the year and so on. Here, 2 units appear two times, 3 and 4 units appear single time from the available information. So, from the available information the frequency of sale of 2 cars per day is two and other has only one. With an increase in the available information, one can construct frequency table that represent the repetition of the values in a dataset.

For example, let us consider the observation of sales of car in the month of February (28 values). These are 2, 3, 1, 2, 4, 5, 3, 2, 1, 3, 5, 6, 1, 2, 4, 2, 3, 5, 1, 3, 4, 2, 3, 5, 4, 1, 4, 2

Table No. 1

In the above table, we observe that for seven days two units of cars are sold, for six days three cars are sold and so on. Hence one can form the frequency table by counting the same observations in the data set this means frequency of a value of a variable is the number of times it occurs in a given series of observations. The table that represents the frequency of the value side by side is called frequency table . There are two forms of frequency distributions- Ungrouped frequency distribution and Grouped frequency distribution.

To understand the difference between two methods, we consider a data set of IQ score of 30 students and construct ungrouped and grouped frequency distribution.

Table No. 2

3.1 Ungrouped Frequency Distribution

Ungrouped frequency distribution table shows the frequency of the values in the dataset on individual basis. Table no. 3 is an example of ungrouped frequency distribution as the first column in the table represents the observations and second column shows corresponding frequency.

From Table No. 3, one can observe that 2nd column and 4th column show the frequency values of the dataset (from Table No. 2). Hence in ungrouped frequency distribution, the values of the dataset are shown on individual basis.

3.2 Group Frequency Distribution

In this method, the values of the variables are shown in the group or interval. In the following table, observations from Table no. 2 are used to present them in group frequency distribution. The smallest observation in the dataset is 35 and maximum value is 94. In Table no. 4, we consider width of the interval as 10 and lowest class value as 30 and so on till we cover the maximum value in the dataset. In the next section, we will discuss about how to choose, type of class, class interval, width of class interval etc.

From Table No. 4, we can see 70-80, 80-90 intervals have maximum frequency value that is 8. Hence we can conclude that IQ score of the most of the students lie between70 to 90.

On the comparison of Table No. 3 and Table No. 4, one can see that group frequency distribution visualize the important characteristics of the data in a simple and understandable manner about the tendency of IQ score of students over ungrouped frequency distribution.

Steps for forming a group frequency distribution

Many techniques are used for the formation of the group frequency distribution. For group of observations, we divide the data into class intervals and difference between upper and lower interval is called the width of the class interval. There are few points that must be kept in mind while preparing a group frequency table.

(a) C lass type : One should define class type in a very clear manner. It should be exhaustive and mutualy exclusive so that variable’s value must be assigned to only one class in the table.

(b) Class Intervals: It means how many intervals should be formed for the available data. Number of intervals depend on the things like number of observations in the data, its magnitude value, level of precision and further analysis of the data.

The most common formula that is used for the determination of the interval in the group frequency distribution is Sturge’s rule:

k= 1 + 3.322 log 10 N

where is the number of classes and N is the total number of observations in the data. This rule is used for correct determination of intervals in the data and it is further used for the determination of the width of the class interval.

(c) Width of class interval: Width of the interval means the difference between the lower limit and upper limit of the interval. The width of the interval is defined through the formula that is ℎ = Range/No. of Classes

where ℎ denote the width of the class interval and range is defined as the difference between the highest and lowest value of the data set.

(d) Class limits methods: There are different methods that are used for the classification of the data set on the basis of class interval. The limit consists of two numbers that are used for the purpose of tallying observations into various classes. There are two different methods for the classification of the data on the basis of class intervals. These are:- (a) Inclusive method and (b) Exclusive Method.

(i) Inclusive method: In inclusive method, the upper limit of a class interval is considered in the interval itself and is not related with the next class. For example, in inclusive method, the class limits are 0-4, 5-9, 10-14, 15-19 and so on. Hence one can see that both the upper and lower limits are included in the class and thus it is termed as inclusive. The main drawback of this method for continuous data observations for example if data value is 4.5 then with this method one cannot tabulate or assign the value to any interval.

(ii) Exclusive method: In this method, the data are classified into class interval of such time that upper limit of one interval is the lower limit of next succeeding class interval. For example, in exclusive method the class limits should be of such type that is 0-5, 5-10,10-15 and so on. Hence all those values that are less than 5 are considered in first interval and all those data values that are above than 5 but less than 10 are counted in second interval. Hence in exclusive method, the problem of inclusive method is taken care of.

(e) Mid value or Mid points: Mid value is calculated by taking the sum of upper and lower limit of the interval and dividing that sum by 2. This value is used as a representative value of the class interval and it is used for evaluation of mean, median, mode and higher moments of the data.

In the next section, we will discuss about cumulative frequency distribution and how to construct it.

3.3 Cumulative Frequency Distribution

We have already discussed about the frequency distribution in the previous section. Frequency distribution counts the occurrence of the same value in the data but sometime one is interested in the number of observations that are small or greater than a given value. In such type of situation, one has to calculate the accumulated frequency less than or greater than some specified value. This accumulated value is known as Cumulative frequency distribution.

The frequency of observations till a given value is considered as less than cumulative frequency and the frequency of observations that are greater than a value is called more than cumulative frequency.

Using the same observation as given in Table No.4. The cumulative frequency distribution for both more and less than are given in the following table.

Table No. 5

From the above table, one can see the less than and more than cumulative frequency values of the data. These values are further used for graphical representation of the data. For example, ogive curve of more than and less than type use these values for plotting on the axis.

4. Use of Diagrammatic and Graphical Presentation of the Data

Diagrammatic and Graphical presentation of the data are useful in practice due to the following reasons.

(1) The information that we acquire from the graphical and diagrammatic representation of the data is easy to understand even for a layman person due to its simplicity.

(2) People are more interested in graphical presentation of facts then just numbers due to eye caching effect of diagram or pictures.

(3) Graphs and picture can simplify the complexity of the data that cannot be easily be understood with the figures.

(4) With the graphical presentation, one can easily compare the statistical data relating to different time and places to bring out the hidden facts and relationship among the statistical variables.

There are some limitations of diagrammatic and graphical representations like they do not show the details behind the numbers that can only be shown from the table in a better way. A single diagram or graph does not have a great importance rather than it is used for comparison purpose with other diagram or graph. In the next section, difference between graph and diagram will be discussed so that reader can understand the difference between them in a clear manner and use them at their proper place without any confusion.

4.1 Difference between diagrams and graphs

There are few rules based on them, one can differentiate between graphs and diagram but these rules are not standard for all so there is scope of changes in these rules among different persons. But we will discuss few rules that are considered common for all. These rules are:

(a) Diagram are plotted on the paper while graphs are plotted on a paper called graph paper graphs helps in the study of mathematical or numerical relationship between variables but in diagram precise relationship among variables are not discussed.

(b) In diagram , different tools like bars, rectangles, circles etc are used to present the information in the data. Whereas in graphs, different tools like lines, dots etc are used to present the data.

(c) Diagrams only give approximate information regarding the data as this information will not be used further for analysis purpose. On the other hand, graphs give more precise, accurate information about the data and they are used for further analysis purpose.

(d) Diagrams are used for the presentation of the categorical and geographical information in the data. On the other hand, graphs are used for the presentation of the time series and frequency distribution.

(e) Diagrams are more eye catching than graphs. Also diagrams are used for the understanding of the layman person but graphs are used by experts from the field for the further analysis of the information.

(f) Graphs are easier to build than comparative to the diagram.

There are few points based on which one keep in mind while constructing the diagrams. These are:-

Diagram gives only a pictorial representation of the quantitative data for rough guesses;
it can only be used for homogenous data;
it is not reliable to make further inference about the data.

So, basically diagram are used for the graphical interpretation purpose only. One cannot use it to find out reasons or inference from the data.

While constructing diagrams, there are some general rules that should be followed. These are:-

An appropriate diagram can only present the data in a better way. Thus, it is essential to choose the right diagram for the data that need expertise as well as knowledge. It may be possible that due to inappropriate selection of diagram the interpretation might be wrong that can lead to unbearable results.
It is also important that a diagram should have an appropriate title corresponding to the nature of the data. With an appropriate title, a person can understand the main idea in the diagram.
It should be constructed in such a way that it portray all the relevant information within an allotted space. So, it should be appropriate in terms of size and consistent in terms of dimensions.
It should be neat, clean with footnotes and proper indexing that will attract the interest of the common man.

In the previous section, we discuss the characteristics of the appropriate diagram. Now in the following section, a brief note on different types of the diagrams will help to understand it importance.

4.2 Types of Diagrams

There are many types of diagram based on it dimensionality. These are

(i) One dimensional diagrams

(ii) Two dimensional diagrams

(iii) Pie Chart

(iv) Three dimensional diagrams

Each type of diagram is used for specific type of data i.e. for complex data, one need more dimensions to see the impact of one factor on the other. Hence the choice of the type of the data depends on the nature of the data. One dimensional diagram is discussed here to give elementary knowledge. One can read other dimensions diagram also from the references.

One dimensional diagrams

These types of diagram use only one dimension i.e. only length of bars and lines are taken into account. So, these diagrams are known as one-dimensional diagrams. Bars may be vertical or horizontal. Vertical bars are mostly used to represent growth or decline rate of the variable under study while horizontal bars are used to represent the data of attributes. There are few points that should be kept in mind while using bars.

(a) Bars should be constructed within an allotted space and of uniform shape and size. (b) Scale should be chosen according to the magnitude of the observations. (c) Bars must have the same base line for a given data. (d) It is better to represent the value at the top of the bar for the convenience of the reader. (e) Bars should be arranged from the left to right in order of magnitude for consistency.

The following example help you to understand the point given above.

The following data give the approximate average yield of rice in kg. per acre in different state of a country during a 2000-2001.

From the above figure, one can observe that the above diagram satisfies all the conditions. Hence one can easily understand the characteristics or facts of the data through diagrams in an easy manner.

Self- Checked Exercise

Question What are the benefits of using diagrammatic and graphical representation of the data?

Ans With the help of diagrammatic and graphical representation of the data even a layman person can understand the facts related with it. Although these techniques are not helpful to explain hidden factors influencing the variables or data.

Question How diagrammatic and graphical representation help in understanding the information contained in the data?

Ans As we are aware of the fact that one can understand the diagram or graphs in a better way than just numbers. Hence, one can easily understand the information contained in the data by using graphical and diagrammatical representations.

Question How graphical representation is different from diagrammatic presentation?

Ans In diagrammatic mode of presentation, one can use the devices like bars, rectangle etc whereas in graphical methods, one can use points, lines of different kind etc to present the information.

Data are collected from the resources of study and they are available in raw form. Thus after collecting and editing the data the next stage is to organize the data. Classification and tabulation of the data are among the most important tools for the precise, clear and comprehensible representation of the data. Frequency distribution and its various forms are discussed in the module. Graphical and diagrammatically forms and differences between them are discussed. Various forms of diagram one-diagram, two dimensional etc. are also used to represent the data in an understandable manner.

6. Suggested Readings

Agresti, A. and B. Finlay, Statistical Methods for the Social Science, 3rd Edition, Prentice Hall, 1997.

Daniel, W. W. and C. L. Cross, C. L., Biostatistics: A Foundation for Analysis in the Health Sciences, 10th Edition, John Wiley & Sons, 2013.

Hogg, R. V., J. Mckean and A. Craig, Introduction to Mathematical Statistics, Macmillan Pub. Co. Inc., 1978.

Meyer, P. L., Introductory Probability and Statistical Applications, Oxford & IBH Pub, 1975.

Triola, M. F., Elementary Statistics, 13th Edition, Pearson, 2017.

Weiss, N. A., Introductory Statistics, 10th Edition, Pearson, 2017.

One can refer to the following links for further understanding of the statistics terms.

http://biostat.mc.vanderbilt.edu/wiki/pub/Main/ClinStat/glossary.pdf

http://www.stats.gla.ac.uk/steps/glossary/alphabet.html

http://www.reading.ac.uk/ssc/resources/Docs/Statistical_Glossary.pdf

https://stats.oecd.org/glossary/

http://www.statsoft.com/Textbook/Statistics-Glossary

https://www.stat.berkeley.edu/~stark/SticiGui/Text/gloss.htm

https://stats.oecd.org/glossary/alpha.asp?Let=A

Diagrammatic Representation of Data

Suppose you are interested to compare the marks of your mates in a test. How can you make the comparison interesting? It can be done by the diagrammatic representations of data. You can use a bar diagram, histograms, pie-charts etc for this. You will be able to answer questions like –

How will you find out the number of students in the various categories of marks in a certain test? What can you say about the marks obtained by the maximum students? Also, how can you compare the marks of your classmates in five other tests? Is it possible for you to remember the marks of each and every student in all subjects? No! Also, you don’t have the time to compare the marks of every student. Merely noting down the marks and doing comparisons is not interesting at all. Let us study them in detail.

Browse more Topics under Statistical Description Of Data

Introduction to Statistics
Textual and Tabular Representation of Data
Frequency Distribution
Frequency Polygon
Cumulative Frequency Graph or Ogive

Construction of a Bar Diagram

Draw two perpendicular lines intersecting each other at a point O. The vertical line is the y-axis and the horizontal is the x-axis.
Choose a suitable scale to determine the height of each bar.
On the horizontal line, draw the bars at equal distance with corresponding heights.
The space between the bars should be equal.

Properties of a Bar Diagram

Each bar or column in a bar graph is of equal width.
All bars have a common base.
The height of the bar corresponds to the value of the data.
The distance between each bar is the same.

Types of Bar Diagram

A bar graph can be either vertical or horizontal depending upon the choice of the axis as the base. The horizontal bar diagram is used for qualitative data. The vertical bar diagram is used for the quantitative data or time series data. Let us take an example of a bar graph showing the comparison of marks of a student in all subjects out of 100 marks for two tests.

With the bar graph, we can also compare the marks of students in each subject other than the marks of one student in every subject. Also, we can draw the bar graph for every student in all subjects.

We can use another way of diagrammatical representation of data. If we are working with a continuous data set or grouped dataset, we can use a histogram for the representation of data.

A histogram is similar to a bar graph except for the fact that there is no gap between the rectangular bars. The rectangular bars show the area proportional to the frequency of a variable and the width of the bars represents the class width or class interval.
Frequency means the number of times a variable is occurring or is present. It is an area graph. The heights of the rectangles are proportional to the corresponding frequencies of similar classes.

Construction of Histogram

Choose a suitable scale for both the axes to determine the height and width of each bar
On the horizontal line, draw the bars with corresponding heights
There should be no gap between two consecutive bars showing the continuity of the data
If the grouped frequencies are not continuous, the first thing to do is to make them continuous

It is done by adding the average of the difference between the lower limit of the class interval and the upper limit of the preceding class width to the upper limits of all the classes. The same quantity is subtracted from the lower limits of the classes.

Properties of Histogram

Each bar or column in a bar graph is of equal width and corresponds to the equal class interval
If the classes are of unequal width then the height of the bars will be proportional to the ration of the frequencies to the width of the classes
All bars have a common base
The height of the bar corresponds to the frequency of the data

Suppose we have a data set showing the marks obtained out of 100 by a group of 35 students in statistics. We can find the number of students in the various marks category with the help of the histogram.

A line graph is a type of chart or graph which shows information when a series of data is joined by a line. It shows the changes in the data over a period of time. In a simple line graph, we plot each pair of values of (x, y). Here, the x-axis denotes the various time point (t), and the y-axis denotes the observation based on the time.

Properties of a Line Graph

It consists of Vertical and Horizontal scales. These scales may or may not be uniform.
Data point corresponds to the change over a period of time.
The line joining these data points shows the trend of change.

Below is the line graph showing the number of buses passing through a particular street over a period of time:

Solved Examples for diagrammatic Representation of Data

Problem 1: Draw the histogram for the given data.

Solution: This grouped frequency distribution is not continuous. We need to convert it into a continuous distribution with exclusive type classes. This is done by averaging the difference of the lower limit of one class and the upper limit of the preceding class. Here, d = ½ (19 – 18) = ½ = 0.5. We add 0.5 to all the upper limits and we subtract 0.5 from all the lower limits.

The corresponding histogram is

Draw a line graph for the production of two types of crops for the given years.

Solution: The required graph is