mirror problem solving with solution

• Physics Class-12th Notes
• Physics Formulas
• Physics Symbol
• Application of Physics
• Class 8 Science
• Class 9 Science
• Class 10 Science
• Class 11 Science
• Class 12 Science
• Class 8 Study Material
• Class 9 Study Material
• Class 10 Study Material
• Class 11 Study Material
• Class 12 Study Material

Solve Problems on Mirror and Magnification Formula

Mirror and magnification formulas are fundamental equations used in optics to describe the formation of images by mirrors. These formulas are commonly applied in geometrical optics, which deals with the behavior of light rays using the principles of geometry. This article contains mirror and magnification formula and problems based on it in detail.

Mirror Formula

The mirror formula shows the relationship between the object distance, image distance, and the focal length of the spherical mirror. Hence, the formula is given as,

1/u + 1/v  = 1/f

where, 

• u is the object distance, 
• v is the image distance, and 
• f is the focal length of the mirror

While solving numerical problems using mirror formula one must remember two important things according to the sign convention for spherical mirrors, that are: If object is at left side of the mirror the object distance is taken as negative, if it is in right it is positive. For focal length the sign is depend on type of mirror we are using if mirror is concave then focal length is taken negative and if mirror is convex then focal length is positive .

Mirror formula in terms of Radius of Curvature:

Since, the radius of curvature (R) is two times its focal length (f), that is

R = 2f or  f = R/2

Hence, the Mirror Formula can be written as:

1/u + 1/v = 1/f = 2/R

Magnification

One must have noticed that there is simply an increase or decrease in the size of image by concave or convex mirror, this is a magnification of the object. 

• Magnification is defined as the ratio of the height of the image (h i ) to the height of the object (h o ).

Magnification = Height of image / Height of object

m = H i  / H o

Magnification can also be defined as the ratio of the image distance (v) and the object distance from the mirror (v).

Magnification = -Image distance / Object distance 

Determination of the Nature of the Image formed by a spherical mirror:

• The positive magnitude of magnification shows us that a virtual and erect image is formed.
• The negative  magnitude of magnification shows us that a real and inverted image is formed.

Also, Check

• Mirror Equation
• Image Formation by Spherical Mirror
• Lens Maker’s Formula

Problems on Mirror Formula and Magnification Formula

Problem 1: An object is placed at a distance of 2 times of focal length from the pole of the convex mirror, Calculate the linear magnification.

Let the Focal length of mirror = f So, the object distance, u = -2f  The formula to calculate image distance we use mirror formula as, 1 / v + 1 / u = 1 / f Therefore, 1 / v + 1 / -2f = 1 / f  1 / v  = 1 / f + 1 / 2f   1 / v = 3 / 2f or v = 2f / 3 Magnification is given as,  m = – v / u = -(2f/3) / (-2f)  =   1/3

Problem 2. If the image is a distance of 6 cm and the object is at 12 cm in the front of the concave mirror, Calculate the magnification formed.

Given that, The distance of object, u = – 12 cm The distance of image, v = – 6 cm Since, Magnification is given by,  m = – v / u Therefore, m = – (-6 / -12)  = -0.5 Hence, the image will be diminished by nearly half as size of object. 

Problem 3: In the experiment height of the image is 12 cm whereas the height of the object is 3 cm, would you determine the magnification formed.

Given that,  Height of image = 12 cm  Height of object = 3 cm Magnification in terms of height is given by, m = height of image / height of object = 12 / 3  = 4 Therefore magnification is 4 .

Problem 4: In the case of a concave mirror if the object is placed at the distance of 12 cm. Determine the image distance from the mirror if the height of the object to image ratio is 1:2.

Given that, The object distance, u = -12 cm Ratio of object to image height = 1/2 Magnification = height of image / height of object   = 1/ (1/2)  = 2 Now, magnification in terms of distance of object and image from the mirror, m = – v / u = – v / -12  2 = v / 12   or  v = 12 × 2  = 24 Therefore the distance of image from the mirror is equal to 24 cm .

Problem 5: Calculate the change in the size of the image formed, if the object distance is 18 cm and the distance of the image is 6 cm from the concave mirror. 

Given that, The object distance, u = -12 cm Image distance, v = – 6cm Magnification,  m = – v/u  = – (-6 / -18)  = -1/3 which means that size of image is 1/3 rd of the size of object.

Problem 6: The radius of curvature of the rear view convex mirror of the truck is 6 m. If the car is 8 m from the mirror of the truck. Calculate the distance at which the image is formed.

Given that, Radius of curvature, R = 6 m  Object distance, u = -8 m Focal length is half of Radius of curvature, f = R/2  =  6/2  = 3 m Using mirror formula  1 / v + 1 / u = 1 / f 1 / v + 1 / -8 = 1 / 3 1 / v  = 1 / 3 + 1 / 8 = 11 / 24 v = 24 / 11 m The image is formed at distance of 24 / 11 behind the mirror.

Problem 7: A concave mirror produces an image of size n times that of the object and of focal length f. If the image is real then find the distance of the object from the mirror.

Given that Size of image = n × size of object n = Size of image /  size of object  = magnification Since the image is real, it must be inverted hence magnification will be negative,  m = -n Let d is the distance of object then, m = -v/u   -n = -v / d  or v = nd Therefore, the mirror formula: 1 / f = 1/v + 1/u becomes, 1/f = 1/nd + 1/d or 1/f = 1/d(1/n + 1) or 1/d = n/ f(n + 1) Therefore, d = f (n + 1)/ n

Problem 8: Where should the object be placed to obtain a magnification of 1/3? If an object is placed at a distance of 60 cm from a convex mirror, then the magnification produced is 1/2. 

Given that, u = -60 cm m  = 1/2  So, -v/u = 1/2  and  v/60 = 1/2 or v = 30 cm Since, the mirror formula is: 1 / v + 1 / u = 1 / f Therefore, 1 / 30 + 1 / (-60) = 1/f 1/f = ( 2-1 ) / 60 = 1 / 60 f = 60 cm Now for magnification = 1 / 3, – v / u = 1 / 3 or  v = – u / 3  using mirror formula  1 / v + 1 / u = 1 / f 1 / (-u/3) + 1/ u = 1/ 60 -3/ u + 1/u = 1/60 -2/ u = 1/60 or  u = -120 cm object should be placed at 120 cm in front of mirror to get magnification of 1/3.

Problem 9: In the case of a concave mirror, if the object distance is 11 cm, its focal length is 11 cm then, Calculate the image distance.

Given that, Distance of object, u = -11 cm Focal length, f = -11cm Using mirror formula, 1 / v + 1 / u = 1 / f Therefore, 1 / v + 1 / -11 = 1/ -11 So, 1/v = 0 or  v = infinity This means that image will be at infinity if object is present at the focal length.

Problem 10: If the object distance is 32 cm in front of the concave mirror, the focal length of the mirror is 16 cm. State the nature and the size of the image formed.

Given that, Object distance, u = -32 cm Focal length , f = -16 cm For image distance use mirror formula, 1 / v + 1 / u = 1 / f Therefore, 1/ v + 1/ -32 = 1/ -16 or  1/ v = 1/ -16 + 1/ 32 or 1/ v = (-2 + 1) / 32 So, v = -32 cm Hence the image is located 16 cm in front of the mirror. and the image formed is real and inverted.  Size of image will be same as that of object, as it is located at center of curvature.

Similar Reads

• Solve Problems on Mirror and Magnification Formula Mirror and magnification formulas are fundamental equations used in optics to describe the formation of images by mirrors. These formulas are commonly applied in geometrical optics, which deals with the behavior of light rays using the principles of geometry. This article contains mirror and magnifi 8 min read
• Mirror Formula and Magnification The light gets reflected or refracted from the surfaces or medium. Any surface which is polished or in other words shiny always acts like a mirror be it of any kind. The observation of light bouncing off or getting back from the surfaces is termed as reflection. The light after the case of reflectio 9 min read
• Lens Formula and Magnification The light is an electromagnetic, transverse, wave that can be seen or caught by the typical human eye. The wave nature of light was first illustrated through the experiments on diffraction and interference. When these light rays fall onto the lenses then lenses behave depending on the type of lens i 12 min read
• What is Lens Formula and Magnification? Light is a kind of energy that can be seen with the naked eye. We observe objects and understand the world around us mostly via the use of light. Light travels in a straight path at an extremely fast speed of around 3 × 108 ms. A small light source produces a strong shadow on an opaque object. This 10 min read
• Height of a Parallelogram - Formula and Solved Examples Height of a Parallelogram formula is to calculate the height of a Parallelogram. The height of a Parallelogram is the perpendicular distance between the base side and the parallel side opposite to it. A Parallelogram can be defined as a quadrilateral in which opposite sides are parallel and the leng 4 min read
• Reflection and Ray Model of Light Formula Reflection of light is a very important concept in physics. After all, this phenomenon is what allows us to see the world around us. In this article, the reflection of light is discussed. Law of Reflection A ray of light(incident) falling on a polished surface is shown to bounce back after striking 3 min read
• Practice Problems on Heron's Formula with Solutions Heron's formula is also known as Hero's formula. It calculates the area of triangles or quadrilaterals based on the lengths of their sides. It does not consider the angles of the shapes, only their side lengths. The formula includes the semi-perimeter, which is symbolized by "s", which is half the p 5 min read
• Derivation of Mirror formula A spherical mirror or a mirror that is a part of a sphere is a mirror that has the shape of a piece that is cut out of a spherical surface or material. There are two types of spherical mirrors that are the concave and convex mirror. The curved surface we see of a shining or a shiny spoon can be cons 9 min read
• Image Formation by Spherical Mirror Image Formation by Spherical Mirror-You might have observed that the image formed in the side view mirror of a car is smaller while the image formed in the rear-view mirror is larger than the actual size of the objects. The dentist uses a small mirror to examine the teeth of a patient. You might hav 7 min read
• Image Formation in Convex Mirror Convex Mirror also called Diverging Mirror is a curved reflective surface that bulges outward. The image formed by a convex mirror is always erect, virtual, and diminished in size. The image formed by a convex mirror is generally formed behind the mirror. In this article, we will understand the mean 6 min read
• Real Life Applications of Concave Mirror Concave mirror is widely used as shaving mirror, in headlights of cars and bikes etc. Concave Mirror is a converging mirror and generally produces enlarged images. In this article, we will learn about the real-life applications of concave mirror. We will look how concave mirror is used in various as 3 min read
• Functions of Microscope A Microscope is an apparatus that enhances the views of tiny substances. It gives the viewer a remarkably close-up picture of minuscule structures at a scale suitable for scrutiny and study. Invisible to the human sight microscopic items are magnified using the microscope. Additionally, a microscope 8 min read
• Volume of a Triangular Prism Formula A prism is a three-dimensional solid figure with two identical ends. It is made up of flat sides, similar bases, and equal cross-sections. Its faces are parallelograms or rectangles without bases. Such a prism that has three rectangular faces and two parallel triangle bases is called a triangular pr 3 min read
• Write Five Uses of a Convex Mirror. Answer: Convex mirrors, with their outward-curving reflective surfaces, have several practical applications due to their unique property of diverging light rays. Here are five uses of a convex mirror: Vehicle Rear-View Mirrors: Convex mirrors are widely used in the side-view mirrors of vehicles. The 2 min read
• Concave and Convex Mirrors Mirrors are surfaces that reflect almost all types of incident light rays that hit their surface. The mirror can have either a plane or a curved surface. On this basis, mirrors are divided into two: Spherical Mirrors and Plane Mirrors. Plane mirrors simply mirror having plain and polished reflecting 15 min read
• Applications of Heron's Formula While solving and finding the Area of a Triangle, Certain parameters are expected to be provided beforehand, for example, the height and the base of the triangle must be available Or in the case of an Equilateral Triangle, the lengths of the side should be given. Heron's formula is basically for a t 10 min read
• Propagation Constant Formula Electromagnetic waves travel in a sinusoidal pattern. The propagation constant is defined as the change in amplitude and phase per unit distance. It can be measured as a field vector, such as electric flux density or electric field strength, or it can be measured as the current or voltage in the cir 4 min read
• Image formation by Spherical Lenses You might have used a microscope in the science lab for magnifying the micro-size object. It basically magnifies tiny objects and we can see the enlarged image of that object. Telescopes are used by scientists to the planets and stars which are far- far away from the earth. You might see the spectac 7 min read
• Image Formation by Lenses In optics, a ray is a geometrical representation of the light that is idealized by choosing a curve that is perpendicular to the wave fronts of actual light and points in the energy flow direction. Rays are used to represent the propagation of light through an optical system by separating the real l 9 min read
• Geeks Premier League
• School Learning
• School Physics
• Geeks-Premier-League-2022
• Physics-Class-12

Improve your Coding Skills with Practice

What kind of Experience do you want to share?

Gurumuda Networks

Concave mirror – problems and solutions

1. An object is placed 10 cm from a concave mirror . The focal length is 5 cm. Determine (a) The image distance (b) the magnification of image

The focal length (f) = 5 cm

The object distance ( d o ) = 10 cm

Formation of image by concave mirror :

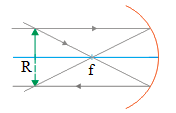
The image distance :

1/ d i = 1/f – 1/ d o = 1/5 – 1/10 = 2/10 – 1/10 = 1/10

d i = 10/1 = 10 cm

The image distance is 10 cm.

The magnification :

m = – d i / d o = -10/10 = -1

1 means that the image is the same as the object.

The minus sign indicates that the image is inverted. If the sign is positive than the image is upright.

2. A 5-cm-high object is placed in front of a concave mirror with a radius of curvature of 20 cm. Determine the image height if the object distance is 5 cm, 15 cm, 20 cm, 30 cm.

The radius of curvature ( r ) = 20 cm

The focal length (f) = R/2 = 20/2 = 10 cm

The object height (h o ) = 5 cm

a) the focal length (f) = 10 cm and the object distance ( d o ) = 5 cm

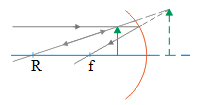
The image distance ( d i ) :

1/ d i = 1/f – 1/ d o = 1/10 – 1/5 = 1/10 – 2/10 = -1/10

d i = -10/1 = -10 cm

The minus sign indicates that the image is virtual or the image is behind the mirror.

The magnification of image ( m ) :

m = – d i / d o = -(-10)/5 = 10/5 = 2

The plus sign indicates that the image is upright.

The image height ( h i ) :

m = h i / h o

h i = h o m = (5 cm)(2) = 10 cm

The image height is 10 cm.

b) The focal length (f) = 10 cm and the object distance ( d o ) = 15 cm

1/ d i = 1/f – 1/ d o = 1/10 – 1/15 = 3/30 – 2/30 = 1/30

d i = 30/1 = 30 cm

The plus sign indicates that the image is real or the image is 30 cm in front of the mirror, on the same side as the object.

m = – d i / d o = -30/15 = -2

The minus sign indicates that the image is inverted.

The image is 2 times larger than the object.

The image height (h i ) :

c) The focal length (f) = 10 cm and the object distance ( d o ) = 20 cm

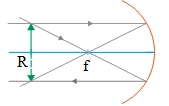
The image distance (d i ) :

1/ d i = 1/f – 1/ d o = 1/10 – 1/20 = 2/20 – 1/20 = 1/20

d i = 20/1 = 20 cm

The positive sign indicates that the image is real or the image is 20 cm in front of the mirror, on the same side as the object.

m = – d i / d o = -20/20 = -1

The negative sign means the image is inverted.

The image height ( hi ) :

h i = h m = (5 cm)(1) = 5 cm

d) The focal length (f) = 10 cm and the object distance ( d o ) = 30 cm

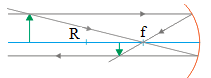
1/ d i = 1/f – 1/ d o = 1/10 – 1/30 = 3/30 – 1/30 = 2/30

d i = 30/2 = 15 cm

The plus sign indicates that the image is real or the image is 15 cm in front of the mirror, on the same side as the object.

The magnification of image ( m) :

m = – d i / d o = -15/30 = -0.5

The image is 0.5 smaller than the object.

h i = h o m = (5 cm)(0.5) = 2.5 cm

3. An image an by a concave mirror is 4 times greater than the object. If the radius of curvature 20 cm, determine the object distance in front of the mirror!

The magnification of image ( m ) = 4

The focal length (f) = r /2 = 20/2 = 10 cm

Wanted : The object distance ( d o )

m = – d i / d o

4 = – d i / d o

– d i = 4 d o

d i = – 4 d o

1/f = 1/ d o + 1/ d i

1/10 = 1/ d o + 1/4 d o

4/40 = 4/4 d o + 1/4 d o

4/40 = 5/4 d o

(4)(4s) = (5)(40)

16 d o = 200

d o = 12.5 cm

The object distance = 12.5 cm.

4 . A 1-cm high object is placed 10 cm from a concave mirror with the focal length, f = 15 cm. Determine :

A. The image distance ?

B. The image height?

C. The properties of image formed by the concave mirror?

The object height (h) = 1 cm

The object distance (d o ) = 10 cm

The focal length of the concave mirror (f) = 15 cm

A. The image distance (d i )

1/f = 1/d o + 1/d i

1/d i = 1/f – 1/d o = 1/15 – 1/10 = 2/30 – 3/30 = -1/30

d i = -30/1 = -30 cm

The negative sign indicates that the image is virtual or the image is behind the mirror.

B. The image height (h i )

The magnification of the image (M) :

M = -d i /d o = h i /h o

M = -(-30)/10 = 30/10 = 3 times

M = h i / h o

3 = h i / 1 cm

h i = 3 (1 cm)

the image height is 3 cm. The plus sign indicates that the image upward.

C. The properties of the image :

Virtual, upward, larger than object

5 . The magnification of the image, according to the image below.

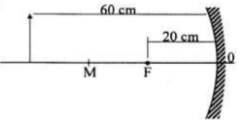
The object distance (d o ) = 60 cm

The focal length (f) = 20 cm

Wanted : The image magnification (M)

1/d i = 1/f – 1/d o = 1/20 cm – 1/60 cm = 3/60 cm – 1/60 cm = 2/60 cm

d i = 60/2 cm = 30 cm

M = d i /d o = 30 cm / 60 cm = 1/2 times

6 . If the object is placed 6 cm from a concave mirror, the image distance is 12 cm as shown in figure below. Whhat is the image distance if the object is moved from the original position 1 cm away from the mirror.

The object distance (d o ) = 6 cm

The image distance (d i ) = 12 cm

Wanted : if the object distance (d o ) = 7 cm then the image distance is …

1/f = 1/do + 1/di = 1/6 + 1/12 = 2/12 + 1/12 = 3/12

f = 12/3 = 4 cm

The focal length is positive, means that the focal point is real or the rays pass through the point.

1/d i = 1/f – 1/d o = 1/4 – 1/7 = 7/28 – 4/28 = 3/28

d i = 28/3 = 9.3 cm

7. A dentist observes and checks the patient’s teeth using a mirror with an 8 cm radius. In order for the hole to be seen clearly by the doctor, what is the distance between the patient’s teeth and the mirror?

A. less than 4 cm in front of a concave mirror

B. less than 4 cm in front of a convex mirror

C. more than 4 cm in front of the concave mirror

D. more than 4 cm in front of the convex mirror

Radius of mirror (r) = 8 cm

The focal length of mirror (f) = r / 2 = 8 / 2 = 4 cm

Wanted : The distance between the patient’s teeth and the mirror

The mirror used is a concave mirror or a convex mirror? In order for the tooth hole to be clearly visible by the doctor, the mirror used should be able to enlarge the image of the tooth and the image must be upright. Convex mirror always produces inverted images and the size of the image is smaller than the size of the object. Conversely a concave mirror can produce an upright image if the object distance (d) is smaller than the focal length (f). If the object distance is greater than the focal length (f) then the concave mirror produces an inverted image.

The focal length (f) of the concave mirror is 4 cm, therefore the patient’s teeth should be less than 4 cm in front of a concave mirror.

The correct answer is A.

8. A concave mirror has a radius of curvature of 24 cm. If the object is placed 20 cm in front of the mirror then determine the properties of the image.

A. Real, upright and enlarged

B. Real, inverted and enlarged

C. Virtual, upright and enlarged

D. Virtual, inverted and smaller

Radius of curvature (r) = 24 cm

Focal length (f) = R/2 = 24/2 = +12 cm

The focal length of the concave mirror is positive or real because the light passes through the focal point of the mirror.

Object distance (d) = 20 cm

Wanted : Properties of image

Image is virtual or real? Calculate the image distance (s’):

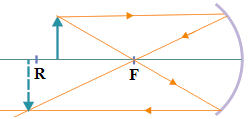
1/d’ = 1/f – 1/d

1/d’ = 1/12 – 1/20

1/d’ = 5/60 – 3/60

1/d’ = 2/60

The image distance signed positive means that the image is real because it is passed by light.

Image enlarged ? Upright or inverted? First calculate the image magnification (M):

M = -d’ / d = -30/20 = -1.5

M > 1 means the image is enlarged, M has a negative sign means an inverted image. So the image properties are real, inverted, enlarged.

The correct answer is B.

9. A spherical mirror produces an image has size 5 times greater than the object on a screen, 5 meters away from the object. The mirror is…..

A. concave with the focal length of 25/24 m

B. convex with the focal length of 25/24 m

C. concave with the focal length of 24/25 m

D. convex with the focal length of 24/25 m

Magnification of image (M) = 5 times

The distance between object and image = 5 meters

The size of the image produced by a convex mirror is always smaller than the size of the object, therefore, the mirror is a concave mirror.

Object distance (d) = x

Image distance (d’) = x + 5

Image magnification (M) = 5 times

The formula of image magnification :

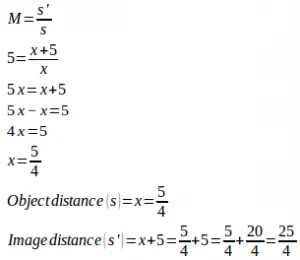
The formula of the focal length (f) :

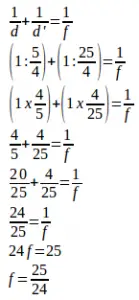
[wpdm_package id=’858′]

• Concave mirror problems and solutions
• Convex mirror problems and solutions
• Diverging lens problems and solutions
• Converging lens problems and solutions
• Optical instrument human eye problems and solutions
• Optical instrument contact lenses problems and solutions
• Optical instrument eyeglasses
• Optical instrument magnifying glass problems and solutions
• Optical instrument microscope – problems and solutions
• Optical instrument telescopes problems and solutions

Share this:

Leave a comment cancel reply.

• Exam Center
• Ticket Center
• Flash Cards

Concave Mirror: Problems with Answers for AP Physics 2

Here, using the mirror equation and magnification formula for curved mirrors a number of problems on the concave mirror are solved which is helpful for the AP Physics 2 exam.

We tried to illustrate all properties of the image formed by a concave mirror using equations and ray diagrams for a deeper understanding. 

Summary of concave spherical mirrors

Mirror equation is \[\frac{1}{f}=\frac{1}{d_i}+\frac{1}{d_o}\] Where $f, d_i, d_o$ are the focal length, image distance and the object distance, respectively. 

The magnification formula for spherical mirrors is also written as \[M=-\frac{d_i}{d_o}=\frac{h_i}{h_o}\] where $h_i, h_o$ are the image and object heights, respectively. 

Sign Rules for Concave mirror:

• The focal length is positive $f>0$. 
• The image distance must be inserted positive $d_i>0$ if the image is formed in front of the mirror.
• The image distance must be inserted negative $d_i<0$ if the image is formed back of the mirror.

Note : In front of the mirror is where the object is placed. 

Concave Mirror Solved Problems:

Problem (1): A pencil is placed 6 cm in front of a concave mirror having a radius of curvature of 40 cm.  (a) What is its focal length? (b) Determine the position of the image formed by this mirror.  (c) Draw a ray diagram and verify your previous results. (d) What do we conclude from this problem?

Solution: (a) Recall that the focal length $f$ of a spherical mirror is related to the radius of curvature $R$ by the following formula \[f=\frac R2\] Substituting the known value into the above, we get \[f=\frac R2=\frac {40}{2}=20\quad {\rm cm}\]  (b) Using the mirror equation below and solving for unknowns such as image distance $d_i$ or object distance $d_o$, we complete our calculation. \[\frac{1}{d_i}+\frac{1}{d_o}=\frac{1}{f}\] To use mirror equation, we must note the sign rules involved in this equation: 

• $f<0$ for convex mirror and $f>0$ for concave mirror.
• The image distance is always formed behind the convex mirror so $d_i<0$. 
• In a concave mirror, if the image is formed on the same side of the object so $d_i>0$ otherwise $d_i<0$ must be inserted. 

In this problem, the mirror is concave so focal length must be put with a plus sign $f>0$ in the mirror equation. \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{20}&=\frac{1}{d_i}+\frac{1}{6}\\ \\ \Rightarrow \frac{1}{d_i}&=\frac{1}{20}-\frac{1}{6}\\\\&=\frac{6-20}{20\times 6}\\ \\ &=\frac{-14}{20\times 6}\end{align*} Flipping both sides of above relation, we get \[d_i=-\frac{120}{14}=8.57\quad {\rm cm}\] As you can see, we obtained a negative value for image distance for an object in front of a concave mirror. Thus, we conclude that the image must be formed on the opposite side of the mirror, or in other words, behind the mirror. 

This image which is formed on the opposite side of the object is called a virtual image. 

Therefore, the image of the above pencil is located about 9 cm behind the mirror. 

(c) In the following figure, using two rays we obtained the image of the pencil. 

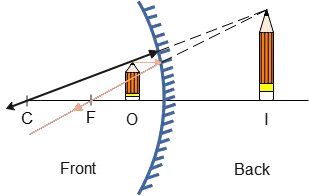
(d) In this problem, the object sits between the focal point and the concave mirror. As the ray diagram above showed, once there was such a case, we obtain a virtual, upright, and magnified image. But how much bigger? see next problem. 

Problem (2): A candle 6 cm tall is placed at a distance of 8 cm in front of a concave mirror whose radius of curvature is 20 cm. Determine the position, size, orientation, and nature (real or virtual) of the image. 

Solution : Known data is object' height $h_o=6\,{\rm cm}$, object distance $d_o=10\,{\rm cm}$, and the radius of curvature of the mirror $R=20\,{\rm cm}$. The focal length is obtained as below \[f=\frac R2=10\quad {\rm cm}\] As you can see, $d_o<f$ that is the object is located between the focal point and the concave mirror. In such cases, we have a virtual, upright, and bigger image (see the previous problem). 

Applying the mirror equation get the position of the image $d_i$ as below \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{10}&=\frac{1}{d_i}+\frac{1}{8}\\ \\ \Rightarrow \frac{1}{d_i}&=\frac{1}{10}-\frac{1}{8}\\\\&=\frac{8-10}{10\times 8}\\ \\ &=\frac{-2}{80}\end{align*} Reversing both sides of the above, we have $d_i=-40\,{\rm cm}$. Because image distance $d_i$ is negative, the image is on the opposite side of the mirror and hence is virtual. 

To quantify how much bigger the image is in the curved mirrors, we use the magnification formula for curved mirrors as below \[M=\frac{h_i}{h_o}=-\frac{d_i}{d_o}\] Where $h_i$, $h_o$ are the image and object heights. \[M=-\frac{d_i}{d_o}=-\frac{-40}{8}=5\] Thus, the object is magnified as big as 5 times. 

Problem (3): A certain concave spherical mirror has a focal length of 10 cm. An object is located 10 cm in front of it. Find the properties of the image. 

Solution : Here, the object is at the focal point. Use the mirror equation to find the image position as below \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{10}&=\frac{1}{d_i}+\frac{1}{10}\\ \\ \frac{1}{d_i}&=0 \\ \\ \Rightarrow d_i&=\infty \end{align*} Thus, the image is formed at infinity!. Using the magnification formula, we can see that it is also infinite. 

From this problem, we conclude that when an object is placed at the focal point, its image is formed at infinity with infinite in size. 

Problem (4): In front of a concave mirror whose radius of curvature is 20 cm we place a candle, 5 cm tall, at a distance of 25 cm away from it. Determine (a) the position,(b) the size, and (c) the nature (real or virtual) and orientation of the image. 

Solution : All we need to find the image properties is to apply the mirror equation and magnification formula. In this problem, the radius of curvature of the concave curved mirror is given which is related to the focal length by the following formula \[f=\frac R2=\frac {20}{2}=10\,{\rm cm}\] The object is placed outside the center of the curvature of the concave mirror because $d_o>2f$. Now, we want to find the properties of the image formed by this object in this position. 

(a) First of all, using the mirror equation we find the image distance from the concave mirror but recall that, according to mirror sign rules, for the concave mirror, the focal length must be inserted as $f>0$. \begin{align*} \frac{1}{f}&=\frac{1}{d_i}+\frac{1}{d_o}\\ \\ \frac{1}{10}&=\frac{1}{d_i}+\frac{1}{25}\\ \\ \frac{1}{d_i}&=\frac{1}{10}-\frac{1}{25}\\\\&=\frac{25-10}{10\times 25}\\\\&=\frac{15}{25} \\ \\ \Rightarrow d_i&=\frac{25}{15}=16.7\,{\rm cm} \end{align*} Because $d_i>0$, the image is in front of the mirror and is real (on the same side of the object). In other words, the image is formed between the focal point and the center of the curvature. 

(b) Magnification in curved mirrors is the ratio of the image size to the object size or the ratio of the image distance to the object distance with a negative. \[M=\frac{h_i}{h_o}=-\frac{d_i}{d_o}\]

From the first expression, we can find the magnification of the mirror as \[M=-\frac{d_i}{d_o}=\frac{16.7}{25}=-0.6\] The image is 0.6 the size of the object. 

The image height is also obtained by the second expression as below \begin{align*} M&=\frac{h_i}{h_o}\\\\ -0.6&=\frac{h_i}{5}\\\\ \Rightarrow  h_i&=(-0.6)(5)=-3\,{\rm cm}\end{align*} The minus sign indicates that the image is inverted. 

(c) Because $d_i>0$, the image is real. Since the magnification is negative $M<0$, the image is inverted. 

All of the above findings can also be obtained by a concave mirror ray diagram as shown in the figure below. 

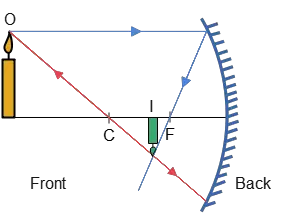
The notes we learn from this problem are that when an object is placed outside the center of curvature of a concave mirror, then the image is real, inverted, reduced in size, and is formed between focal point $f$ and center of curvature $C$. 

For more practicing, you can also check out the following pages Converging Lens Problems with Solution Diverging Lens Problems with Solution  

Author : Dr. Ali Nemati Date Published: 5/14/2021  

© 2015 All rights reserved. by Physexams.com

• TPC and eLearning
• What's NEW at TPC?
• Read Watch Interact
• Practice Review Test
• Teacher-Tools
• Request a Demo
• Get A Quote
• Subscription Selection
• Seat Calculator
• Ad Free Account
• Edit Profile Settings
• Metric Conversions Questions
• Metric System Questions
• Metric Estimation Questions
• Significant Digits Questions
• Proportional Reasoning
• Acceleration
• Distance-Displacement
• Dots and Graphs
• Graph That Motion
• Match That Graph
• Name That Motion
• Motion Diagrams
• Pos'n Time Graphs Numerical
• Pos'n Time Graphs Conceptual
• Up And Down - Questions
• Balanced vs. Unbalanced Forces
• Change of State
• Force and Motion
• Mass and Weight
• Match That Free-Body Diagram
• Net Force (and Acceleration) Ranking Tasks
• Newton's Second Law
• Normal Force Card Sort
• Recognizing Forces
• Air Resistance and Skydiving
• Solve It! with Newton's Second Law
• Which One Doesn't Belong?
• Component Addition Questions
• Head-to-Tail Vector Addition
• Projectile Mathematics
• Trajectory - Angle Launched Projectiles
• Trajectory - Horizontally Launched Projectiles
• Vector Addition
• Vector Direction
• Which One Doesn't Belong? Projectile Motion
• Forces in 2-Dimensions
• Being Impulsive About Momentum
• Explosions - Law Breakers
• Hit and Stick Collisions - Law Breakers
• Case Studies: Impulse and Force
• Impulse-Momentum Change Table
• Keeping Track of Momentum - Hit and Stick
• Keeping Track of Momentum - Hit and Bounce
• What's Up (and Down) with KE and PE?
• Energy Conservation Questions
• Energy Dissipation Questions
• Energy Ranking Tasks
• LOL Charts (a.k.a., Energy Bar Charts)
• Match That Bar Chart
• Words and Charts Questions
• Name That Energy
• Stepping Up with PE and KE Questions
• Case Studies - Circular Motion
• Circular Logic
• Forces and Free-Body Diagrams in Circular Motion
• Gravitational Field Strength
• Universal Gravitation
• Angular Position and Displacement
• Linear and Angular Velocity
• Angular Acceleration
• Rotational Inertia
• Balanced vs. Unbalanced Torques
• Getting a Handle on Torque
• Torque-ing About Rotation
• Properties of Matter
• Fluid Pressure
• Buoyant Force
• Sinking, Floating, and Hanging
• Pascal's Principle
• Flow Velocity
• Bernoulli's Principle
• Balloon Interactions
• Charge and Charging
• Charge Interactions
• Charging by Induction
• Conductors and Insulators
• Coulombs Law
• Electric Field
• Electric Field Intensity
• Polarization
• Case Studies: Electric Power
• Know Your Potential
• Light Bulb Anatomy
• I = ∆V/R Equations as a Guide to Thinking
• Parallel Circuits - ∆V = I•R Calculations
• Resistance Ranking Tasks
• Series Circuits - ∆V = I•R Calculations
• Series vs. Parallel Circuits
• Equivalent Resistance
• Period and Frequency of a Pendulum
• Pendulum Motion: Velocity and Force
• Energy of a Pendulum
• Period and Frequency of a Mass on a Spring
• Horizontal Springs: Velocity and Force
• Vertical Springs: Velocity and Force
• Energy of a Mass on a Spring
• Decibel Scale
• Frequency and Period
• Closed-End Air Columns
• Name That Harmonic: Strings
• Rocking the Boat
• Wave Basics
• Matching Pairs: Wave Characteristics
• Wave Interference
• Waves - Case Studies
• Color Addition and Subtraction
• Color Filters
• If This, Then That: Color Subtraction
• Light Intensity
• Color Pigments
• Converging Lenses
• Curved Mirror Images
• Law of Reflection
• Refraction and Lenses
• Total Internal Reflection
• Who Can See Who?
• Lab Equipment
• Lab Procedures
• Formulas and Atom Counting
• Atomic Models
• Bond Polarity
• Entropy Questions
• Cell Voltage Questions
• Heat of Formation Questions
• Reduction Potential Questions
• Oxidation States Questions
• Measuring the Quantity of Heat
• Hess's Law
• Oxidation-Reduction Questions
• Galvanic Cells Questions
• Thermal Stoichiometry
• Molecular Polarity
• Quantum Mechanics
• Balancing Chemical Equations
• Bronsted-Lowry Model of Acids and Bases
• Classification of Matter
• Collision Model of Reaction Rates
• Density Ranking Tasks
• Dissociation Reactions
• Complete Electron Configurations
• Elemental Measures
• Enthalpy Change Questions
• Equilibrium Concept
• Equilibrium Constant Expression
• Equilibrium Calculations - Questions
• Equilibrium ICE Table
• Intermolecular Forces Questions
• Ionic Bonding
• Lewis Electron Dot Structures
• Limiting Reactants
• Line Spectra Questions
• Mass Stoichiometry
• Measurement and Numbers
• Metals, Nonmetals, and Metalloids
• Metric Estimations
• Metric System
• Molarity Ranking Tasks
• Mole Conversions
• Name That Element
• Names to Formulas
• Names to Formulas 2
• Nuclear Decay
• Particles, Words, and Formulas
• Periodic Trends
• Precipitation Reactions and Net Ionic Equations
• Pressure Concepts
• Pressure-Temperature Gas Law
• Pressure-Volume Gas Law
• Chemical Reaction Types
• Significant Digits and Measurement
• States Of Matter Exercise
• Stoichiometry Law Breakers
• Stoichiometry - Math Relationships
• Subatomic Particles
• Spontaneity and Driving Forces
• Gibbs Free Energy
• Volume-Temperature Gas Law
• Acid-Base Properties
• Energy and Chemical Reactions
• Chemical and Physical Properties
• Valence Shell Electron Pair Repulsion Theory
• Writing Balanced Chemical Equations
• Mission CG1
• Mission CG10
• Mission CG2
• Mission CG3
• Mission CG4
• Mission CG5
• Mission CG6
• Mission CG7
• Mission CG8
• Mission CG9
• Mission EC1
• Mission EC10
• Mission EC11
• Mission EC12
• Mission EC2
• Mission EC3
• Mission EC4
• Mission EC5
• Mission EC6
• Mission EC7
• Mission EC8
• Mission EC9
• Mission RL1
• Mission RL2
• Mission RL3
• Mission RL4
• Mission RL5
• Mission RL6
• Mission KG7
• Mission RL8
• Mission KG9
• Mission RL10
• Mission RL11
• Mission RM1
• Mission RM2
• Mission RM3
• Mission RM4
• Mission RM5
• Mission RM6
• Mission RM8
• Mission RM10
• Mission LC1
• Mission RM11
• Mission LC2
• Mission LC3
• Mission LC4
• Mission LC5
• Mission LC6
• Mission LC8
• Mission SM1
• Mission SM2
• Mission SM3
• Mission SM4
• Mission SM5
• Mission SM6
• Mission SM8
• Mission SM10
• Mission KG10
• Mission SM11
• Mission KG2
• Mission KG3
• Mission KG4
• Mission KG5
• Mission KG6
• Mission KG8
• Mission KG11
• Mission F2D1
• Mission F2D2
• Mission F2D3
• Mission F2D4
• Mission F2D5
• Mission F2D6
• Mission KC1
• Mission KC2
• Mission KC3
• Mission KC4
• Mission KC5
• Mission KC6
• Mission KC7
• Mission KC8
• Mission AAA
• Mission SM9
• Mission LC7
• Mission LC9
• Mission NL1
• Mission NL2
• Mission NL3
• Mission NL4
• Mission NL5
• Mission NL6
• Mission NL7
• Mission NL8
• Mission NL9
• Mission NL10
• Mission NL11
• Mission NL12
• Mission MC1
• Mission MC10
• Mission MC2
• Mission MC3
• Mission MC4
• Mission MC5
• Mission MC6
• Mission MC7
• Mission MC8
• Mission MC9
• Mission RM7
• Mission RM9
• Mission RL7
• Mission RL9
• Mission SM7
• Mission SE1
• Mission SE10
• Mission SE11
• Mission SE12
• Mission SE2
• Mission SE3
• Mission SE4
• Mission SE5
• Mission SE6
• Mission SE7
• Mission SE8
• Mission SE9
• Mission VP1
• Mission VP10
• Mission VP2
• Mission VP3
• Mission VP4
• Mission VP5
• Mission VP6
• Mission VP7
• Mission VP8
• Mission VP9
• Mission WM1
• Mission WM2
• Mission WM3
• Mission WM4
• Mission WM5
• Mission WM6
• Mission WM7
• Mission WM8
• Mission WE1
• Mission WE10
• Mission WE2
• Mission WE3
• Mission WE4
• Mission WE5
• Mission WE6
• Mission WE7
• Mission WE8
• Mission WE9
• Vector Walk Interactive
• Name That Motion Interactive
• Kinematic Graphing 1 Concept Checker
• Kinematic Graphing 2 Concept Checker
• Graph That Motion Interactive
• Two Stage Rocket Interactive
• Rocket Sled Concept Checker
• Force Concept Checker
• Free-Body Diagrams Concept Checker
• Free-Body Diagrams The Sequel Concept Checker
• Skydiving Concept Checker
• Elevator Ride Concept Checker
• Vector Addition Concept Checker
• Vector Walk in Two Dimensions Interactive
• Name That Vector Interactive
• River Boat Simulator Concept Checker
• Projectile Simulator 2 Concept Checker
• Projectile Simulator 3 Concept Checker
• Hit the Target Interactive
• Turd the Target 1 Interactive
• Turd the Target 2 Interactive
• Balance It Interactive
• Go For The Gold Interactive
• Egg Drop Concept Checker
• Fish Catch Concept Checker
• Exploding Carts Concept Checker
• Collision Carts - Inelastic Collisions Concept Checker
• Its All Uphill Concept Checker
• Stopping Distance Concept Checker
• Chart That Motion Interactive
• Roller Coaster Model Concept Checker
• Uniform Circular Motion Concept Checker
• Horizontal Circle Simulation Concept Checker
• Vertical Circle Simulation Concept Checker
• Race Track Concept Checker
• Gravitational Fields Concept Checker
• Orbital Motion Concept Checker
• Angular Acceleration Concept Checker
• Balance Beam Concept Checker
• Torque Balancer Concept Checker
• Aluminum Can Polarization Concept Checker
• Charging Concept Checker
• Name That Charge Simulation
• Coulomb's Law Concept Checker
• Electric Field Lines Concept Checker
• Put the Charge in the Goal Concept Checker
• Circuit Builder Concept Checker (Series Circuits)
• Circuit Builder Concept Checker (Parallel Circuits)
• Circuit Builder Concept Checker (∆V-I-R)
• Circuit Builder Concept Checker (Voltage Drop)
• Equivalent Resistance Interactive
• Pendulum Motion Simulation Concept Checker
• Mass on a Spring Simulation Concept Checker
• Particle Wave Simulation Concept Checker
• Boundary Behavior Simulation Concept Checker
• Slinky Wave Simulator Concept Checker
• Simple Wave Simulator Concept Checker
• Wave Addition Simulation Concept Checker
• Standing Wave Maker Simulation Concept Checker
• Color Addition Concept Checker
• Painting With CMY Concept Checker
• Stage Lighting Concept Checker
• Filtering Away Concept Checker
• InterferencePatterns Concept Checker
• Young's Experiment Interactive
• Plane Mirror Images Interactive
• Who Can See Who Concept Checker
• Optics Bench (Mirrors) Concept Checker
• Name That Image (Mirrors) Interactive
• Refraction Concept Checker
• Total Internal Reflection Concept Checker
• Optics Bench (Lenses) Concept Checker
• Making an Ion Concept Checker
• Phase Changes Concept Checker
• Kinematics Preview
• Velocity Time Graphs Preview
• Moving Cart on an Inclined Plane Preview
• Stopping Distance Preview
• Cart, Bricks, and Bands Preview
• Fan Cart Study Preview
• Friction Preview
• Coffee Filter Lab Preview
• Friction, Speed, and Stopping Distance Preview
• Up and Down Preview
• Projectile Range Preview
• Ballistics Preview
• Juggling Preview
• Marshmallow Launcher Preview
• Air Bag Safety Preview
• Colliding Carts Preview
• Collisions Preview
• Engineering Safer Helmets Preview
• Push the Plow Preview
• Its All Uphill Preview
• Energy on an Incline Preview
• Modeling Roller Coasters Preview
• Hot Wheels Stopping Distance Preview
• Ball Bat Collision Preview
• Energy in Fields Preview
• Weightlessness Training Preview
• Roller Coaster Loops Preview
• Universal Gravitation Preview
• Keplers Laws Preview
• Kepler's Third Law Preview
• Charge Interactions Preview
• Sticky Tape Experiments Preview
• Wire Gauge Preview
• Voltage, Current, and Resistance Preview
• Light Bulb Resistance Preview
• Series and Parallel Circuits Preview
• Thermal Equilibrium Preview
• Linear Expansion Preview
• Heating Curves Preview
• Electricity and Magnetism - Part 1 Preview
• Electricity and Magnetism - Part 2 Preview
• Vibrating Mass on a Spring Preview
• Period of a Pendulum Preview
• Wave Speed Preview
• Slinky-Experiments Preview
• Standing Waves in a Rope Preview
• Sound as a Pressure Wave Preview
• DeciBel Scale Preview
• DeciBels, Phons, and Sones Preview
• Sound of Music Preview
• Shedding Light on Light Bulbs Preview
• Models of Light Preview
• Electromagnetic Radiation Preview
• Electromagnetic Spectrum Preview
• EM Wave Communication Preview
• Digitized Data Preview
• Light Intensity Preview
• Concave Mirrors Preview
• Object Image Relations Preview
• Snells Law Preview
• Reflection vs. Transmission Preview
• Magnification Lab Preview
• Reactivity Preview
• Ions and the Periodic Table Preview
• Periodic Trends Preview
• Chemical Reactions Preview
• Intermolecular Forces Preview
• Melting Points and Boiling Points Preview
• Bond Energy and Reactions Preview
• Reaction Rates Preview
• Ammonia Factory Preview
• Stoichiometry Preview
• Nuclear Chemistry Preview
• Gaining Teacher Access
• Task Tracker Directions
• Conceptual Physics Course
• On-Level Physics Course
• Honors Physics Course
• Chemistry Concept Builders
• All Chemistry Resources
• Users Voice
• Tasks and Classes
• Webinars and Trainings
• Subscription
• Subscription Locator
• 1-D Kinematics
• Newton's Laws
• Vectors - Motion and Forces in Two Dimensions
• Momentum and Its Conservation
• Work and Energy
• Circular Motion and Satellite Motion
• Thermal Physics
• Static Electricity
• Electric Circuits
• Vibrations and Waves
• Sound Waves and Music
• Light and Color
• Reflection and Mirrors
• Measurement and Calculations
• Elements, Atoms, and Ions
• Compounds,Names, and Formulas
• The Modern Atomic Model
• Chemical Bonding
• The Mole and its Applications
• Chemical Reactions
• Stoichiometry
• About the Physics Interactives
• Task Tracker
• Usage Policy
• Newtons Laws
• Vectors and Projectiles
• Forces in 2D
• Momentum and Collisions
• Circular and Satellite Motion
• Balance and Rotation
• Electromagnetism
• Waves and Sound
• Atomic Physics
• Forces in Two Dimensions
• Work, Energy, and Power
• Circular Motion and Gravitation
• Sound Waves
• 1-Dimensional Kinematics
• Circular, Satellite, and Rotational Motion
• Einstein's Theory of Special Relativity
• Waves, Sound and Light
• QuickTime Movies
• About the Concept Builders
• Pricing For Schools
• Directions for Version 2
• Measurement and Units
• Relationships and Graphs
• Rotation and Balance
• Vibrational Motion
• Reflection and Refraction
• Teacher Accounts
• Kinematic Concepts
• Kinematic Graphing
• Wave Motion
• Sound and Music
• About CalcPad
• 1D Kinematics
• Vectors and Forces in 2D
• Simple Harmonic Motion
• Rotational Kinematics
• Rotation and Torque
• Rotational Dynamics
• Electric Fields, Potential, and Capacitance
• Transient RC Circuits
• Light Waves
• Units and Measurement
• Molarity and Solutions
• Thermal Chemistry
• Acids and Bases
• Kinetics and Equilibrium
• Solution Equilibria
• Oxidation-Reduction
• Nuclear Chemistry
• Newton's Laws of Motion
• Work and Energy Packet
• Static Electricity Review
• NGSS Alignments
• 1D-Kinematics
• Projectiles
• Circular Motion
• Magnetism and Electromagnetism
• Graphing Practice
• About the ACT
• ACT Preparation
• For Teachers
• Other Resources
• Solutions Guide
• Solutions Guide Digital Download
• Solution Guide Corrections
• Motion in One Dimension
• Work, Energy and Power
• Chemistry of Matter
• Measurement and the Metric System
• Early Atomic Models
• Names and Formulas
• The Modern Model of the Atom
• Algebra Based On-Level Physics
• Honors Physics
• Conceptual Physics
• Other Tools
• Frequently Asked Questions
• Purchasing the Download
• Purchasing the Digital Download
• About the NGSS Corner
• NGSS Search
• Force and Motion DCIs - High School
• Energy DCIs - High School
• Wave Applications DCIs - High School
• Force and Motion PEs - High School
• Energy PEs - High School
• Wave Applications PEs - High School
• Crosscutting Concepts
• The Practices
• Physics Topics
• NGSS Corner: Activity List
• NGSS Corner: Infographics
• About the Toolkits
• Position-Velocity-Acceleration
• Position-Time Graphs
• Velocity-Time Graphs
• Newton's First Law
• Newton's Second Law
• Newton's Third Law
• Terminal Velocity
• Projectile Motion
• Forces in 2 Dimensions
• Impulse and Momentum Change
• Momentum Conservation
• Work-Energy Fundamentals
• Work-Energy Relationship
• Roller Coaster Physics
• Satellite Motion
• Electric Fields
• Circuit Concepts
• Series Circuits
• Parallel Circuits
• Describing-Waves
• Wave Behavior Toolkit
• Standing Wave Patterns
• Resonating Air Columns
• Wave Model of Light
• Plane Mirrors
• Curved Mirrors
• Teacher Guide
• Using Lab Notebooks
• Current Electricity
• Light Waves and Color
• Reflection and Ray Model of Light
• Refraction and Ray Model of Light
• Teacher Resources
• Subscriptions

• Newton's Laws
• Einstein's Theory of Special Relativity
• About Concept Checkers
• School Pricing
• Newton's Laws of Motion
• Newton's First Law
• Newton's Third Law

Ray Optics: Reflection and Mirrors

Reflection and mirrors: problem set overview.

There are 15 ready-to-use problem sets on the topic of Reflection and Mirrors. The problems target your ability to use the law of reflection, to understand the relationship between image distance and object distance for plane mirrors, and to use the mirror equation and magnification ratio to solve problems that relate object and image characteristics to the focal length of concave and convex mirrors. Problems range in difficulty from the very easy and straight-forward to the very difficult and complex.   

• The Law of Reflection

Light rays follow a rather predictable pattern when it comes to reflection off a plane mirror surface. The angle at which the light ray approaches the mirror surface is equal to the angle at which it departs from the mirror. This is known as the law of reflection . In physics, the angles of approach are measured with respect to the normal line to the surface. The normal line is the imaginary line that is perpendicular to the mirror at the point that the light ray strikes the mirror. The angle between the normal line and the approaching or incident ray is known as the angle of incidence . Similarly, the angle between the reflected ray and the same normal line is known as the angle of reflection . According to the law of reflection, the angle of incidence is equal to the angle of reflection. A more detailed and exhaustive discussion of the law of reflection and associated terms can be found at The Physics Classroom Tutorial . Alternatively, you can try our video titled The Law of Reflection .  

Characteristics of Plane Mirror Images

Objects placed in front of plane mirrors will have a corresponding image located behind the mirror. The distance from the image to the mirror is always identical to the distance from the object to the mirror. So if a person stands 2.0 meters in front of the mirror, then the image will be located an identical 2.0 meters behind the mirror. Such an image is a virtual image . When viewing such a virtual image in the mirror, it would seem as though light is coming from a location 2.0 meters behind the mirror. If you were to walk behind the mirror and look at this so-called virtual image location, there would be nothing physical present there. It only seems to the observer as thought light is coming from this location to the eye when viewing the image of the person in the mirror. A more detailed and exhaustive discussion of plane mirror image characteristics can be found at The Physics Classroom Tutorial . Alternatively, you can try our video titled Image Formation for Plane Mirrors .  

Curved Mirror Mathematics

Most of the problems in this unit pertain to curved mirrors - both the concave and the convex varieties.The two equations of relevance for these problems are the mirror equation and the magnification equation. The mirror equation relates the image distance to the object distance and the focal length. The mirror equation is

1/f = 1/d o + 1/d i

The variable d o represents the object distance or the distance between the mirror surface and the object. The variable d i represents the image distance or the distance between the mirror surface and the image. The variable f stands for the focal length of the mirror. In some problems, the focal length is not stated; rather, the radius of curvature of the spherical mirror is stated. The radius of curvature ( R ) is simply twice the focal length value ( R = 2•f ). Like any equation in physics, the mirror equation can be used to solve for an unknown variable through algebraic substitution and rearrangement. Given that there are three quantities present in the mirror equation, two of them must be known in order to solve for the third unknown quantity.

A curved mirror usually causes an image to be either magnified or reduced in size relative to the size of the object. The magnification ratio is a number which expresses the amount of magnification or reduction. The magnification ratio is simply the ratio of the image size to the object size. It is often calculated using the equation

M = h i / h o

In this equation, the variable M represents the magnification, the variable h i represents the image height, and the variable h o represents the object height. It ends up that the ratio of the image to object heights is equivalent to the ratio of the image to the object distance. And so the magnification equation is often written as

M = h i / h o = - d i / d o

The negative sign in the above equation is related to what could be the most problematic aspect of this topic. The variables in these two equations can be either positive or negative. The positive and negative nature is determined by the actual characteristics of the images which are formed and the mirrors which are used in the specific problems. The table below summarizes the so-called sign conventions for the six variables of these two equations.

When reading a problem, it is important to give attention to cues within the problem in order to determine the sign on the given quantity. For example, the distance from the focal point to a mirror is often stated. This is simply a distance value corresponding to the absolute value of the focal length. Whether the focal length is positive or negative is dependent upon whether the mirror is concave or convex. A careful reading of the problem and an understanding of the sign convention on focal length (as stated in the table above) allows one to make the decision about the sign on f. As a second example, some problems describe an image being located a stated distance from a curved mirror. The stated value is simply the absolute value of the image distance. Whether the d i value is positive or negative depends upon whether the image is in front of or behind the mirror. A careful reading of the problem statement along with an understanding of the sign convention for image distance (as stated in the table above) allows one to make the decision about the sign on d i . These types of decisions are critical to your success on thes problems. Making the correct decisions has nothing to do with your mathematical skills; rather, they are tests of your conceptual understandings and your willingness to read a problem carefully and to give attention to details which may be important.

There are a few instances in this problem set in which the mirror equation must be used to solve for an unknown variable but only one of the other two variable values are known. Such problems usually have a statement of the effect: "the image is real and three times the size of the object." Such a statement reveals information about the magnification of the image. Since the ratio of the image to object height is equal to the (negative of the) ratio of the image distance to object distance, we can say that size and height can be treated synonymously. Stating that the image is three times the size of the object is stating that the ratio h i /h o is either +3 or -3. Determining whether h i /h o is +3 or -3 demands an understanding of the sign conventions (as discussed in the above table). The h o value is always positive (for our purposes). The h i value is positive for upright images and negative for inverted images. Since this statement asserts that the image is real (and thus inverted), a -3 value must be assigned to the h i /h o ratio. Since hi/ho is equal to -d i /d o , the -3 value can be equated with -d i /d o . This stream of logic allows one to write an expression for d i in terms of d o . This expression for d i in terms of d o can be substituted into the mirror equation in order to transform it into a single equation with a single unknown. Customary algebraic manipulations can then be performed in order to solve for d i or for d o .

The table below summarizes the process of transforming a verbal statement into a mathematical equation which ultimately is used to substitute into the mirror equation.

Habits of an Effective Problem-Solver

An effective problem solver by habit approaches a physics problem in a manner that reflects a collection of disciplined habits. While not every effective problem solver employs the same approach, they all have habits which they share in common. These habits are described briefly here. An effective problem-solver...

• ...reads the problem carefully and develops a mental picture of the physical situation. If needed, they sketch a simple diagram of the physical situation to help visualize it.
• ...identifies and records the known and unknown quantities in an organized manner. Equates given values to the symbols used to represent the corresponding quantity - e.g., d o = 24.2 cm; d i = 16.8 cm; f = ???.
• ...plots a strategy for solving for the unknown quantity; the strategy will typically center around the use of physics equations and be heavily dependent upon an understanding of physics principles.
• ...identifies the appropriate formula(s) to use, often times writing them down. Where needed, they perform the needed conversion of quantities into the proper unit.
• ...performs substitutions and algebraic manipulations in order to solve for the unknown quantity.

Read more...  

Additional Readings/Study Aids:

The following pages from The Physics Classroom Tutorial may serve to be useful in assisting you in the understanding of the concepts and mathematics associated with these problems.

• Image Characteristics for Plane Mirrors
• What Portion of a Mirror is Required to View an Image?
• Image Characteristics for Concave Mirrors
• The Mirror Equation - Concave Mirrors
• Image Characteristics for Convex Mirrors
• The Mirror Equation - Convex Mirrors

Watch a Video

We have developed and continue to develop Video Tutorials on introductory physics topics. You can find these videos on our YouTube channel . We have an entire Playlist on the topic of Reflection and Mirrors .