hungarian method for assignment problem example

Hungarian Method Examples

Now we will examine a few highly simplified illustrations of Hungarian Method for solving an assignment problem .

Later in the chapter, you will find more practical versions of assignment models like Crew assignment problem , Travelling salesman problem , etc.

Example-1, Example-2

Example 1: Hungarian Method

The Funny Toys Company has four men available for work on four separate jobs. Only one man can work on any one job. The cost of assigning each man to each job is given in the following table. The objective is to assign men to jobs in such a way that the total cost of assignment is minimum.

This is a minimization example of assignment problem . We will use the Hungarian Algorithm to solve this problem.

Identify the minimum element in each row and subtract it from every element of that row. The result is shown in the following table.

"A man has one hundred dollars and you leave him with two dollars, that's subtraction." -Mae West

On small screens, scroll horizontally to view full calculation

Identify the minimum element in each column and subtract it from every element of that column.

Make the assignments for the reduced matrix obtained from steps 1 and 2 in the following way:

For every zero that becomes assigned, cross out (X) all other zeros in the same row and the same column.
If for a row and a column, there are two or more zeros and one cannot be chosen by inspection, choose the cell arbitrarily for assignment.

An optimal assignment is found, if the number of assigned cells equals the number of rows (and columns). In case you have chosen a zero cell arbitrarily, there may be alternate optimal solutions. If no optimal solution is found, go to step 5.

Use Horizontal Scrollbar to View Full Table Calculation

Draw the minimum number of vertical and horizontal lines necessary to cover all the zeros in the reduced matrix obtained from step 3 by adopting the following procedure:

Mark all the rows that do not have assignments.
Mark all the columns (not already marked) which have zeros in the marked rows.
Mark all the rows (not already marked) that have assignments in marked columns.
Repeat steps 5 (ii) and (iii) until no more rows or columns can be marked.
Draw straight lines through all unmarked rows and marked columns.

You can also draw the minimum number of lines by inspection.

Select the smallest element (i.e., 1) from all the uncovered elements. Subtract this smallest element from all the uncovered elements and add it to the elements, which lie at the intersection of two lines. Thus, we obtain another reduced matrix for fresh assignment.

Now again make the assignments for the reduced matrix.

Final Table: Hungarian Method

Since the number of assignments is equal to the number of rows (& columns), this is the optimal solution.

The total cost of assignment = A1 + B4 + C2 + D3

Substituting values from original table: 20 + 17 + 17 + 24 = Rs. 78.

Share This Article

Operations Research Simplified Back Next

Goal programming Linear programming Simplex Method Transportation Problem

Procedure, Example Solved Problem | Operations Research - Solution of assignment problems (Hungarian Method) | 12th Business Maths and Statistics : Chapter 10 : Operations Research

Chapter: 12th business maths and statistics : chapter 10 : operations research.

Solution of assignment problems (Hungarian Method)

First check whether the number of rows is equal to the numbers of columns, if it is so, the assignment problem is said to be balanced.

Step :1 Choose the least element in each row and subtract it from all the elements of that row.

Step :2 Choose the least element in each column and subtract it from all the elements of that column. Step 2 has to be performed from the table obtained in step 1.

Step:3 Check whether there is atleast one zero in each row and each column and make an assignment as follows.

hungarian method for assignment problem example

Step :4 If each row and each column contains exactly one assignment, then the solution is optimal.

Example 10.7

Solve the following assignment problem. Cell values represent cost of assigning job A, B, C and D to the machines I, II, III and IV.

Here the number of rows and columns are equal.

∴ The given assignment problem is balanced. Now let us find the solution.

Step 1: Select a smallest element in each row and subtract this from all the elements in its row.

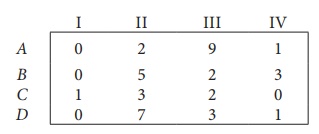
Look for atleast one zero in each row and each column.Otherwise go to step 2.

Step 2: Select the smallest element in each column and subtract this from all the elements in its column.

Since each row and column contains atleast one zero, assignments can be made.

Step 3 (Assignment):

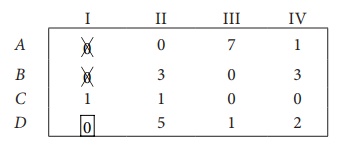
Thus all the four assignments have been made. The optimal assignment schedule and total cost is

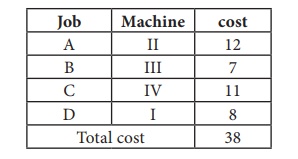
The optimal assignment (minimum) cost

Example 10.8

Consider the problem of assigning five jobs to five persons. The assignment costs are given as follows. Determine the optimum assignment schedule.

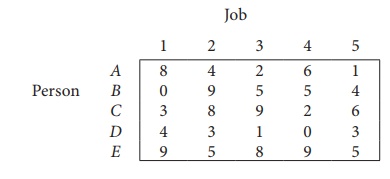
∴ The given assignment problem is balanced.

Now let us find the solution.

The cost matrix of the given assignment problem is

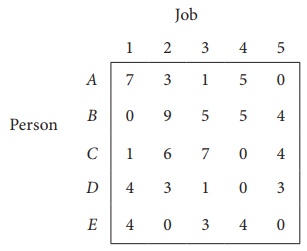
Column 3 contains no zero. Go to Step 2.

Thus all the five assignments have been made. The Optimal assignment schedule and total cost is

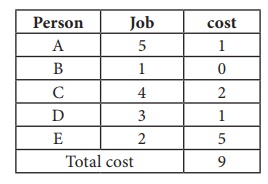
The optimal assignment (minimum) cost = ` 9

Example 10.9

Solve the following assignment problem.

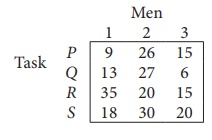
Since the number of columns is less than the number of rows, given assignment problem is unbalanced one. To balance it , introduce a dummy column with all the entries zero. The revised assignment problem is

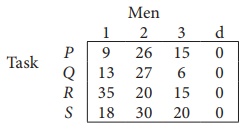
Here only 3 tasks can be assigned to 3 men.

Step 1: is not necessary, since each row contains zero entry. Go to Step 2.

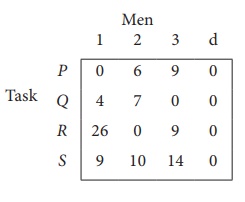
Step 3 (Assignment) :

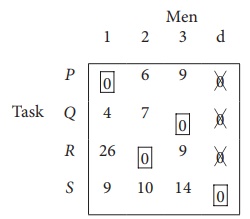
Since each row and each columncontains exactly one assignment,all the three men have been assigned a task. But task S is not assigned to any Man. The optimal assignment schedule and total cost is

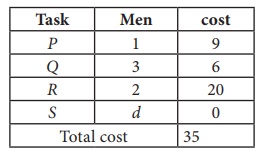
The optimal assignment (minimum) cost = ₹ 35

The Hungarian algorithm: An example

We consider an example where four jobs (J1, J2, J3, and J4) need to be executed by four workers (W1, W2, W3, and W4), one job per worker. The matrix below shows the cost of assigning a certain worker to a certain job. The objective is to minimize the total cost of the assignment.

Below we will explain the Hungarian algorithm using this example. Note that a general description of the algorithm can be found here .

Step 1: Subtract row minima

We start with subtracting the row minimum from each row. The smallest element in the first row is, for example, 69. Therefore, we substract 69 from each element in the first row. The resulting matrix is:

Step 2: Subtract column minima

Similarly, we subtract the column minimum from each column, giving the following matrix:

Step 3: Cover all zeros with a minimum number of lines

We will now determine the minimum number of lines (horizontal or vertical) that are required to cover all zeros in the matrix. All zeros can be covered using 3 lines:

Step 4: Create additional zeros

First, we find that the smallest uncovered number is 6. We subtract this number from all uncovered elements and add it to all elements that are covered twice. This results in the following matrix:

Now we return to Step 3.

Again, We determine the minimum number of lines required to cover all zeros in the matrix. Now there are 4 lines required:

Because the number of lines required (4) equals the size of the matrix ( n =4), an optimal assignment exists among the zeros in the matrix. Therefore, the algorithm stops.

The optimal assignment

The following zeros cover an optimal assignment:

This corresponds to the following optimal assignment in the original cost matrix:

Thus, worker 1 should perform job 3, worker 2 job 2, worker 3 job 1, and worker 4 should perform job 4. The total cost of this optimal assignment is to 69 + 37 + 11 + 23 = 140.

Solve your own problem online