scientific notation homework

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Pre-Algebra >
• Scientific Notation

Scientific Notation Worksheets

Scientific notation is a smart way of writing huge whole numbers and too small decimal numbers. This page contains worksheets based on rewriting whole numbers or decimals in scientific notation and rewriting scientific notation form to standard form. This set of printable worksheets is specially designed for students of grade 6, grade 7, grade 8, and high school. Access some of them for free!

Scientific Notation - Positive Exponents

Express in Scientific Notation

Each pdf worksheet contains 14 problems rewriting whole numbers to scientific notation. Easy level has whole numbers up to 5-digits; Moderate level has more than 5-digit numbers.

• Download the set

Express in Standard Notation

Students of 6th grade need to express each scientific notation in standard notation. An example is provided in each worksheet.

Both Standard and Scientific Notations

Each printable worksheet contains expressing numbers in both scientific and standard form.

Scientific Notation - Negative Exponents

Rewrite in Scientific Notation

Rewrite the given decimals in scientific notation. Move the decimal point to the left until you get the first non-zero digit. The number of steps you moved represent the power (index) of 10.

Rewrite in Standard Notation

In this set of pdf worksheets, express each number in standard notation. Easy level has indices more than -5; Moderate level has indices less than -4.

Each worksheet has ten problems expressing decimals in both standard and scientific notation.

Scientific Notation - Mixed Exponents

Convert to Scientific Notation

The printable worksheets in this section contain expressing both whole numbers and decimals in scientific notation.

Convert to Standard Notation

The exponent in each scientific notation can be either positive or negative.

This section of pdf worksheets gives the complete review in rewriting numbers in both standard and scientific notation. Both positive and negative exponents included.

Comparing Numbers in Scientific Notation

Call upon your inner math maestro as you sail through figuring out which of the given numbers in scientific notation is greater than, less than, or equal to the other.

Scientific Notation - Math Operations

Addition and Subtraction

This section reinforces the knowledge in adding and subtracting numbers in scientific notation.

Multiplication and Division

Use laws of exponents (indices) to multiply and divide the expressions. Express the final answer in scientific notation.

Simplify the Expression

Each worksheet gives the complete review in performing operations with scientific notations, making it ideal for 7th grade, 8th grade, and high school students.

Related Worksheets

» Exponents

» Logarithms

» Multiplying Decimals by Powers of Ten

» Dividing Decimals by Powers of Ten

Become a Member

Membership Information

Printing Help

How to Use Online Worksheets

How to Use Printable Worksheets

Privacy Policy

Terms of Use

Copyright © 2024 - Math Worksheets 4 Kids

This is a members-only feature!

Scientific Notation Worksheets (Standard to Scientific Notations)

Related Topics: More Math Worksheets More Grade 7 Math Lessons Grade 7 Math Worksheets

There are five sets of scientific notation worksheets:

• Scientific to Standard Notation
• Standard to Scientific Notation
• Multiply Scientific Numbers
• Divide Scientific Numbers
• Add & Subtract Scientific Numbers

Examples, solutions, videos, and worksheets to help Grade 7 and Grade 8 students learn how to convert from Standard Notation (Real Notation) to Scientific Notation.

How to convert from Standard Notation to Scientific Notation?

There are three sets of converting from Standard to Scientific Notation worksheets.

• Standard to Scientific Notation (positive exponents).
• Standard to Scientific Standard Notation (negative exponents)
• Standard to Scientific Standard Notation (positive & negative exponents).

These are the steps to convert a number from standard notation (real notation) to scientific notation:

• Move the decimal point so that there is one digit before the decimal point.
• Count the number of places that you moved point. This will be the exponent in the scientific notation. If you moved the decimal point to the left then the exponent is positive. If you moved the decimal point to the right then the exponent is negative.
• Express the number as a coefficient multiplied by 10 raised to the power of the exponent.

Example: Convert the number 67,000 to scientific notation.

• Move the decimal point after the first nonzero digit. From 67000. to 6.7000
• We have moved the decimal point 4 places to the left. This means the exponent will be 4.
• 67,000 = 6.7 × 10 4 (in scientific notation)

Example: Convert the number 0.00004321 to scientific notation.

• Move the decimal point after the first nonzero digit. From 0.00004321 to 4.321
• We have moved the decimal point 5 places to the right. This means the exponent will be -5.
• 0.00004321 = 4.321 × 10 -5 (in scientific notation)

Click on the following worksheet to get a printable pdf document. Scroll down the page for more Scientific Notation Worksheets .

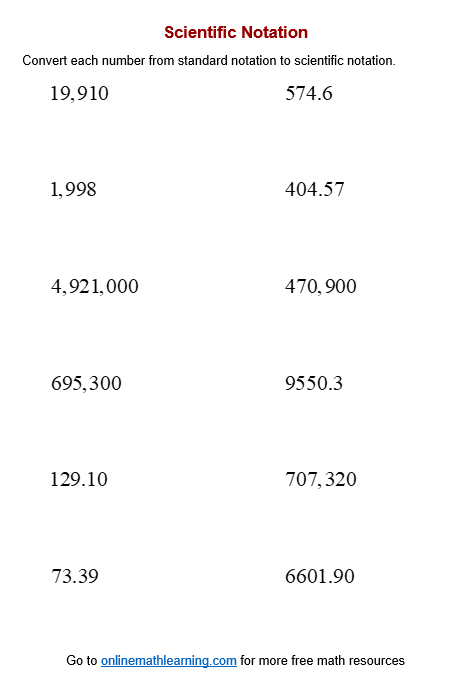
More Scientific Notation Worksheets

Printable (Answers on the second page.) Scientific Notation Worksheet #1 (positive exponents) Scientific Notation Worksheet #2 (negative exponents) Scientific Notation Worksheet #3 (positive or negative exponents)

Related Lessons & Worksheets

Scientific Notation Conversion

More Printable Worksheets

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.

Worksheet and Answer Key

• Scientific Notation
• Operations with Scientific Notation

Ultimate Math Solver (Free) Free Algebra Solver ... type anything in there!

Popular pages @ mathwarehouse.com.

Want to create or adapt books like this? Learn more about how Pressbooks supports open publishing practices.

Chapter 6: Polynomials

6.3 Scientific Notation (Homework Assignment)

Scientific notation is a convenient notation system used to represent large and small numbers. Examples of these are the mass of the sun or the mass of an electron in kilograms. Simplifying basic operations such as multiplication and division with these numbers requires using exponential properties.

Scientific notation has two parts: a number between one and nine and a power of ten, by which that number is multiplied.

[latex]\text{Scientific notation: }a \times 10^b, \text{ where }1 \le a \le 9[/latex]

The exponent tells how many times to multiply by 10. Each multiple of 10 shifts the decimal point one place. To decide which direction to move the decimal (left or right), recall that positive exponents means there is big number (larger than ten) and negative exponents means there is a small number (less than one).

Example 6.3.1

Convert 14,200 to scientific notation.

[latex]\begin{array}{rl} 1.42&\text{Put a decimal after the first nonzero number} \\ \times 10^4 & \text{The exponent is how many times the decimal moved} \\ 1.42 \times 10^4& \text{Combine to yield the solution} \end{array}[/latex]

Example 6.3.2

Convert 0.0028 to scientific notation.

[latex]\begin{array}{rl} 2.8&\text{Put a decimal after the first nonzero number} \\ \times 10^{-3}&\text{The exponent is how many times the decimal moved} \\ 2.8\times 10^{-3}&\text{Combine to yield the solution} \end{array}[/latex]

Example 6.3.3

Convert 3.21 × 10 5 to standard notation.

Starting with 3.21, Shift the decimal 5 places to the right, or multiply 3.21 by 10 5 .

321,000 is the solution.

Example 6.3.4

Convert 7.4 × 10 −3 to standard notation

Shift the decimal 3 places to the left, or divide 6.4 by 10 3 .

0.0074 is the solution.

Working with scientific notation is easier than working with other exponential notation, since the base of the exponent is always 10. This means that the exponents can be treated separately from any other numbers. For instance:

Example 6.3.5

Multiply (2.1 × 10 −7 )(3.7 × 10 5 ).

First, multiply the numbers 2.1 and 3.7, which equals 7.77.

Second, use the product rule of exponents to simplify the expression 10 −7 × 10 5 , which yields 10 −2 .

Combine these terms to yield the solution 7.77 × 10 −2 .

Example 6.3.6

(4.96 × 10 4 ) ÷ (3.1 × 10 −3 )

First, divide: 4.96 ÷ 3.1 = 1.6

Second, subtract the exponents (it is a division): 10 4− −3 = 10 4 + 3 = 10 7

Combine these to yield the solution 1.6 × 10 7 .

For questions 1 to 6, write each number in scientific notation.

For questions 7 to 12, write each number in standard notation.

• 2.56 × 10 2

For questions 13 to 20, simplify each expression and write each answer in scientific notation.

• (7 × 10 −1 )(2 × 10 −3 )
• (2 × 10 −6 )(8.8 × 10 −5 )
• (5.26 × 10 −5 )(3.16 × 10 −2 )
• (5.1 × 10 6 )(9.84 × 10 −1 )
• [latex]\dfrac{(2.6 \times 10^{-2})(6 \times 10^{-2})}{(4.9 \times 10^1)(2.7 \times 10^{-3})}[/latex]
• [latex]\dfrac{(7.4 \times 10^4)(1.7 \times 10^{-4})}{(7.2 \times 10^{-1})(7.32 \times 10^{-1})}[/latex]
• [latex]\dfrac{(5.33 \times 10^{-6})(9.62 \times 10^{-2})}{(5.5 \times 10^{-5})^2}[/latex]
• [latex]\dfrac{(3.2 \times 10^{-3})(5.02 \times 10^0)}{(9.6 \times 10^3)^{-4}}[/latex]

Answer Key 6.3

Intermediate Algebra Copyright © 2020 by Terrance Berg is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License , except where otherwise noted.

Share This Book