in the yeast fermentation experiment what is forming bubbles

An official website of the United States government

Official websites use .gov A .gov website belongs to an official government organization in the United States.

Secure .gov websites use HTTPS A lock ( Lock Locked padlock icon ) or https:// means you've safely connected to the .gov website. Share sensitive information only on official, secure websites.

Publications
Account settings
Advanced Search
Journal List

The bubble-induced population dynamics of fermenting yeasts

Atul srivastava, kenji kikuchi, takuji ishikawa.

Author information
Article notes
Copyright and License information

e-mail: [email protected]

Electronic supplementary material is available online at https://doi.org/10.6084/m9.figshare.c.5194158 .

Received 2020 Sep 10; Accepted 2020 Oct 21; Issue date 2020 Nov.

Bubble-induced transport is a ubiquitous natural and industrial phenomenon. In brewery, such transport occurs due to gas bubbles generated through anaerobic fermentation by yeasts. Two major kinds of fermentation viz. top (ale) and bottom (lager) fermentation, display a difference in their yeast distributions inside a sugar broth. The reason for this difference is believed to be yeast–bubble adhesion arising due to surface hydrophobicity of the yeast cell wall; however, the physical mechanism is still largely a mystery. In this report, through in vivo experiments, we develop a novel theoretical model for yeast distribution based on the general conservation law. This work clarifies that bubble-induced diffusion is the dominant transport mechanism in bottom-fermentation by lagers whereas, yeast–bubble adhesion plays a leading role in transporting ales in top-fermentation, thereby corroborating the centuries-old belief regarding distribution difference in yeast population in two kinds of fermentation.

Keywords: fermentation, adhesion, mixing, modelling

1. Introduction

Bubble-induced transport is a prominent natural phenomenon that occurs across a myriad of biological and industrial settings. In oceans and lakes, gas bubbles produced due to breaking of waves or through generation of methane by blue-green algae act as mixers of nutrients that are vital for functioning of aquatic ecosystems [ 1 ]. On the downside, bubbles carry denser microbes and pathogens to free surface of a water body by adhesion, making local terrestrial fauna including humans susceptible to diseases like influenza and tuberculosis [ 2 ]. This same principle of adhesion that spreads diseases along the shores, is used in industries for wastewater treatment [ 3 , 4 ] and mineral processing to scavenge fine hydrophobic particles through froth floatation. However, a process where bubble-caused transport, involving both mixing and adhesion, significantly stands out is the fermentation by yeasts. At the heart of fermentation lies the yeasts' ability to break glucose molecules down into ethanol and carbon dioxide (CO 2 ) in oxygen-scarce conditions giving off heat, a process that was necessary for yeasts to outlive other microorganisms in an environment that did not yet have oxygen. Besides being possibly the first metabolic pathway [ 5 ], this process of yeast fermentation has been of remarkable value to humanity. It is being exploited since the dawn of agrarian civilizations [ 6 ] to bake bread, make wine and brew beer.

In brewing industry, yeast fermentation is categorized into two broad categories: (a) bottom-fermentation by lager-type yeasts, and (b) top-fermentation by ale-type yeasts [ 7 ]. Lagers tend to occupy lower regions of the fermenting tank and have slower glycolytic kinetics. On the other hand, ales populate upper regions of the tank including the foam (or the bubble layer) at the top and are much vigorous. Since yeast cells are immotile and denser [ 8 ] than the ambient water-based nutrient medium, this difference in population distributions can only arise from CO 2 bubbles they produced during fermentation. Past researchers [ 9 – 11 ] reason that top-fermenting ales have cell walls that are more hydrophobic than their bottom-fermenting counterparts which influences their affinity for bubbles and consequently their population distribution. Also, very recently, Ditscherlein [ 12 ] and Yumiyama [ 13 ] used atomic force microscopy (AFM) to measure interactions between air bubbles and immobilized yeast cells to estimate adhesion force between them. Though it has been recognized that hydrophobicity-based yeast–bubble adhesion [ 14 ] can be a key player in yeast distribution difference in two kinds of fermentation, adhesion yeast transport is still an unproven hypothesis. It is also important to mention here that, to the best of our knowledge, a bubble that carries yeast cells by adhesion inside a fermenting tank has never been directly observed.

Bubbles also act as natural mixers. When they rise after their formation, they disturb the surrounding fluid and create background velocity fields that cause yeasts in the fermenting tank to move passively with the flow. These velocity fields and their mixing strengths have been extensively investigated in the past to optimize the fermentation process and design fermenting vessels that avoid nutrient gradients [ 15 – 19 ]. Zhang et al . have highlighted the significance of such mixing phenomenon in large-scale fermenters of starch by estimating the liquid circulation rate and modelling the effects of bubbles using its average rise velocity and flow fields around it [ 20 ]. Schmidt & Velten [ 21 ] numerically simulated these bubbly flows and used it to estimate average nutrient homogenization times during different stages of fermentation by using diffusion of a passive tracer as an indicator of such mixing phenomenon. As far as effects of bubble-induced velocity fields on yeast population is concerned, a few experimental studies have reported gradients in yeast concentration profiles in unstirred fermenters in regimes of low bubble production [ 22 – 25 ]. Also, Klembt & Meironke [ 26 ] have recently modelled natural convection for bottom-fermentation and used it to investigate yeast distribution inside a conical fermentation tank. Markedly, all these former researches have approached the problem of bubble mixing and yeast distribution in fermenters independently of yeast–bubble adhesion.

In this study, based on novel experiments and in vivo visualization techniques, we categorically probed all major mechanisms of yeast transport, namely, (a) bubble-induced mixing of cells, (b) ascension of cells by adhesion to bubbles and (c) cell sedimentation. As discussed, even though past researchers in the field have reported the presence and significance of these mechanisms, none of them clarified the contributions of these mechanisms towards yeast distribution in fermenting tanks. This is primarily because we do not have a unified theoretical model for yeast transport. In the present work, we propose a governing equation for yeast population distribution, which enables us to quantitatively understand the relative importance of each of the aforementioned mechanisms. This is achieved by extracting constituent yeast fluxes from total yeast flux through a mathematical model. We go on to show that yeast's strategy of adhering to self-generated bubbles is the more dominant of the two bubble-caused mechanisms in the case of top-fermentation by ales, whereas bubble-induced mixing plays a dominant role in bottom-fermentation by lagers. This study confirms for the first time the long-standing speculation of yeast–bubble adhesion, which leads to differences in yeast distribution in the two kinds of fermentation.

In the next section, we present our experimental results on yeast population dynamics in fermentation including our observations regarding the three yeast transport mechanisms. In §3, we propose a mathematical model for yeast transport that rests upon the general conservation law. Section 4 discusses how transport phenomena in top-fermenting ales differs from that of bottom-fermenting lagers. Finally, in §5, we present our concluding remarks. The details of our experimental and computational techniques can be found in §6.

2. Experimental results

2.1. yeast population dynamics.

Our archetypal fermenting flask with a rectangular cross-section area was filled with 50 ml of standard YPD nutrient broth. The flask was inoculated near the floor with freshly cultured yeasts ( S. cerevisiae ), and activity inside it was observed over 3 days. From figure 1 , based on bubble production, the bustle is classified into three phases. The phases 1, 2 and 3 for ale yeasts, respectively, occur during t = 0−20 h, t = 20− 60 h and t > 60 h post-inoculation, whereas for lager yeasts they last between t = 0−30 h, t = 30−70 h and t > 70 h, respectively. We elucidate these phases in subheads to follow.

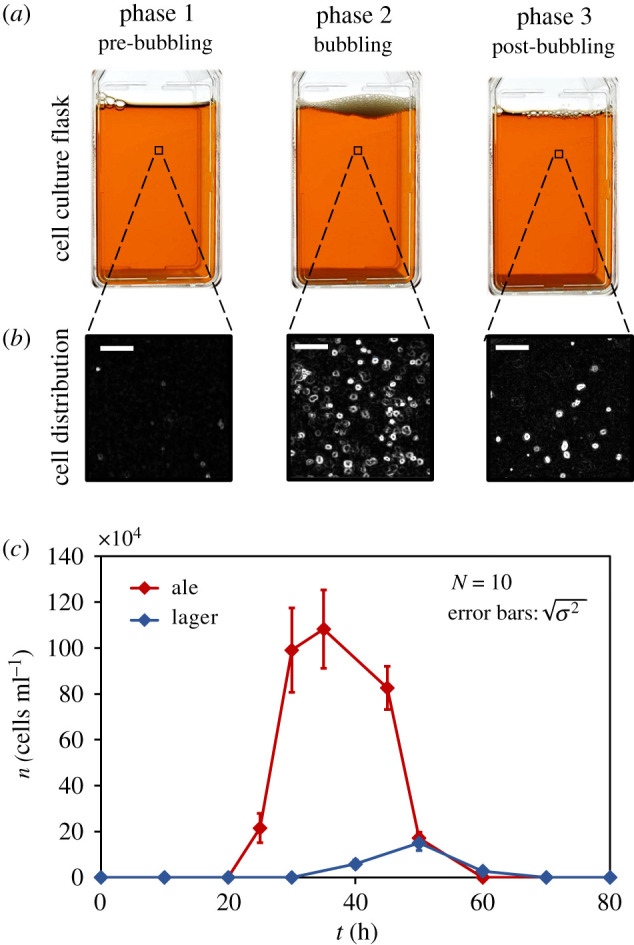
Yeast activity in YPD broth: ( a ) images of cell culture flask in three different phases based on bubble production for top-fermenting ales. ( b ) Magnified images showing yeast cells in the fluid medium in three different phases. Scales are 100 µm. ( c ) Variation in yeast population n in lower regions of the fluid medium for ale and lager yeasts. Error bars denote s.d. ( N = 10).

2.1.1. Pre-bubbling

Apparently quiescent, the pre-bubbling phase is free from any suspended yeasts in the fluid medium. However, inoculated yeasts at the flask floor metabolize sugar by anaerobic fermentation to produce ATP and grow. CO 2 released as a by-product dissolves in the ambient fluid. Within 20 h of inoculation (for ales), the yeast population at the floor becomes very high (approx. 10 11 cells ml −1 ) and a rough hydrophobic layer of yeast cells is formed. Also, by this time, cells begin the diauxic shift in their metabolism due to sugar limitation [ 27 – 29 ]. Note, there is no transport of yeasts from the floor upwards into the fluid medium during this phase, but it creates conditions that are ripe for yeast transport in the next phase. The formation of yeast cell layer and dissolution of CO 2 in the medium encourages generation of bubbles.

2.1.2. Bubbling

When fluid saturates with CO 2 , the presence of hydrophobic crevices in yeast cell layer lead to heterogenous nucleation of gas bubbles [ 30 ] as displayed in figure 2 a . These bubbles accrete dissolved CO 2 from their ambience and when the buoyant force on them becomes large enough, they detach from cavities and ascend upwards to collectively create a bubble layer (foam) at the top. This rise of gas bubbles induces yeast transport that leads to a non-zero cell distribution above the floor which can be seen in figure 1 . We measured bubble flux f ( t ), which is the frequency of bubbles generated at the flask floor per unit area, with time and superimposed it on the suspended cell population to get figure 2 b . It can be noted that time periods of zero bubble flux closely correspond with time periods of zero suspended cell population. Eventually, as bubbling dies out, the process enters into the post-bubbling phase.

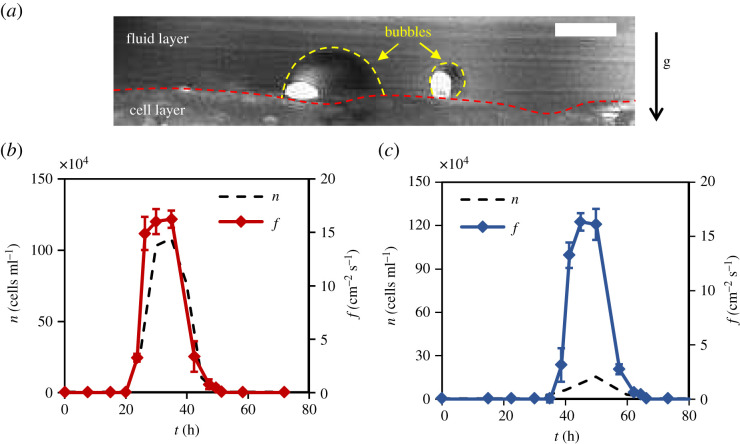
Bubble generation: ( a ) an illustration of gas bubble formation at the bottom of the fermenting flask. Broken yellow lines mark the edge of the bubbles and the broken red line marks the boundary of the cell layer. The scale is 300 µm. ( b , c ) An overlapping representation of bubble flux f and yeast population n for ales ( b ) and lagers ( c ). Error bars represent s.d. ( N = 5).

2.1.3. Post-bubbling

When the bubbling stops, yeasts have no reason to remain suspended. Owing to their greater density than that of the ambient fluid, sedimentation takes over and yeasts gradually return to the floor.

This three-phase, 3-day long phenomenon of yeast population dynamics is explored in sections to follow, where we investigate how such transport of immotile yeasts occurs inside a fermenting flask.

2.2. Bubble-induced mixing

One of the transport mechanisms is natural agitation in the medium created due to ascending gas bubbles. In addition to displacing fluid by virtue of its motion, bubbles form an upward fluid drift along its axis of ascent [ 31 – 33 ] as illustrated in figure 3 a . Electronic supplementary material, movie shows the particle image velocimetry (PIV) of these flow fields in an observation window. When plenty of such bubbles sweep through the fluid regime, we get what is called a pseudo-turbulence [ 34 ]. It occurs at relatively small Reynolds numbers ( Re ); however, the levels of liquid fluctuations are comparable to fully turbulent flows [ 35 ]. For Re ≤ 50, the intensity of bubble-induced velocity fluctuations are determined by the micro-structures formed due to bubble spatial distribution [ 36 ], whereas at large Re ≥ 200, it is influenced by wake interactions [ 32 ]. Such pseudo-turbulence leads to a mixing in the fermenting tank, which is usually modelled as a Fick's diffusion phenomenon. In the current fermentation setting, where the bubbling is non-homogeneous in space, we have two scales of mixing: (a) small-scale mixing arising due to bubble rise in the fluid regime, called bubble-induced turbulence (B.I.T.), and (b) large-scale mixing coming from fluid velocity gradients due to non-uniform distribution of bubbling source points at the flask floor, called shear-induced turbulence (S.I.T.) [ 37 , 38 ].

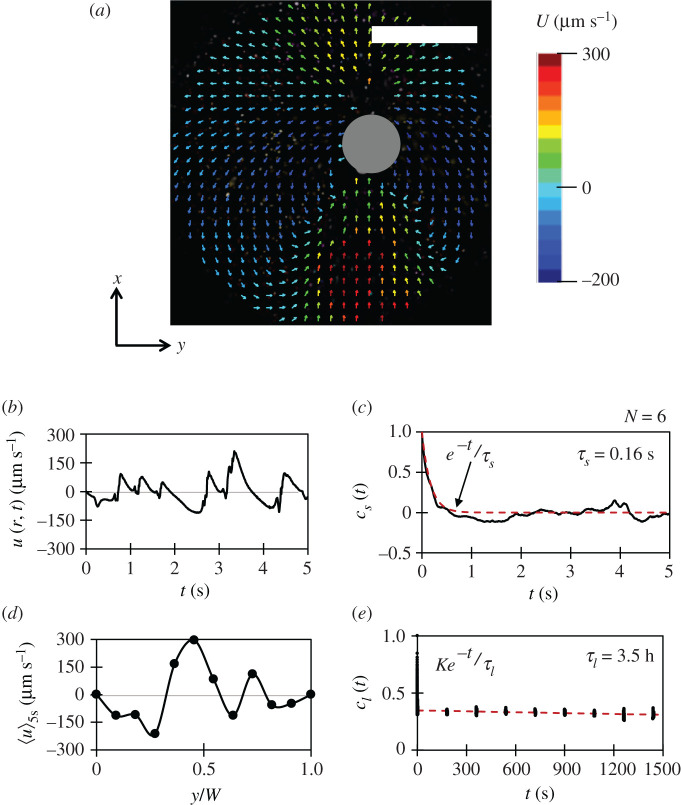
Bubble-induced mixing: ( a ) the instantaneous vertical fluid velocity vectors around a rising gas bubble (grey circle) at middle of the flask. Here, y is the horizontal (radial) direction and x is the vertical (axial) direction. The scale is 1 mm. ( b ) The time record of vertical fluid velocity fluctuations u ( r , t ) at some location r in the circular observation window C of radius 3 mm. ( c ) The time correlation c s ( t ) for the vertical velocity fluctuations to estimate small-scale diffusivity. ( d ) The vertical velocity profile along the width W of the flask. Note, when averaged over the width W , it is zero. ( e ) The time correlation c l ( t ) to estimate the deformation timescale for the illustrated velocity profile.

In this paper, since we are primarily interested in 1-D yeast population dynamics in the vertical direction, we performed a series of experiments to estimate the vertical diffusivity (or axial dispersion) averaged horizontally, for both, small-scale mixing and large-scale mixing.

For small-scale mixing, we focused at various locations on the middle of the flask along the width and observed the time variation in vertical fluid velocity fluctuations u ( r , t ) at various position r , such that

where U ( r , t ) is the vertical fluid velocity component and 〈 U ( r , t )〉 5s is the averaged vertical fluid velocity for 5 s. These fluctuations had a mean correlation time τ s = 0.16 s with the mean standard deviation u s = 65.2 µm s −1 ( figure 3 b,c ). Using these, the small-scale vertical diffusivity can be scaled as D s ∼ u s 2 τ s = 6.8 × 10 − 6 c m 2 s − 1 . However, this estimation is incomplete when compared with the experimental results (see electronic supplementary material, document (S6)). It is because the diffusivity D s does not incorporate the mixing effects due to large-scale fluid recirculation [ 39 ].

Moving on, to scale the large-scale mixing, firstly, we measured the variation in averaged vertical fluid velocity 〈 U 〉 5s , along the horizontal direction y ( figure 3 d ). It can be seen that the vertical velocity profile is non-uniform along the width due to non-uniform distribution of bubble source points, which causes large recirculation in the fermenting flask. Note, when 〈 U 〉 5s is averaged through the entire flask width W , we get 〈〈 U 〉 5s 〉 W ≈ 0. The 1-D recirculation velocity scale for the flask, however, can be extracted as u l = ⟨ ⟨ U ⟩ 5 s 2 ⟩ W = 136.6 μ m s − 1 .

Now, to obtain the timescale for large-scale mixing, we estimated the time it takes for the illustrated velocity profile ( figure 3 d ) to deform. It was done by observing the variation in U at six different locations along the width for 60 min through 5 s long PIV measurements that were 3 min apart and then obtaining its mean time correlation ( figure 3 e ). It turns out that the correlation for vertical velocity profile decays slowly, with a time constant of τ l = 3.5 h, yielding a diffusivity scale D l ∼ u l 2 τ l = 2.35 c m 2 s − 1 . Note that the corresponding length scale can be obtained as L l ∼ u l τ l = 1.71 m , which is much greater than the dimensions of the flask. So, since the large-scale vertical diffusivity is limited by the height of fluid regime, a better scaling argument for it can be D L ∼ u l H = 8.2 × 10 − 2 c m 2 s − 1 , where H is the height of fluid regime. More details on the merits of using such scaling can be found in electronic supplementary material, document (S7). Finally, the total vertical diffusivity inside a fermenting flask, including both small and large-scale mixing, can be given as D = D s + D L ≈ 8.2 × 10 −2 cm 2 s −1 , which is about eight orders of magnitude higher than the Brownian diffusivity (approx. 4.39 × 10 −10 cm 2 s −1 ) of yeasts.

As an aside, since the strength of small-scale mixing is influenced by the size, speed and gas volume fraction of the bubbles, we would like to report them here from our experiments. The bubble Reynolds number is O (10) with mean bubble diameter d = 306.8 ± 29.1 µm and mean bubble velocity U B = 4.1 ± 0.5 cm s −1 . This measurement of U B is much closer to the Stokes prediction (approx. 5 cm s −1 ) of terminal rise velocity rather than the Hadamard–Rybyczynski prediction (approx. 7 cm s −1 ) due to the presence of trace surfactants and non-cleanliness of the medium [ 40 ]. Also, note, a variation in bubble size and rise velocity is not observed with height in our experiments because the change in pressure along height is negligible, the bubble terminal velocity is achieved within tens of milliseconds, and the volume fraction α = f ( t ) V ∗ / U B at bubbling peak is O (10 −4 ), where V * is the mean bubble volume.

2.3. Yeast–bubble adhesion

Another mechanism of yeast transport is through yeast–bubble adhesion. As mentioned earlier, ale yeasts are highly hydrophobic in nature. This property arises from the presence of surface proteins on their cell walls which encourages them to adhere to a bubble surface, effectively turning bubbles into yeast vehicles. In our experiments, using a horizontal microscope and a high-speed camera, we observed rising gas bubbles carrying yeast cells ( figure 4 a ), which is, possibly, the first direct evidence of adhesion transport inside a fermenting tank. Furthermore, during the peak of bubbling, when we zoomed in on the bubble layer–fluid medium interface ( figure 4 b ) we noted yeast groups clinging to interfacial gas bubbles. These observations of yeast–bubble adhesion are very different from the reports of Walls & Bird [ 41 ].

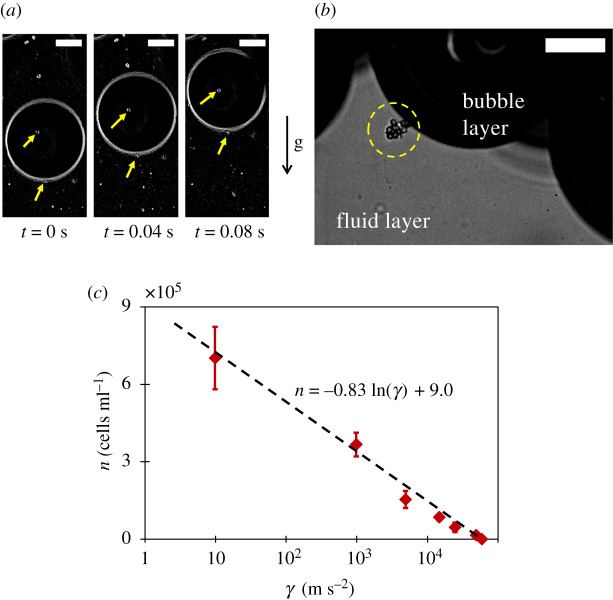
Yeast-bubble adhesion : ( a ) a gas bubble carrying top fermenting ale yeasts. Scales are 100 µm. ( b ) An illustration of yeast–bubble adhesion (yellow circle) during fermentation at the bubble layer–fluid medium interface. The scale is 100 µm. ( b ) The measurement of bubble layer–fluid medium interface yeast population n with increasing magnitudes of centrifuging acceleration γ in order to estimate the adhesion force F a between yeasts and a bubble. Black broken trendline has R 2 = 0.99. Error bars denote s.d. ( N = 5).

As the next step, we attempted to measure the adhesion force between yeast and bubbles by subjecting the bubble layer–fluid medium interface to increasing magnitudes of centrifuging acceleration and subsequently measuring the interface yeast population ( figure 4 c ). The threshold acceleration γ at which this population became zero (meaning, all yeast cells are separated from interfacial bubbles), was used to estimate the adhesion force as F a = γ V y Δ ρ , where V y (2.48 × 10 −16 m 3 ) is the volume of a yeast cell and Δ ρ (72 kg m −3 ) is the density offset (estimated in the next section) between yeast and the ambient fluid. The experiments yielded an average adhesion force F a = 1.02 nN.

2.4. Sedimentation

We now turn to a transport mechanism that is not bubble-induced, but is present due to greater density of yeasts than its ambience. To begin, we estimated the average density ( ρ y ) of a yeast cell in the medium by using Stokes' drag law for a smooth rigid sphere (here, yeasts) falling in a viscous fluid as ρ y = ρ m + 9 μ U o / 2 g a 2 , where ρ m is the density of the medium, a and V are the radius and volume of a yeast cell, μ is the viscosity of the medium, U o is the terminal speed of yeast sedimentation and g is the acceleration due to Earth's gravity. We considered yeasts to be approximately spherical with average radius a = 3.9 ± 0.7 µm and measured yeast sedimentation speed in YPD medium ( figure 5 a ) as U o = δ x / δ t , where δx is the sedimented distance in δt time. Note, this experiment was done just after yeast inoculation ( t = 0) i.e. before the onset of multiplication and in pre-bubbling phase to ensure, observation of single yeast cells without buds (so that they can be considered spheres) and to eliminate bubble-induced effects. The measured value of average yeast sedimentation speed was U o = 2.50 ± 0.76 µm s −1 . By assuming the viscosity of YPD medium to be 0.001 Pa s, the average yeast density ρ y was calculated to be 1072 kg m −3 .

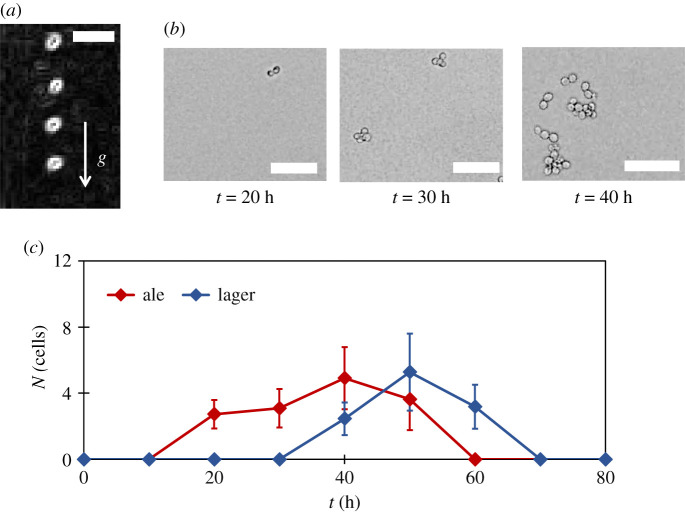
Yeast sedimentation: ( a ) an example of single ale yeast sedimentation. The overlapped images are 4 s apart and the images are edge enhanced. The scale is 10 µm . ( b ) An illustration of typical ale yeast groups in the fluid medium at different times. Scales are 50 µm. ( c ) The time variation of average number of yeasts N in a group inside the medium due to flocculation and cell division for ale and lager yeasts. Error bars denote s.d. ( N = 10).

Apparently, with values of U o and ρ y , we have all the information about yeast sedimentation. However, yeasts display a special nuance that makes the phenomenon of sedimentation a little more complex. Yeast have a capacity to form groups in nutrient broths that are manifested either as chains or flocs. The chains are formed due to yeast growth where a mother cell forms daughter cells, which in turn forms new buds. Theoretically, these chains can grow indefinitely given the availability of nutrients, but they are broken down through shear forces in the suspension which limits their sizes to approximately 3–4 cells per group. Also, flocculation [ 42 ] is another important process through which yeasts form clusters as fermentation proceeds through mechanisms that are not entirely clear yet. These groups are bigger and are called ‘flocs' with their sizes ranging from approximately 5–60 cells per floc. Sample suspended yeast groups at different time instants are shown in figure 5 b . Also, more elaborately, such increase in the average size of a yeast group (by number of cells) is measured to obtain figure 5 c . It can been seen that the average number of yeasts ( N ) in a suspended yeast group varies with time. This phenomenon of group formation influences yeast sedimentation velocity which we will address during modelling.

3. The yeast transport model

3.1. problem setting and the governing equation.

Having investigated the roles that bubbles play in transporting yeasts during fermentation along with yeast sedimentation, we now develop a unified yeast transport model and employ it to understand the comparative significance of these mechanisms in two kinds of fermentation. Our problem setting is schematically shown along with three modes of yeast transport in figure 6 . The fermenting flask has a yeast cell layer at the bottom, the fluid medium of height h in between and a bubble layer of thickness b at the top. The yeast flux, both in the fluid medium and in the bubble layer, has an advection–diffusion form of

where n is the number density of yeasts averaged over the horizontal cross-section, x ^ is the unit vector pointing vertically upwards, J a = | J a | x ^ is the vertical flux due to yeast–bubble adhesion, V is the advection yeast velocity due to fluid fluctuations, U s is the yeast sedimentation velocity and D is the bubble-induced diffusivity.

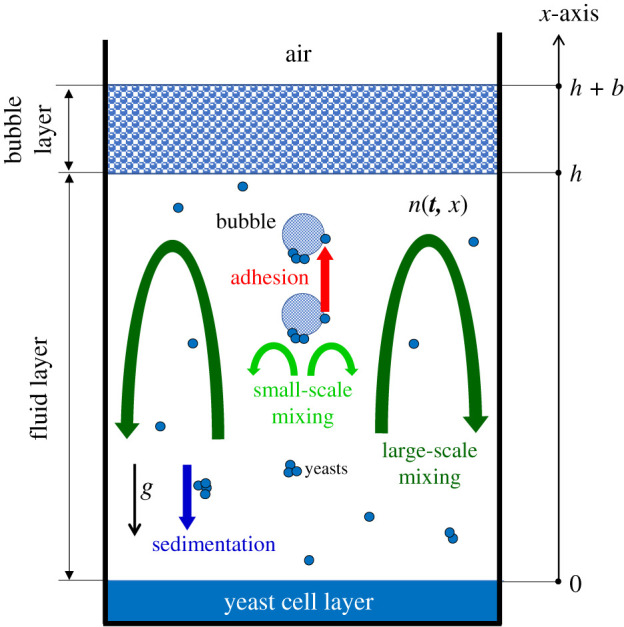
A schematic of analytical setting of yeast transport phenomena in nutrient broth, where n ( t , x ) is the time-varying one-dimensional distribution of yeasts in the fluid medium and in the bubble layer. The x -axis originates from the surface of the yeast cell layer and is directed vertically upward.

On applying the equation of continuity to equation (3.1), we get

where α is the yeast growth rate.

Furthermore, integrating equation (3.2) over the horizontal cross-section of the flask, and simplifying gives us

Now, since the convection flow (mixing) generated by bubbles and yeasts satisfy conservation of mass, the advection velocity V averaged over the horizontal cross section is zero. Therefore, fluid velocity fluctuations do not contribute to the advection term, though they cause diffusion. So, finally, the governing equation for yeast population distribution along vertical direction x becomes,

In the next few subheads, we will model the terms in equation (3.4), firstly inside the fluid medium and then in bubble layer.

3.2. Diffusion flux

In §2.2, we estimated the more dominant of the two vertical diffusivities in the fluid medium at the peak of bubbling as D L ∼ u l H , where symbols have the usual meaning. When fewer bubbles are produced as bubble flux departs from its maximum, the mixing strength is weaker due to smaller magnitudes of flow velocity vectors. This dependence of vertical velocity scale u l on bubble production may be considered proportional to bubble flux as u l ∝ f ( t ), given that the velocity disturbances are generated discretely in time (cf. figure 3 b ) and its time average is roughly the summation of such discrete events. Considering this, the dynamism of vertical diffusivity can be modelled like, D ( t ) = D L f ( t ) / f p , where f p is the maximum value of f ( t ) for top-fermenting yeasts. The same equation can be used to represent bubble mixing for bottom-fermenting yeasts, but with a different f ( t ). It should be noted, though we are calling this the ‘bubble-induced diffusivity', it contains effects of other small-scale diffusive phenomena such as, Brownian motion and thermal effects, that occur simultaneously within the flask, because our experiments are done in situ .

Yeast diffusion inside the bubble layer also occurs due to bubble flux f ( t ) generated at the flask floor. In the bubble layer, upward advection happens due to the arrival of new bubbles at its bottom and breaking up of old bubbles at the top. If averaged over horizontal cross section, this behavior mimics a queue (assuming it to be of constant thickness in this timescale) causing a net upward movement of yeasts. The upward velocity depends upon the bubble volume and the bubble flux. We scale such advection velocity as U b ∼ V ∗ f ( t ) where V * is the average volume of a bubble. For length scale, bubbles travel a vertical distance of b in the bubble layer, and yeast ascend or descend depending on the bubble generated flow which also has a length scale of b . Thus, the thickness of the bubble layer in the flask can be a good estimate of this length scale. Considering these, the vertical diffusivity in the bubble layer D b can be scaled as D b ∼ V ∗ f ( t ) b .

3.3. Adhesion flux

The second kind of yeast flux is from yeast–bubble adhesion. Assuming each bubble carries c cells from cell layer to the bubble layer, the adhesion flux in the fluid medium can be modelled as J a ( t ) = c f ( t ) x ^ , where f ( t ) is the measured bubble flux. Now, in order to estimate c , we measured the average number of top-fermenting ale yeasts c b adhered to a bubble near the bottom of the bubble layer. Experiments yielded a value of c b = 16.7 ± 3.47. However, we found that this value did not correspond to actual c , because some yeasts fall down from the bubble layer due to gravity. Only measuring c b , therefore, is not good enough. Since, the value of c is difficult to estimate directly through experiments, we obtained it through least square fitting to the experimental part of data shown in figure 8 a . The fitting showed that each bubble carries on an average 32 top-fermenting yeast cells from cell layer to bubble layer by adhesion (i.e. c = 32). Our confidence in this estimation was achieved when the numerical simulation with c = 32 showed c b = 17.8, which falls within the standard deviation of experimental measurement of c b .

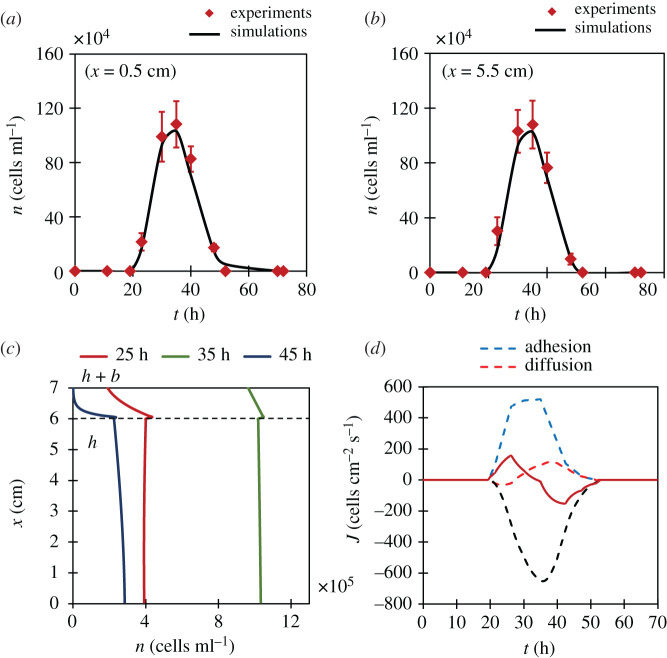
Top-fermenting ales: the comparison between simulation and experiments at lower ( a ) and upper ( b ) regions of fluid medium. Error bars denote s.d. ( N = 10). ( c ) The representation of population gradient with height at different time instants in fermentation. Note the positive gradient at 25 h. ( d ) Splitting of overall yeast flux through middle of the flask into its constituent fluxes. Note the dominance of adhesion flux over diffusion flux.

In bubble layer, the adhesion flux is given by J a ( t ) = U b n x ^ , where U b is the upward advection velocity in the bubble layer which can be scaled as U b ∼ V ∗ f ( t ) . In the case of bottom-fermentation, we did not observe any yeast–bubble adhesion. Hence, we simply assume c = 0.

3.4. Sedimentation flux

In §2.4, we showed that the size of a suspended yeast group is time-dependent. The number of yeasts ( N ) in a suspended yeast group has an important implication on its sedimentation velocity. By assuming that the yeast group has roughly a spherical configuration, a variation in N as N ( t ) brings about a corresponding variation in equivalent spherical radius of the group as a g (t) = aN ( t ) 1/3 , where a is the radius of a yeast cell. Viscous drag in Stokes flow increases proportional to the radius, while sedimentation force increases proportional to N . Therefore, the sedimentation velocity, by Stokes drag law, follows the equation, U s ( t ) = U ( t ) = U o N ( t ) 2/3 , where U o is the sedimentation velocity of single yeast cell measured in §2.4. The yeast flux arising due to such yeast sedimentation in fluid regime can ultimately be expressed as − U s ( t ) n x ^ , where negative sign indicates a vertically downward movement.

In bubble layer, the drag on yeast cells is reduced as the bubble film is thin, which has an effect to increase its vertical sedimentation velocity. Drag reduction of a particle in a two-dimensional fluid film was first analysed by Saffman & Delbruck [ 43 ]. Cheung et al . experimentally confirmed Saffman's calculation and found that the drag on a hard sphere in free-standing soap film was reduced [ 44 ] approximately by a factor of one-third. It should be noted that the path traced by yeasts inside the bubble layer is not a straight line rather, yeasts follow the curvatures of the bubbles. This trajectory effectively decreases the vertical sedimentation velocity of yeasts in the bubble layer. Since the two phenomena (namely, film thickness and bubble curvature) have opposite effects, we reasoned that the sedimentation velocity in the bubble layer is of a similar order to that in the fluid medium, i.e. U b = U s ( t ).

Lastly, we assumed that such yeast sedimentation velocity is independent of the fluctuating liquid velocity because the size of a yeast cell is about 10 µm, which is considerably smaller than the bubble diameter of 306.8 µm. Hence, the flow field around a yeast cell can be approximated as linear and expressed simply by the rate of strain tensor. Moreover, the Reynolds number of a sedimenting yeast is much less than unity, and the flow can be approximated as Stokesian. In the case of linear Stokes flow, we can superimpose velocities generated by different physical origin. Therefore, we assumed that the sedimentation velocity can be superimposed to other velocities caused by diffusion and adhesion.

3.5. Yeast growth

Another important contributor to yeast population (cf. equation (3.4)) is yeast growth rate α . The doubling time for ale and lager yeasts before the pre-bubbling phase in our experiments is 90 min, which lasts for about a 20 h post-inoculation for ales and 40 h for lagers. In the bubbling phase, we assume that yeasts have undergone a diauxic shift towards aerobic metabolism of ethanol during which the yeast growth was negligible as compared to during anaerobic glycolysis [ 27 , 28 ]. Finally, in the post-bubbling phase, yeasts were apparently in the stationary phase of zero growth. So, we modelled the yeast growth rate α = 0.007[ H ( t ) − H ( t − t o )] min −1 , where H ( t ) is the Heaviside step function and t o = 20 h for ales (40 h for lagers). Also, in bubble layer, we assumed α = 0, due to the absence of nutrients.

3.6. Boundary conditions

After defining and modelling all constituent terms in equation (3.4), the complete description of our problem requires knowledge of physical phenomena going on at boundaries. The problem has three boundaries: a cell layer–fluid medium interface at bottom of the fluid regime ( x = 0), a bubble layer–fluid medium interface ( x = h ) and a bubble layer–air interface at top of the bubble layer ( x = h + b ).

3.6.1. Cell layer–fluid medium interface

This boundary supplies yeast cells to the fluid regime with the help of bubbles from cell layer. At the interface, we observed a clear discontinuity in yeast concentration with 10 11 cells ml −1 in cell layer whereas about a maximum of 10 6 cells ml −1 for ales and 10 5 cells ml −1 for lagers in the fluid medium. The discontinuity is kept by cell–cell binding that stems from hydrophobicity, surface charges and zymolectin interactions [ 45 ] which leaves only loosely bounded yeasts to lifted by bubbles wake or adhesion. Since diffusion flux cannot express such a discontinuity, we neglected it at the interface. Instead, we introduced an ascending flux caused by bubble's wake, on top of the one caused by adhesion of yeast to a bubble, because a bubble ejected from a crevice pulls up some surrounding cells to the fluid medium without adhesion. We assume that the bubble's wake flux is proportional to bubble flux as c ′ f ( t ) x ^ , where c ′ is the number of yeasts brought into the medium through each bubble's wake. To estimate the value of c ′, we measured yeast distribution near the lower portion of the flask for bottom-fermenting yeast, and since lagers do not adhere to bubbles (i.e. c = 0), the yeast supply is primarily due to the bubble's wake. The least square fitting of simulated solution to measured distribution yielded the optimal value of c ′ as 4.5. The fitting data can be found in electronic supplementary material, document (S2). Eventually, flux at the bottom boundary can be written as J ( t , 0) = ( c + c ′) f ( t ) − U s n | x →+0 , where n | x →+0 indicates n in the fluid medium just above the interface.

3.6.2. Bubble layer–fluid interface

With knowledge of yeast transport both in the bubble layer and in the fluid medium, flux exchange at this interface is expressed as J ( t , h ) = c f − U s n | x → + h − D R ( ∂ n / ∂ x ) , where U s n | x →+ h is defined at the bottom of the bubble layer just above the interface and D R is the resultant diffusivity across this interface. The resultant diffusivity stems due to a difference in magnitudes of bubble-induced diffusivities in bubble layer and fluid medium (for derivation of D R , see electronic supplementary material, document (S4)).

3.6.3. Bubble layer–air interface

Finally, since yeasts cannot fly into the air, the boundary condition at top of the bubble layer is simple. There is no flux exchange and hence, J ( t , h + b ) = 0.

4. Discussion

The proposed governing equation for yeast transport (equation (3.4)) with boundary conditions discussed in the previous section was solved using the standard finite volume method (FVM). We will now discuss how this mathematical model can explain yeast population dynamics for bottom-fermenting lagers and top-fermenting ales.

4.1. Bottom fermentation

Figure 7 a , b shows the comparison of simulation results with yeast distributions near upper and lower regions of the fluid medium. Since, the adhesion yeast supply c from cell layer is zero for bottom-fermenting lagers, this distribution is generated solely due to bubbles' wake yeast supply c ′. The agreement between yeast distributions, in both the graphs, confirms this claim. This means for bottom-fermenting yeasts, superior bubble-induced transport mechanism is bubble-induced diffusion due to non-existence of adhesion yeast flux. Figure 7 c shows numerical results of yeast distribution along the height of the flask. Note that this gradient is always negative implying the yeast population at lower regions in the fluid is always greater than at upper regions which is intuitive. Even during the peak of fermentation (i.e. 55 h) such gradients are appreciable. Such inhomogeneities in yeast population may affect fermentation kinetics and process control [ 23 ]. Finally, to understand the relative strengths of each transport mechanism, using our model, we separated ( figure 7 d ) the total yeast flux into its constituent parts. In the initial stages, upward diffusion flux dominates sedimentation giving rise to a net upward flux. However, during the fag end of the fermentation, sedimentation takes over to bring yeasts back to the cell layer.

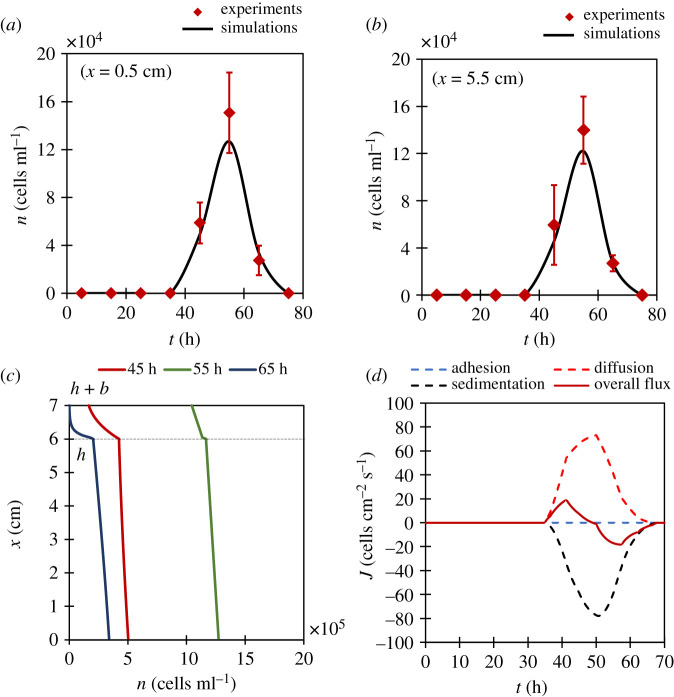
Bottom-fermenting lagers: the comparison between simulation and experiments at lower ( a ) and upper ( b ) regions of fluid medium. Error bars denote s.d. ( N = 5). ( c ) The representation of population gradient with height at different time instants in fermentation. Note the gradients are predominantly negative. ( d ) Splitting of overall yeast flux through middle of the flask into its constituent fluxes. Note the absence of adhesion flux.

4.2. Top fermentation

We did the same analysis for top-fermenting ales. Figure 8 a , b validates our model with experiments. It should be noted that the peak yeast population for top-fermenting ales in the fluid medium is 1.1 × 10 6 cells ml −1 which is about seven times as compared to that of bottom-fermenting lagers. In top-fermentation, these excess yeasts are supplied by adhesion, thus establishing adhesion as the dominant mechanism of yeast transport for ales. In figure 8 c , we show numerical results of yeast distribution with height at different times. A slight positive gradient in the fluid medium at 25 h implies that the yeast population in the upper regions of the fluid exceeds the population in lower regions. This means that during this stage more yeasts reached the bubble layer and sedimented (and diffused) downwards into upper regions of the fluid medium, which can only be achieved if we have an adhesion flux. The negative gradient at 45 h signifies the obvious dominance of sedimentation over other two mechanisms. For the rest of the time, when bubble production is high, concentration in the fluid medium is fairly homogeneous. Lastly, figure 8 d separates the total yeast flux into its constituent parts based on the proposed mathematical model. The dominance of adhesion flux is clearly seen in initial stages of fermentation.

5. Conclusion

In this work, we started from the observation of yeast population dynamics in an unstirred fermenting flask for top-fermenting ales and bottom-fermenting lagers, and then delved deeper to probe yeast transport mechanisms through in vivo visualization techniques. We noted that there are three major mechanisms of yeast transport out of which two are bubble-induced viz. adhesion and mixing. The third mechanism is dynamic yeast sedimentation arising due to flocculation. A superposition of these mechanisms gave rise to observed population dynamics inside the flask, which was confirmed through a theoretical model based on general conservation law. This is the first mathematical model of its kind that links yeast concentration distribution during fermentation to its transport mechanisms. Our simulation results showed that the dominant mechanism in the case of bottom-fermenting lagers is diffusion since the yeast supply from cell layer due to adhesion is missing, whereas in the case of top-fermenting ales, adhesion was confirmed as the dominant mechanism of transport.

This report has established the centuries-old belief in brewing industry that differences in yeast distributions in top-fermentation and bottom-fermentation come from yeast–bubble adhesion. The strategy of yeasts to adhere to a bubble is much effective when compared with any other microbial transport phenomena, as it facilitates an immotile, denser cell to migrate a long distance with speeds of the order of centimetres per second (bubble rise velocity) without any mechanical work. Our mathematical approach can be extended to large scales, to water bodies (for example, methane fermentation by bacteria [ 46 ] in lakes and bubble-induced nutrient mixing in ocean [ 1 ]) and to brewing industries. Further, we can generalize our study, through a simple test, to make falsifiable predictions as to whether an unknown yeast strain is a bottom or top fermenter. The test involves homogeneously inoculating a strain of yeast into a nutrient broth and allowing it to sit for about 6 h to allow complete cell sedimentation and then observing the fluid–air interface. If there are many cells adhering to the interface at this point in time, the strain is expected to behave as a top-fermenter when bubbling commences (see electronic supplementary material, document (S5)).

6. Material and methods

6.1. cell culture protocol.

For our experiments, we used highly flocculent strains of S. cerevisiae of top-fermenting (Fermentis, SAFALE S-04) and bottom-fermenting (Fermentis, SAFLAGER S-24) types. The yeast culture was performed as a three-step process involving dry yeast hydration, a solid YPDA (Yeast Extract, Peptone, d -glucose, Agar) culture and a liquid YPD culture. The cells obtained after this process were called ‘freshly cultured yeasts' and were used in all investigations. Our cell culture protocol in more detail can be found in electronic supplementary material, document (S1).

6.2. Yeast population distribution measurement [ n ( t )]

We inoculate 100 µl of freshly cultured yeasts, near the flask floor, in 50 ml YPD broth (approx. 10 3 kg m −3 ) inside a cell culture flask (tissue culture flask 50 ml, FALCON), such that the initial yeast concentration inside the flask is approximately 10 4 cells ml −1 throughout. This flask has a rectangular cross-sectional area of 8.33 cm 2 and the height of fluid level inside the flask is 6 cm. After the inoculation, the flask is left unstirred at room temperature (24°C) with light condition of about a 100 lux. The yeast population near the top (at 5.5 cm) and bottom (at 0.5 cm) of this flask were then measured at different time instants over 3 days by taking out aliquots of 10 µl and observing it under a vertical microscope (CX-10C, OL-140, HiROX).

6.3. In vivo visualization technique

Our experimental techniques for observing suspended yeasts in figure 1 , bubble nucleation in figure 2 a , illustration of adhesion in figure 4 a and estimation of sedimentation velocity in figure 5 a , all used the same visualization set-up. The fermenting flask was back illuminated with a white light source which is an optical fibre and was observed horizontally with the help of horizontal microscope fitted to a high-speed camera (Phantom v. 7.1, Vision Research).

6.4. Bubble flux [ f ( t )]

It was measured with the help of a DLSR camera (D5200, NIKKOR 18–55 mm, Nikon) focusing on the cell layer and counting manually the number of bubbling points and the number of bubbles generated by them per second. This was done for entire floor area to get the bubble flux as f ( t )/cm 2 s.

6.5. Particle image velocimetry measurements

For PIV measurements, a cell culture flask containing 50 ml of YPD broth was inoculated with 10 4 freshly cultured yeasts per ml. Thirty-five hours (peak of fermentation) after the inoculation, a vertical plane within the flask was illuminated from the sides with red sheet lasers (670 nm) inside a chamber. The flask was then observed with the help of a high-speed camera and a horizontal microscope in a 3 mm observation window. Velocity vectors for flow fields were obtained using 2D-PIV (Flownizer2D, DITECT) by measuring the cross-correlation between successive frames in a movie [ 47 ]. Note that there was no need to seed the suspension with tracer beads, as yeast cells scattered enough light for flow visualization. The sampling frequency for the measurements was 100 fps with an exposure time of 9.4 ms. The interrogation window size is 25 × 25 pixels (30 × 30 µm). The post-PIV spatial filtering was done using a 3 × 3 median filter. The vector was invalidated if the magnitude of difference of vector and median of the surrounding valid vectors was larger than three pixels. Also, the invalid vectors were replaced by the average of surrounding four valid vectors. We did not use any temporal smoothing for the PIV data.

6.6. Adhesion force [ F a ]

For measuring adhesion force, during peak of bubbling, different centrifuge tubes (10 ml YPD broth with initial yeast concentration of 10 4 cells ml −1 , 15 ml Centrifuge Tube, CORNING) were subjected to increasing magnitudes of centrifugation for 5 min. The number of yeasts were counted using a cell counting plate by taking out an aliquot of 10 µl near the foam–fluid interface with the help of a micropipette. These cells represent yeasts adhered to the bubbles. The centrifugation strength G for which such cell count becomes zero was taken as the threshold which is needed to separate all yeasts from the bubbles, which is ultimately used to calculate the adhesion force between yeast and bubbles.

6.7. Yeast group size [ N ( t )]

To track these variations in sizes of suspended yeast groups in terms of number of cells N , we drew aliquots of 10 µl at different time instants over 3 days from the unstirred flask in fermentation and counted the average number of cells in yeast groups N using a cell counting plate.

6.8. Yeasts in bubble layer [ c b ]

In this set of experiments, we counted the yeast concentration in bubble layer just above the interface by drawing a known volume of the foam. It was made sure that only bubbles were drawn. Since we know the average bubble diameter (306.8 ± 29.1 µm) in the bubble layer (through horizontal microscope), the number of yeasts adhered to a single bubble in the bubble layer can be estimated, i.e. c b .

6.9. Numerical methods

We used FVM for solving the governing equation (i.e. eq. (5)) using open access computation software SCILAB. The fluid layer and the bubble layer were divided into 120 and 20 elements, respectively, with homogeneous intervals, each 0.5 mm apart. The third-order upwind scheme (QUICK) was used for discretization of advection terms, whereas the second-order central differencing scheme was used for diffusion term discretization. Time-marching was performed using the explicit Euler method with a time step of 20 s for 80 h. More details of our discretization procedure can be found in electronic supplementary material, document (S3).

Supplementary Material

Data accessibility.

The underlying data behind the figures can be accessed at: https://doi.org/10.6084/m9.figshare.12197859.v4 .

Authors' contributions

T.I., K.K. and A.S. formulated and designed the research. A.S. performed simulations and experiments with inputs from T.I. and K.K. All authors were involved in data interpretation and manuscript preparation.

Competing interests

Authors declare no competing interests.

The authors acknowledge the support of Japan Society for the Promotion of Science KAKENHI (grants nos. 17H00853 and 19H02059).

1. Walls PLL, Bird JC, Bourouiba L. 2014. Moving with bubbles: a review of the interactions between bubbles and the microorganisms that surround them. Integr. Comp. Biol. 54, 1014–1025. ( 10.1093/icb/icu100) [ DOI ] [ PubMed ] [ Google Scholar ]
2. Poulain S, Bourouiba L. 2019. Disease transmission via drops and bubbles. Phys. Today. 72, 70–71. ( 10.1063/PT.3.4211) [ DOI ] [ Google Scholar ]
3. Rubio J, Carissimi E, Rosa JJ. 2007. Flotation in water and wastewater treatment and reuse: recent trends in Brazil. Int. J. Environ. Pollut. 30, 197 ( 10.1504/IJEP.2007.014700) [ DOI ] [ Google Scholar ]
4. Schmideder S, Kirse C, Hofinger J, Rollié S, Briesen H. 2018. Modeling the separation of microorganisms in bioprocesses by flotation. Processes 6, 184 ( 10.3390/pr6100184) [ DOI ] [ Google Scholar ]
5. Barnett JA. 2003. A history of research on yeasts 5: the fermentation pathway. Yeast 20, 509–543. ( 10.1002/yea.986) [ DOI ] [ PubMed ] [ Google Scholar ]
6. McGovern PE, et al. 2004. Fermented beverages of pre-and proto-historic China. Proc. Natl Acad. Sci. USA 101, 17 593–17 598. ( 10.1073/pnas.0407921102) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
7. Jelinek B. 1946. Top and bottom fermentation systems and their respective beer characteristics. J. Inst. Brew. 52, 174–181. ( 10.1002/j.2050-0416.1946.tb01579.x) [ DOI ] [ Google Scholar ]
8. Bryan AK, Goranov A, Amon A, Manalis SR. 2010. Measurement of mass, density, and volume during the cell cycle of yeast. Proc. Natl Acad. Sci. USA 107, 999–1004. ( 10.1073/pnas.0901851107) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
9. Palmieri MC, Greenhalf W, Laluce C. 1996. Efficient flotation of yeast cells grown in batch culture. Biotechnol. Bioeng. 50, 248–256. () [ DOI ] [ PubMed ] [ Google Scholar ]
10. Dengis PB, Rouxhet PG. 1997. Surface properties of top- and bottom-fermenting yeast. Yeast 13, 931–943. () [ DOI ] [ PubMed ] [ Google Scholar ]
11. DeSousa SR, Oliveira KF, Souza CS, Kilikian BV, Laluce C. 2003. Yeast flotation viewed as the result of the interplay of supernatant composition and cell-wall hydrophobicity. Colloids Surf. B Biointerfaces 29, 309–319. ( 10.1016/S0927-7765(03)00019-5) [ DOI ] [ Google Scholar ]
12. Ditscherlein L, Jolan Gulden S, Müller S, Baumann RP, Peuker UA, Nirschl H. 2018. Measuring interactions between yeast cells and a micro-sized air bubble via atomic force microscopy. J. Colloid Interface Sci. 532, 689–699. ( 10.1016/j.jcis.2018.08.031) [ DOI ] [ PubMed ] [ Google Scholar ]
13. Yumiyama S, Kato S, Konishi Y, Nomura T. 2019. Direct measurement of interaction forces between a yeast cell and a microbubble using atomic force microscopy. Colloids Surf. A Physicochem. Eng. Asp. 583, 123963 ( 10.1016/j.colsurfa.2019.123963) [ DOI ] [ Google Scholar ]
14. Bishop LR. 1938. Part I: The natural history of a brewery top fermentation. J. Inst. Brew. 44, 70–73. ( 10.1002/j.2050-0416.1938.tb05834.x) [ DOI ] [ Google Scholar ]
15. Delente J, Akin C, Krabbe E, Ladenburg K. 1969. Fluid dynamics of anaerobic fermentation. Biotechnol. Bioeng. 11, 631–646. ( 10.1002/bit.260110410) [ DOI ] [ PubMed ] [ Google Scholar ]
16. Garcia AI, García LA, Diaz M. 1993. Mixing in unstirred batch fermenters. Chem. Eng. J. 51, B57–B61. ( 10.1016/0300-9467(93)80031-I) [ DOI ] [ Google Scholar ]
17. Garcia AI, Pandiella SS, Garcia LA, Diaz M. 1994. Mechanism for mixing and homogenization in beer fermentation. Bioprocess. Eng. 10, 179–184. ( 10.1007/BF00387527) [ DOI ] [ Google Scholar ]
18. Díaz M, García AI, García LA. 1996. Mixing power, external convection, and effectiveness in bioreactors. Biotechnol. Bioeng. 51, 131–140. () [ DOI ] [ PubMed ] [ Google Scholar ]
19. Meironke H. 2014. Experimental studies of convection flow during the fermentation process of beer by means of ultrasonic Doppler velocimetry. In 9th International Symposium on Ultrasonic Doppler Methods for Fluid Mechancs and Fluid Engineering, Strasbourg, France, 27–29 August See https://www.isud-conference.org/proc/#isud9 . [ Google Scholar ]
20. Zhang HL, Baeyens J, Tan TW. 2012. The bubble-induced mixing in starch-to-ethanol fermenters. Chem. Eng. Res. Des. 90, 2122–2128. ( 10.1016/j.cherd.2012.05.003) [ DOI ] [ Google Scholar ]
21. Schmidt D, Velten K. 2016. Numerical simulation of bubble flow homogenization in industrial scale wine fermentations. Food Bioprod. Process. 100, 102–117. ( 10.1016/j.fbp.2016.06.008) [ DOI ] [ Google Scholar ]
22. Vlassides S, Block DE. 2000. Evaluation of cell concentration profiles and mixing in unagitated wine fermentors. Am. J. Enol. Vitic. 51, 73–80. [ Google Scholar ]
23. Schwinn M, Durner D, Delgado A, Fischer U. 2019. Distribution of yeast cells, temperature, and fermentation by-products in white wine fermentations. Am. J. Enol. Vitic. 70, 339–350 ( 10.5344/ajev.2019.18092) [ DOI ] [ Google Scholar ]
24. De La Roza C, Laca A, Garcia LA, Diaz M.. 2002. Stirring and mixing effects at different cider fermentation scales. Food Bioprod. Process. 80, 129–134. ( 10.1205/09603080252938762) [ DOI ] [ Google Scholar ]
25. Hepworth N, Brown AK, Hammond JRM, Boyd JWR, Varley J. 2003. The use of laboratory-scale fermentations as a tool for modelling beer fermentations. Food Bioprod. Process. 81, 50–56. ( 10.1205/096030803765208661) [ DOI ] [ Google Scholar ]
26. Klembt D, Meironke H. 2019. Numerical approaches for the simulation of the yeast distribution in a fermentation tank. PAMM 19, e20190011 ( 10.1002/pamm.201900116) [ DOI ] [ Google Scholar ]
27. Stahl G, Ben Salem SN, Chen L, Zhao B, Farabaugh PJ. 2004. Translational accuracy during exponential, postdiauxic, and stationary growth phases in Saccharomyces cerevisiae . Eukaryot. Cell 3, 331–338. ( 10.1128/EC.3.2.331) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
28. Lavová B, Urminská D, Šillerová S, Blažena I. 2014. Diauxic growth of Saccharomyces cerevisiae . J. Microbiol. Biotechnol. Food Sci. 3, 122–123. [ Google Scholar ]
29. Galdieri L, Mehrotra S, Yu S, Vancura A. 2010. Transcriptional regulation in yeast during diauxic shift and stationary phase. Omi. J. Integr. Biol. 14, 629–638. ( 10.1089/omi.2010.0069) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
30. Vachaparambil KJ, Einarsrud KE. 2018. Explanation of bubble nucleation mechanisms: a gradient theory approach. J. Electrochem. Soc. 165, E504–E512. ( 10.1149/2.1031810jes) [ DOI ] [ Google Scholar ]
31. Weber ME, Bhaga D. 1982. Fluid drift caused by a rising bubble. Chem. Eng. Sci. 37, 113–116. ( 10.1016/0009-2509(82)80073-0) [ DOI ] [ Google Scholar ]
32. Risso F. 2018. Agitation, mixing, and transfers induced by bubbles. Annu. Rev. Fluid Mech. 50, 25–48. ( 10.1146/annurev-fluid-122316-045003) [ DOI ] [ Google Scholar ]
33. Brücker C. 1999. Structure and dynamics of the wake of bubbles and its relevance for bubble interaction. Phys. Fluids 11, 1781–1796. ( 10.1063/1.870043) [ DOI ] [ Google Scholar ]
34. Van Wijngaarden L. 1998. On pseudo turbulence. Theor. Comput. Fluid Dyn. 10, 449–458. ( 10.1007/s001620050076) [ DOI ] [ Google Scholar ]
35. Martínez-Mercado J, Palacios-Morales CA, Zenit R. 2007. Measurement of pseudoturbulence intensity in monodispersed bubbly liquids for 10 < Re < 500. Phys. Fluids 19, 103302 ( 10.1063/1.2772256) [ DOI ] [ Google Scholar ]
36. Cartellier A, Rivíère N. 2001. Bubble-induced agitation and microstructure in uniform bubbly flows at small to moderate particle Reynolds numbers. Phys. Fluids 13, 2165–2181. ( 10.1063/1.1381562) [ DOI ] [ Google Scholar ]
37. Alméras E, Plais C, Euzenat F, Risso F, Roig V, Augier F. 2016. Scalar mixing in bubbly flows: experimental investigation and diffusivity modelling. Chem. Eng. Sci. 140, 114–122. ( 10.1016/j.ces.2015.10.010) [ DOI ] [ Google Scholar ]
38. Mudde RF. 2005. Gravity-driven bubbly flows. Annu. Rev. Fluid Mech. 37, 393–423. ( 10.1146/annurev.fluid.37.061903.175803) [ DOI ] [ Google Scholar ]
39. Degaleesan S, Duduković MP. 1998. Liquid backmixing in bubble columns and the axial dispersion coefficient. AIChE J. 44, 2369–2378. ( 10.1002/aic.690441105) [ DOI ] [ Google Scholar ]
40. Parkinson L, Sedev R, Fornasiero D, Ralston J. 2008. The terminal rise velocity of 10–100 µm diameter bubbles in water. J. Colloid Interface Sci. 322, 168–172. ( 10.1016/j.jcis.2008.02.072) [ DOI ] [ PubMed ] [ Google Scholar ]
41. Walls PLL, Bird JC. 2017. Enriching particles on a bubble through drainage: measuring and modeling the concentration of microbial particles in a bubble film at rupture. Elem. Sci. Anth. 5, 34 ( 10.1525/elementa.230) [ DOI ] [ Google Scholar ]
42. Zhao XQ, Bai FW. 2009. Yeast flocculation: new story in fuel ethanol production. Biotechnol. Adv. 27, 849–856. ( 10.1016/j.biotechadv.2009.06.006) [ DOI ] [ PubMed ] [ Google Scholar ]
43. Saffman PG, Delbrück M.. 1975. Brownian motion in biological membranes. Proc. Natl Acad. Sci. USA 72, 3111–3113. ( 10.1073/pnas.72.8.3111) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
44. Cheung C, Hwang YH, Wu XL, Choi HJ. 1996. Diffusion of particles in free-standing liquid films. Phys. Rev. Lett. 76, 2531–2534. ( 10.1103/PhysRevLett.76.2531) [ DOI ] [ PubMed ] [ Google Scholar ]
45. Speers RA, Wan Y, Jin Y, Stewart RJ. 2006. Effects of fermentation parameters and cell wall properties on yeast flocculation 1. J. Inst. Brew. 112, 246–254. ( 10.1002/j.2050-0416.2006.tb00720.x) [ DOI ] [ Google Scholar ]
46. Aben RCH, et al. 2017. Cross continental increase in methane ebullition under climate change. Nat. Commun. 8, 1–8. ( 10.1038/s41467-017-01535-y) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]
47. Nonaka Y, Kikuchi K, Numayama-Tsuruta K, Kage A, Ueno H, Ishikawa T. 2016. Inhomogeneous distribution of Chlamydomonas in a cylindrical container with a bubble plume. Biol. Open 5, 154–160. ( 10.1242/bio.015669) [ DOI ] [ PMC free article ] [ PubMed ] [ Google Scholar ]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Data availability statement.

View on publisher site
PDF (1.4 MB)
Collections