sand pile experiment

April 7, 2014

Sand Pile Model of the Mind Grows in Popularity

Support is growing for a decades-old physics idea suggesting that localized episodes of disordered brain activity help keep the overall system in healthy balance

By Jennifer Ouellette & Quanta Magazine

From Quanta Magazine ( find original story here ).

In 1999, the Danish physicist Per Bak proclaimed to a group of neuroscientists that it had taken him only 10 minutes to determine where the field had gone wrong. Perhaps the brain was less complicated than they thought, he said. Perhaps, he said, the brain worked on the same fundamental principles as a simple sand pile, in which avalanches of various sizes help keep the entire system stable overall — a process he dubbed “self-organized criticality.”

As much as scientists in other fields adore outspoken, know-it-all physicists, Bak’s audacious idea — that the brain’s ordered complexity and thinking ability arise spontaneously from the disordered electrical activity of neurons — did not meet with immediate acceptance.

On supporting science journalism

If you're enjoying this article, consider supporting our award-winning journalism by subscribing . By purchasing a subscription you are helping to ensure the future of impactful stories about the discoveries and ideas shaping our world today.

But over time, in fits and starts, Bak’s radical argument has grown into a legitimate scientific discipline. Now, about 150 scientists worldwide investigate so-called “critical” phenomena in the brain, the topic of at least three focused workshops in 2013 alone. Add the ongoing efforts to found a journal devoted to such studies, and you have all the hallmarks of a field moving from the fringes of disciplinary boundaries to the mainstream.

In the 1980s, Bak first wondered how the exquisite order seen in nature arises out of the disordered mix of particles that constitute the building blocks of matter. He found an answer in phase transition, the process by which a material transforms from one phase of matter to another. The change can be sudden, like water evaporating into steam, or gradual, like a material becoming superconductive. The precise moment of transition — when the system is halfway between one phase and the other — is called the critical point, or, more colloquially, the “tipping point.”

Classical phase transitions require what is known as precise tuning: in the case of water evaporating into vapor, the critical point can only be reached if the temperature and pressure are just right. But Bak proposed a means by which simple, local interactions between the elements of a system could spontaneously reach that critical point — hence the term self-organized criticality.

Think of sand running from the top of an hourglass to the bottom. Grain by grain, the sand accumulates. Eventually, the growing pile reaches a point where it is so unstable that the next grain to fall may cause it to collapse in an avalanche. When a collapse occurs, the base widens, and the sand starts to pile up again — until the mound once again hits the critical point and founders. It is through this series of avalanches of various sizes that the sand pile — a complex system of millions of tiny elements — maintains overall stability.

While these small instabilities paradoxically keep the sand pile stable, once the pile reaches the critical point, there is no way to tell whether the next grain to drop will cause an avalanche — or just how big any given avalanche will be. All one can say for sure is that smaller avalanches will occur more frequently than larger ones, following what is known as a power law.

Bak introduced self-organized criticality in a  landmark 1987 paper  — one of the most highly cited physics papers of the last 30 years. Bak began to see the stabilizing role of frequent smaller collapses wherever he looked. His 1996 book, “How Nature Works,” extended the concept beyond simple sand piles to other complex systems: earthquakes, financial markets, traffic jams, biological evolution, the distribution of galaxies in the universe — and the brain. Bak’s hypothesis implies that most of the time, the brain teeters on the edge of a phase transition, hovering between order and disorder.

The brain is an incredibly complex machine. Each of its tens of billions of neurons is connected to thousands of others, and their interactions give rise to the emergent process we call “thinking.” According to Bak, the electrical activity of brain cells shift back and forth between calm periods and avalanches — just like the grains of sand in his sand pile — so that the brain is always balanced precariously right at that the critical point.

A better understanding of these critical dynamics could shed light on what happens when the brain malfunctions. Self-organized criticality also holds promise as a unifying theoretical framework. According to the neurophysiologist  Dante Chialvo , most of the current models in neuroscience apply only to single experiments; to replicate the results from other experiments, scientists must change the parameters — tune the system — or use a different model entirely.

Self-organized criticality has a certain intuitive appeal. But a good scientific theory must be more than elegant and beautiful. Bak’s notion has had its share of critics, in part because his approach strikes many as ridiculously broad: He saw nothing strange about leaping across disciplinary boundaries and using self-organized criticality to link the dynamics of forest fires, measles and the large-scale structure of the universe — often in a single talk. Nor was he one to mince words. His abrasive personality did not endear him to his critics, although  Lee Smolin , a physicist at the Perimeter Institute for Theoretical Physics, in Canada, has chalked this up to “childlike simplicity,” rather than arrogance. “It would not have occurred to him that there was any other way to be,” Smolin wrote in a remembrance after  Bak’s death in 2002 . “Science is hard, and we have to say what we think.”

Nonetheless, Bak’s ideas found fertile ground in a handful of like-minded scientists. Chialvo, now with the University of California, Los Angeles, and with the National Scientific and Technical Research Council in Argentina, met Bak at Brookhaven National Laboratory around 1990 and became convinced that self-organized criticality could explain brain activity. He, too, encountered considerable resistance. “I had to put up with a number of critics because we didn’t have enough data,” Chialvo said. Dietmar Plenz , a neuroscientist with the National Institute of Mental Health, recalled that it was impossible to win a grant in neuroscience to work on self-organized criticality at the time, given the lack of experimental evidence.

Since 2003, however, the body of evidence showing that the brain exhibits key properties of criticality has grown, from examinations of slices of cortical tissue and electroencephalography (EEG) recordings of the interactions between individual neurons to large-scale studies comparing the predictions of computer models with data from functional magnetic resonance (fMRI) imaging. “Now the field is mature enough to stand up to any  fair criticism ,” Chialvo said.

One of the first empirical tests of Bak’s sand pile model  took place in 1992 , in the physics department of the University of Oslo. The physicists confined piles of rice between glass plates and added grains one at a time, capturing the resulting avalanche dynamics on camera. They found that the piles of elongated grains of rice behaved much like Bak’s simplified model.

Most notably, the smaller avalanches were more frequent than the larger ones, following the expected power law distribution. That is, if there were 100 small avalanches involving only 10 grains during a given time frame, there would be 10 avalanches involving 100 grains in the same period, but only a single large avalanche involving 1,000 grains. (The same pattern had been observed in earthquakes and their aftershocks. If there are 100 quakes measuring 6.0 on the Gutenberg-Richter scale in a given year, there will be 10 7.0 quakes and one 8.0 quake.)

Ten years later, Plenz and a colleague, John Beggs , now a biophysicist at Indiana University,  observed the same pattern of avalanches  in the electrical activity of neurons in cortical slices — the first key piece of evidence that the brain functions at criticality. “It was something that no one believed the brain would do,” Plenz said. “The surprise is that is exactly what happens.”  Studies using magnetoencephalography  (MEG) and  Chialvo’s own work  comparing computer simulations with fMRI imaging data of the brain’s resting state have since added to the evidence that the brain exhibits these key avalanche dynamics.

But perhaps it is not so surprising. There can be no phase transitions without a critical point, and without transitions, a complex system — like Bak’s sand pile, or the brain — cannot adapt. That is why avalanches only show up at criticality, a “sweet spot” where a system is perfectly balanced between order and disorder, according to Plenz. They typically occur when the brain is in its normal resting state. Avalanches are a mechanism by which a complex system avoids becoming trapped, or “phase-locked,” in one of two extreme cases. At one extreme, there is too much order, such as during an epileptic seizure; the interactions among elements are too strong and rigid, so the system cannot adapt to changing conditions. At the other, there is too much disorder; the neurons aren’t communicating as much, or aren’t as broadly interconnected throughout the brain, so information can’t spread as efficiently and, once again, the system is unable to adapt.

A complex system that hovers between “boring randomness and boring regularity” is surprisingly stable overall, said  Olaf Sporns , a cognitive neuroscientist at Indiana University. “Boring is bad,” he said, at least for a critical system. In fact, “if you try to avoid ever sparking an avalanche, eventually when one does occur, it is likely to be really large,” said  Raissa D’Souza , a complex systems scientist at the University of California, Davis, who simulated just such a generic system last year. “If you spark avalanches all the time, you’ve used up all the fuel, so to speak, and so there is no opportunity for large avalanches.”

D’Souza’s research  applies these dynamics to better understand power outages across the electrical grid. The brain, too, needs sufficient order to function properly, but also enough flexibility to adapt to changing conditions; otherwise, the organism could not survive. This could be one reason that the brain exhibits hallmarks of self-organized criticality: It confers an evolutionary advantage. “A brain that is not critical is a brain that does exactly the same thing every minute, or, in the other extreme, is so chaotic that it does a completely random thing, no matter what the circumstances,” Chialvo said. “That is the brain of an idiot.”

When the brain veers away from criticality, information can no longer percolate through the system as efficiently. One study (not yet published) examined sleep deprivation; subjects remained awake for 36 hours and then took a reaction time test while an EEG monitored their brain activity. The more sleep-deprived the subject, the more the person’s brain activity veered away from the critical balance point and the worse the performance on the test.

Another study  collected data from epileptic subjects during seizures. The EEG recordings revealed that mid-seizure, the telltale avalanches of criticality vanished. There was too much synchronization among neurons, and then, Plenz said, “information processing breaks down, people lose consciousness, and they don’t remember what happened until they recover.”

Chialvo envisions self-organized criticality providing a broader, more fundamental theory for neuroscientists, like those found in physics. He believes it could be used to model the mind in all its possible states: awake, asleep, under anesthesia, suffering a seizure, and under the influence of a psychedelic drug, among many others.

This is especially relevant as neuroscience  moves deeper into the realm of big data . The latest advanced imaging techniques are capable of mapping synapses and monitoring brain activity at unprecedented resolutions, with a corresponding explosion in the size of data sets. Billions of dollars in research funding has launched the  Human Connectome Project  — which aims to build a “network map” of neural pathways in the brain — and the  Brain Research Through Advancing Innovative Neurotechnologies  (BRAIN), dedicated to developing new technological tools for recording signals from cells. There is also Europe’s  Human Brain Project , working to simulate the complete human brain on a supercomputer, and China’s  Brainnetome project to integrate data collected from every level of the brain’s hierarchy of complex networks.

But without an underlying theory, it will be difficult to glean all the potential insights hidden in the data. “It is fine to build maps and it is fine to catalog pieces and how they are related, so long as you don’t lose track of the fact that when the system you map actually functions, it is in an integrated system and it is dynamic,” Sporns said.

“The structure of the brain — the precise map of who connects with whom — is almost irrelevant by itself,” Chialvo said — or rather, it is necessary but not sufficient to decipher how cognition and behavior are generated in the brain. “What is relevant is the dynamics,” Chialvo said. He then compared the brain with a street map of Los Angeles containing details of all the connections at every scale, from private driveways to public freeways. The map tells us only about the structural connections; it does not help predict how traffic moves along those connections or where (and when) a traffic jam is likely to form. The map is static; traffic is dynamic. So, too, is the activity of the brain. In recent work, Chialvo said, researchers have demonstrated that both traffic dynamics and brain dynamics exhibit criticality.

Sporns emphasizes that it remains to be seen just how robust this phenomenon might be in the brain, pointing out that more evidence is needed beyond the observation of power laws in brain dynamics. In particular, the theory still lacks a clear description for how criticality arises from neurobiological mechanisms — the signaling of neurons in local and distributed circuits. But he admits that he is rooting for the theory to succeed. “It makes so much sense,” he said. “If you were to design a brain, you would probably want criticality in the mix. But ultimately, it is an empirical question.”

Reprinted with permission from Quanta Magazine , an editorially independent division of SimonsFoundation.org whose mission is to enhance public understanding of science by covering research developments and trends in mathematics and the physical and life sciences.

• Published: 20 June 2014

A sandpile experiment and its implications for self-organized criticality and characteristic earthquake

• Naoto Yoshioka 1  

Earth, Planets and Space volume  55 ,  pages 283–289 ( 2003 ) Cite this article

3076 Accesses

17 Citations

Metrics details

We have performed an experiment in which a conical sandpile was built by slowly dropping sand onto a circular disk through a funnel with a small outlet. Avalanches (sand dropping off the disk) occurred, the size and the number of which were observed. It was seen that the behavior of avalanches (frequency-size distribution) was determined solely by the ratio of grain size to disk size, which is consistent with earlier studies. We categorize the behavior into three types: (1) the self-organized criticality (SOC) type (obeying Gutenberg-Richter’s law), (2) the characteristic earthquake (CE) type where only large avalanches are almost periodically generated, and (3) the transition type. The transition from SOC to CE type drastically occurs when the ratio of grain diameter to disk radius is reduced to about 0.02. The underlying mechanism to cause the transition is considered. Results of simulation by cellular automaton models, an experimental result showing that a conical pile has a stress dip near its center, and a two-dimensional simulation building up a conical pile, all suggest that the transition occurs due to a change in stress profile inside and near the surface of the pile. Although we are unfortunately not able to understand the detailed mechanism at the present stage, it seems very important to further investigate the underlying physics of the transition because it presumably provides us a clue to understand the mechanism of the periodicity of large characteristic earthquakes and may open a way for earthquake prediction.

Ando, M., Source mechanisms and tectonic significance of historical earthquakes along the Nankai trough, Japan, Tectonophys , 27 , 119–140, 1975.

Article   Google Scholar  

Bak, P. and C. Tang, Earthquakes as a self-organized critical phenomena, J. Geophys. Res. , 94 , 15635–15637, 1989.

Bak, P., C. Tang, and K. Wiesenfeld, Self-organized criticality: An explanation of 1/f noise, Phys. Rev. Lett. , 59 , 381–384, 1987.

Bak, P., C. Tang, and K. Wiesenfeld, Self-organized criticality, Phys. Rev. A , 38 , 364–374, 1988.

Barriere, B. and D. L. Turcotte, Seismicity and self-organized criticality, Phys. Rev. E , 49 , 1151–1160, 1994.

Burridge, R. and L. Knopoff, Model and theoretical seismicity, Bull. Seism. Soc. Am. , 57 , 341–371, 1967.

Google Scholar  

Carlson, J. M. and J. S. Langer, Properties of earthquakes generated by fault dynamic, Phys. Rev. Lett. , 62 , 2632–2635, 1989a.

Carlson, J. M. and J. S. Langer, Mechanical model of an earthquake fault, Phys. Rev. A , 40 , 6470–6484, 1989b.

Evesque, P., Analysis of the statistics of sandpile avalanches using soil-mechanics results and concepts, Phys. Rev. A , 43 , 2720–2740, 1991.

Geller, R, J., D. D. Jackson, Y. Y. Kagan, and F. Mulargia, Earthquake cannot be predicted, Science , 275 , 1616–1617, 1997.

Held, G. A., D. H. Solina, D. T. Keane, W. J. Haag, P. M. Horn, and G. Grinstein, Experimental study of critical-mass fluctuations in an evolving sandpile, Physical Rev. Lett. , 65 , 1120–1123, 1990.

Ito, K. and M. Matsuzaki, Earthquakes as self-organized critical phenomena, J. Geophys. Res. , 95 , 6853–6860, 1990.

Jaeger, H. M., Ch. Liu, and S. R. Nagel, Relaxation at the angle of repose, Phys. Rev. Lett. , 62 , 40–43, 1989.

Jotaki, T. and R. Moriyama, On the bottom pressure distribution of the bulk materials piled with the angle of repose, J. Soc. Powder Technol. Japan , 60 , 184–191, 1979 (in Japanese with English abstract and figure caption).

Kadanoff, L. P., S. R. Nagel, L. Wu, and Sm. Zhou, Scaling and universality in avalanches, Phys. Rev. A , 39 , 6524–6537, 1989.

Kumagai, H., Time sequence and the recurrence models for large earthquakes along the Nankai trough revisited, Geophys. Res. Lett. , 23 , 1139–1142, 1996.

Liu, Ch., H. M. Jaeger, and S. R. Nagel, Finite-size effects in a sandpile, Phys. Rev. A , 43 , 7091–7092, 1991.

Matuttis, H. G., Simulation of the pressure distribution under a two-dimensional heap of polygonal particles, Granular Matter , 1 , 83–91, 1998.

Nagel, S. R., Instabilities in a sandpile, Rev. Modern Phys. , 64 , 321–325, 1992.

Nakanishi, H., Cellular-automaton model of earthquakes with deterministic dynamics, Phys. Rev. A , 41 , 7086–7089, 1990.

Nakanishi, H., Statistical properties of the cellular-automaton model for earthquakes, Phys. Rev. A , 43 , 6613–6621, 1991.

Rosendahl, J., M. Vekic, and J. Kelly, Persistent self-organization of sand-piles, Phys. Rev. E , 47 , 1401–1404, 1993.

Rosendahl, J., M. Vekic, and J. E. Rutledge, Predictability of large avalanches on a sandpiles, Phys. Rev. Lett. , 73 , 537–540, 1994.

Schinner, A., H.-G. Matuttis, T. Akiyama, J. Aoki, S. Takahashi, K. M. Aoki, and K. Kassner, History-dependent structure in granular piles, in Powder and Grains 2001 , edited by Swets and Zeitlinger, pp. 499–502, 2001.

Schwartz, D. P. and K. J. Coppersmith, Fault behavior and characteristic earthquakes: Examples from the Wasatch and San Andreas fault zones, J. Geophys. Res. , 89 , 5681–5698, 1984.

Shimazaki, K., The almighty earthquake, Seism. Res. Lett. , 70 , 147–148, 1999.

Shimazaki, K. and T. Nakata, Time-predictable recurrence model for large earthquakes, Geophys. Res. Lett. , 7 , 279–282, 1980.

Stirling, M. W., S. G. Wesnousky, and K. Shimazaki, Fault trace complexity, cumulative slip, and shape of the magnitude-frequency distribution for stick-slip faults: a global survey, Geophys. J. Int. , 124 , 833–868, 1996.

Turcotte, D. L., Self-organized criticality, Rep. Prog. Phys. , 62 , 1377–1429, 1999.

Vanel, L., D. Howell, D. Clark, R. P. Behringer, and E. Clement, Memories in sand: Experimental tests of construction history on stress distributions under sandpile, Phys. Rev. E , 60 , R5040–R5043, 1999.

Wesnousky, S. G., C. H. Scholz, K. Shimazaki, and T. Matsuda, Earthquake frequency distribution and the mechanics of faulting, J. Geophys. Res. , 88 , 9331–9340, 1983.

Download references

Author information

Authors and affiliations.

Graduate School of Integrated Science, Yokohama City University, Seto 22-2, Kanazawaku, Yokohama, 236-0027, Japan

Naoto Yoshioka

You can also search for this author in PubMed   Google Scholar

Corresponding author

Correspondence to Naoto Yoshioka .

Rights and permissions

Reprints and permissions

About this article

Cite this article.

Yoshioka, N. A sandpile experiment and its implications for self-organized criticality and characteristic earthquake. Earth Planet Sp 55 , 283–289 (2003). https://doi.org/10.1186/BF03351762

Download citation

Received : 14 February 2003

Revised : 07 July 2003

Accepted : 08 July 2003

Published : 20 June 2014

Issue Date : June 2003

DOI : https://doi.org/10.1186/BF03351762

Share this article

Anyone you share the following link with will be able to read this content:

Sorry, a shareable link is not currently available for this article.

Provided by the Springer Nature SharedIt content-sharing initiative

• self-organized criticality
• characteristic earthquake

Functioning brain follows famous sand pile model

Experiments show for the first time that the model describes activity in brain tissue processing sensory input

One of the deep problems in understanding the brain is to understand how relatively simple computing units (the neurons), collectively perform extremely complex operations (thinking).

In 1999, Danish scientist Per Bak made the startling proposal that the brain worked in much the same way as a sand pile. As more sand is added to the pile, many small avalanches keep the entire pile stable. Similarly, electrical avalanches in the brain hold it at a balance point, or critical point, where information processing is optimized.

The model is intuitively attractive and experiments with isolated slices of brain tissue have indeed shown that spontaneous electrical activity displays the statistical hallmarks of criticality, which seems to be the brain’s normal, or resting, state.

But there was a piece missing, said Ralf Wessel, PhD, associate professor of physics in Arts & Sciences at Washington University in St. Louis. “On the one hand, the hypothesis was that, at criticality, the brain is optimized for computation. On the other hand, people had only studied brain tissue that wasn’t actually doing anything,” he said.

“We wondered what would happen if the brain had a job to do, if there were sensory input it had to process. Would the brain still operate at criticality?”

To find out, Wessel’s lab at Washington University and Woodrow Shew’s lab at the University of Arkansas collaborated to monitor electrical activity in the visual cortex when a series of moving images played across the retina.

As they report online in the June 22 issue of Nature Physics , the sensory input momentarily pushed the cortex away from criticality but, no matter what the input, the cortex spontaneously returned to the critical regime.

“The system naturally adapts to input,” said Shew, an assistant professor of physics at the University of Arkansas, “tuning itself back into a good state for handling the input and making sense of it.”

“In the future, brain dynamics might serve as a biomarker for health or disease,” said Yahya Karimipanah, a graduate student in physics in Arts & Sciences at Washington University in St. Louis and a co-author on the paper.

When people are sleep-deprived, he said, recordings indicate the electrical activity in their brains is subcritical. On the other hand, the uncontrolled firing during an epileptic seizure is a manifestation of supercritical dynamics.

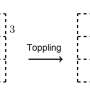
Talking about criticality The concept of criticality is central to the model. To explain criticality, Wessel uses the metaphor of a game played on a checkerboard of cells. “Suppose each cell of the checkerboard can hold up to three grains of sand before it ‘topples.’ When the fourth grain is added, the cell adds a grain of sand to each of its neighbors and if any of these neighbors are ‘full’ they redistribute sand to their neighbors as well.

“A neuron is like a square in the checkerboard,” he said. It sums its inputs and once it reaches a threshold, it fires, sometimes causing connected neurons to fire as well. “In that sense,” he said, “the checkerboard model is a perfect metaphor for the dynamics of the brain.”

At the start of the game, communication is very local. An avalanche travels only two or three cells and then stops. But when every cell is “loaded,” there’s a very good chance that an avalanche will travel across the network.

Criticality, Wessel said, is in the “Goldilocks region,” where the brain is neither too sluggish nor too reactive. Its hallmark is firing avalanches that follow what is known as a power law, where smaller avalanches occur more frequently than larger ones.

The checkerboard is subcritical when many of the squares hold few grains of sand and the addition of a grain doesn’t trigger an avalanche. It is supercritical when most of the cells have three grains already, so when a grain is added — boom — the activity travels everywhere.

“The checkerboard game illustrates how you can end up with something incredibly complex, by repeating the same simple rule over and over again,” Wessel said.

Shew explains that the shift from subcritical to supercritical dynamics in the checkerboard game is a version of a phase transition. “We experience phase transitions every day,” he said, “when liquid water evaporates and turns into vapor or freezes and turns into ice. Your brain can go through a phase transition, as well,” he said, “and that’s a bit more surprising, right?

“Of course I don’t mean that the brain can melt or freeze, but it can switch from orderly to disorderly behavior,” he said. “Both states or phases are less than optimal. An epileptic seizure is an example of an extreme level of order; all your neurons are doing the same thing together and that’s not good. You need a little bit of disorder for your brain to work effectively.

“In this paper we describe what happens to the visual system when you drive it really hard. Intense visual input pushes it into one of these phases that’s not computationally effective, at least briefly. But there’s a natural process by which it adapts, tuning itself so that it is back to a state where it can make sense of the input.

“That state is right at the boundary between two phases,” he said. “That’s what we mean by criticality, the tipping point between two very different ways of working. Somehow this system tunes itself not to one phase or the other, but into the boundary between two phases.

“That’s a surprising thing,” he said.

This explanation for how the brain works might seem outlandish at first, but on reflection it makes sense that a brain able to read a map one moment and identify Bach’s Sonata No. 1 in G minor the next would seek a dynamic tipping point where it would be poised to nimbly adjust to changes in input.

Latest from the Newsroom

Recent stories.

Vagus nerve stimulation relieves severe depression

NIH grant funds study of cerebral small vessel disease

$10.8 million grant supports cutting-edge leukemia research

WashU Experts

Can Trump bypass Senate approval of controversial Cabinet nominees?

‘X-odus’ creates growing challenges for brand marketing

How to depolarize social media

WashU in the News

Is ‘S.N.L.’ Too Online, or Are We All?

The New Jersey drone scare is a privacy wake-up call

In Port Labor Dispute, Trump Backed a Union That Courted Him

share this!

February 11, 2019

Famous 'sandpile model' shown to move like a traveling sand dune

by Institute of Science and Technology Austria

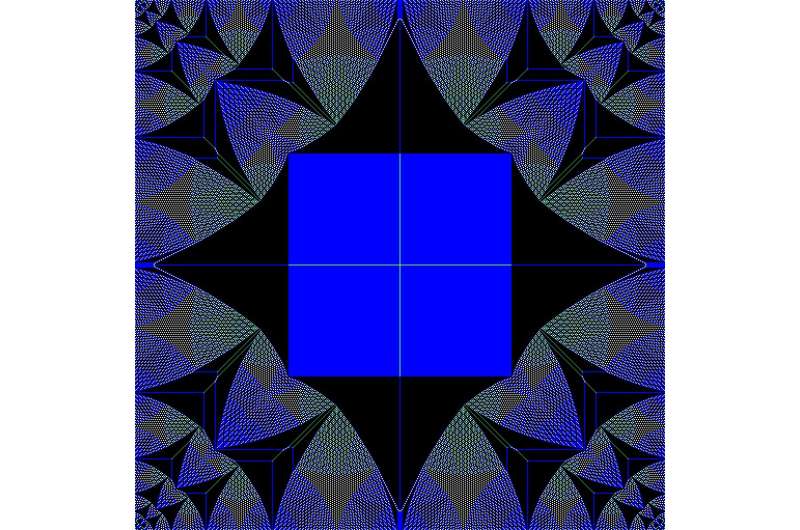
The so-called Abelian sandpile model has been studied by scientists for more than 30 years to better understand a physical phenomenon called self-organized criticality, which appears in many real-life situations such as the coordinated firing of brain cells, the spread of forest fires, the distribution of earthquake magnitudes, and even in the coordinated behavior of ant colonies. Even though the sandpile model serves as the archetypal model to study self-organized criticality, questions about its characteristics are still open and remain an active field of research.

Moritz Lang and Mikhail Shkonikov from the Institute of Science and Technology Austria (IST Austria) have now discovered a new property of this mathematical model: By adding sand grains in a specific manner to the sandpile, they induce dynamics reminiscent of the emergence, movement, collision and disappearance of sand dunes in the Gobi or the Namib desert. Unlike real-world sand dunes, however, the dunes in their work are composed of self-similar fractal patterns, somewhat similar to the famous Mandelbrot set. The results are published in the current issue of PNAS

The rules of the "sandpile experiment" are fairly simple: The model essentially consist of a grid of quadratic fields, similar to a checkerboard, onto which sand grains are dropped randomly. Fields that end up with fewer than four grains of sand remain stable, but when more grains accumulate on a field , it becomes unstable and topples. In such a toppling, four grains of sand are passed on to the four neighboring fields: one to the top, one to the bottom, one to the left, and one to the right. This might cause the neighboring fields to become unstable and topple, which then in turn may cause the next neighbors to topple, and so on—an "avalanche" results. Similar to real-world avalanches in the Alps, these "sandpile avalanches" have no characteristic size, and it is extremely challenging to predict if the next sand grain will cause a huge avalanche, or nothing at all.

De to the simplicity of these rules, the sandpile model is regularly used as an easy example in elementary programming courses. But it nevertheless displays various mathematical and physical phenomena still unexplained today, despite more than 30 years of extensive research. Among the most fascinating of these phenomena is the appearance of fractal sandpile configurations. These fractal sandpiles are characterized by self-similar patterns in which the same shapes appear repeatedly, but in increasingly smaller versions. The occurrence of these fractal patterns has yet to be explained mathematically. While the researchers at IST Austria did not solve this mathematical riddle, they rendered the phenomenon even more mysterious by showing that these fractal patterns can seemingly continuously transform into one another: They were able to capture video in which the fractal patterns display dynamics that are, depending on the background of the observer, either reminiscent of the movement of real-world sand dunes, or of psychedelic movies characteristic for the 1970s.

Deepening the mystery of a mathematical question may not be the ideal outcome. However, the two scientists, Moritz Lang and Mikhail Shkonikov, believe that their "psychedelic movies" might be the key to a better understanding the sandpile model , and maybe also of many other physical, biological or even economical problems.

Discover the latest in science, tech, and space with over 100,000 subscribers who rely on Phys.org for daily insights. Sign up for our free newsletter and get updates on breakthroughs, innovations, and research that matter— daily or weekly .

"You could say that we have found universal coordinates for the sandpile," say Mikhail Shkonikov. "Essentially, we can give every sand dune in the desert a very specific identifier." Moritz Lang, who is a theoretical biologist, adds: "The key to understanding any physical or biological phenomenon is to understand its consequences. The more consequences we know, the harder it becomes to develop a scientific hypothesis that is in agreement with all those consequences. In that sense, knowing all possible sand dunes and how they move represents a lot of constraints, and we hope that in the end, this will remove sufficient hay from the stack such that we can find the needle."

The two researchers see many applications in real-world problems like the prediction of earthquake magnitudes, the functioning of the human brain, physics, or even economics: "In all these fields, we find haystacks that look similar, very similar. Maybe it turns out that all haystacks are the same, and that there is only one needle to find."

Journal information: Proceedings of the National Academy of Sciences

Provided by Institute of Science and Technology Austria

Explore further

Feedback to editors

NASA's Parker Solar Probe aims to fly closer to the sun like never before

New superionic conducting electrolyte could enhance stability of all-solid-state lithium metal batteries

5 hours ago

Physicists measure quantum geometry for first time

The genomic journey of modern and archaic humans may be older than we thought

Dec 21, 2024

Introducing perceptein, a protein-based artificial neural network in living cells

Saturday Citations: Chicxulub meteorite found guilty; Good news and bad news for LLMs

Archaeological study documents rare Christian tattoo in medieval Nubia

Scientists observe 'negative time' in quantum experiments

Lab work digs into gullies seen on giant asteroid Vesta by NASA's Dawn

Researchers take 'significant leap forward' with quantum simulation of molecular electron transfer

Dec 20, 2024

Relevant PhysicsForums posts

Proving goldbach's conjecture by induction (or why it doesn't seem to work).

3 hours ago

A simple trigonometry problem: Put eight coins around a central coin

Dec 17, 2024

When are two vectors collinear and coplanar?

Dec 13, 2024

Tips on developing and improving number sense and basic math skills

Dec 12, 2024

I had a question about a way to write Euler's identity

Dec 11, 2024

Which conditions should I check to see if a quadrilateral is a square?

Dec 9, 2024

More from General Math

Related Stories

One fractal quantifies another, mathematicians find

Mar 11, 2015

Mathematicians propose first continuous self-organised criticality model

Sep 13, 2018

Self-organization of sandpile models

Mar 31, 2008

A theoretical analysis of sand mega-ripples

May 1, 2018

Where does the sand on Mars come from?

Oct 11, 2017

Do barchans birth or collide? Two papers have different stories

Sep 2, 2013

Recommended for you

How prepared are we for another pandemic? Study provides mathematical insights into airborne viral transmission

Dec 19, 2024

Can deep learning techniques predict sudden state transitions in nonlinear dynamical systems?

String figures shed light on cultural connections and the roots of mathematical reasoning

How much faster is a knight than a king? A mathematical study reveals the exact ratio

Mathematician solves the moving sofa problem

Mathematicians make leap in modeling human impact on climate

Dec 10, 2024

Let us know if there is a problem with our content

Use this form if you have come across a typo, inaccuracy or would like to send an edit request for the content on this page. For general inquiries, please use our contact form . For general feedback, use the public comments section below (please adhere to guidelines ).

Please select the most appropriate category to facilitate processing of your request

Thank you for taking time to provide your feedback to the editors.

Your feedback is important to us. However, we do not guarantee individual replies due to the high volume of messages.

E-mail the story

Your email address is used only to let the recipient know who sent the email. Neither your address nor the recipient's address will be used for any other purpose. The information you enter will appear in your e-mail message and is not retained by Phys.org in any form.

Newsletter sign up

Get weekly and/or daily updates delivered to your inbox. You can unsubscribe at any time and we'll never share your details to third parties.

More information Privacy policy

Donate and enjoy an ad-free experience

We keep our content available to everyone. Consider supporting Science X's mission by getting a premium account.

E-mail newsletter