problem solving in volume

Reset password New user? Sign up

Existing user? Log in

Volume Problem Solving

Already have an account? Log in here.

To solve problems on this page, you should be familiar with the following: Volume - Cuboid Volume - Sphere Volume - Cylinder Volume - Pyramid

This wiki includes several problems motivated to enhance problem-solving skills. Before getting started, recall the following formulas:

• Volume of sphere with radius \(r:\) \( \frac43 \pi r^3 \)
• Volume of cube with side length \(L:\) \( L^3 \)
• Volume of cone with radius \(r\) and height \(h:\) \( \frac13\pi r^2h \)
• Volume of cylinder with radius \(r\) and height \(h:\) \( \pi r^2h\)
• Volume of a cuboid with length \(l\), breadth \(b\), and height \(h:\) \(lbh\)

Volume Problem Solving - Basic

Volume - problem solving - intermediate, volume problem solving - advanced.

This section revolves around the basic understanding of volume and using the formulas for finding the volume. A couple of examples are followed by several problems to try.

Find the volume of a cube of side length \(10\text{ cm}\). \[\begin{align} (\text {Volume of a cube}) & = {(\text {Side length}})^{3}\\ & = {10}^{3}\\ & = 1000 ~\big(\text{cm}^{3}\big).\ _\square \end{align}\]

Find the volume of a cuboid of length \(10\text{ cm}\), breadth \(8\text{ cm}\). and height \(6\text{ cm}\). \[\begin{align} (\text {Area of a cuboid}) & = l × b × h\\ & = 10 × 8 × 6\\ & = 480 ~\big(\text{cm}^{3}\big).\ _\square \end{align}\]

I made a large ice cream cone of a composite shape of a cone and a hemisphere. If the height of the cone is 10 and the diameter of both the cone and the hemisphere is 6, what is the volume of this ice cream cone? The volume of the composite figure is the sum of the volume of the cone and the volume of the hemisphere. Recall the formulas for the following two volumes: \( V_{\text{cone}} = \frac13 \pi r^2 h\) and \( V_{\text{sphere}} =\frac43 \pi r^3 \). Since the volume of a hemisphere is half the volume of a a sphere of the same radius, the total volume for this problem is \[\frac13 \pi r^2 h + \frac12 \cdot \frac43 \pi r^3. \] With height \(h =10\), and diameter \(d = 6\) or radius \(r = \frac d2 = 3 \), the total volume is \(48\pi. \ _\square \)

Find the volume of a cone having slant height \(17\text{ cm}\) and radius of the base \(15\text{ cm}\). Let \(h\) denote the height of the cone, then \[\begin{align} (\text{slant height}) &=\sqrt {h^2 + r^2}\\ 17&= \sqrt {h^2 + 15^2}\\ 289&= h^2 + 225\\ h^2&=64\\ h& = 8. \end{align}\] Since the formula for the volume of a cone is \(\dfrac {1}{3} ×\pi ×r^2×h\), the volume of the cone is \[ \frac {1}{3}×3.14× 225 × 8= 1884 ~\big(\text{cm}^{2}\big). \ _\square\]

Find the volume of the following figure which depicts a cone and an hemisphere, up to \(2\) decimal places. In this figure, the shape of the base of the cone is circular and the whole flat part of the hemisphere exactly coincides with the base of the cone (in other words, the base of the cone and the flat part of the hemisphere are the same). Use \(\pi=\frac{22}{7}.\) \[\begin{align} (\text{Volume of cone}) & = \dfrac {1}{3} \pi r^2 h\\ & = \dfrac {1 × 22 × 36 × 8}{3 × 7}\\ & = \dfrac {6336}{21} = 301.71 \\\\ (\text{Volume of hemisphere}) & = \dfrac {2}{3} \pi r^3\\ & = \dfrac {2 × 22 × 216}{3 × 7}\\ & = \dfrac {9504}{21} = 452.57 \\\\ (\text{Total volume of figure}) & = (301.71 + 452.57) \\ & = 754.28.\ _\square \end{align} \]

Try the following problems.

Find the volume (in \(\text{cm}^3\)) of a cube of side length \(5\text{ cm} \).

A spherical balloon is inflated until its volume becomes 27 times its original volume. Which of the following is true?

Bob has a pipe with a diameter of \(\frac { 6 }{ \sqrt { \pi } }\text{ cm} \) and a length of \(3\text{ m}\). How much water could be in this pipe at any one time, in \(\text{cm}^3?\)

What is the volume of the octahedron inside this \(8 \text{ in}^3\) cube?

A sector with radius \(10\text{ cm}\) and central angle \(45^\circ\) is to be made into a right circular cone. Find the volume of the cone.

\[\] Details and Assumptions:

• The arc length of the sector is equal to the circumference of the base of the cone.

Three identical tanks are shown above. The spheres in a given tank are the same size and packed wall-to-wall. If the tanks are filled to the top with water, then which tank would contain the most water?

A chocolate shop sells its products in 3 different shapes: a cylindrical bar, a spherical ball, and a cone. These 3 shapes are of the same height and radius, as shown in the picture. Which of these choices would give you the most chocolate?

\[\text{ I. A full cylindrical bar } \hspace{.4cm} \text{ or } \hspace{.45cm} \text{ II. A ball plus a cone }\]

How many cubes measuring 2 units on one side must be added to a cube measuring 8 units on one side to form a cube measuring 12 units on one side?

This section involves a deeper understanding of volume and the formulas to find the volume. Here are a couple of worked out examples followed by several "Try It Yourself" problems:

\(12\) spheres of the same size are made from melting a solid cylinder of \(16\text{ cm}\) diameter and \(2\text{ cm}\) height. Find the diameter of each sphere. Use \(\pi=\frac{22}{7}.\) The volume of the cylinder is \[\pi× r^2 × h = \frac {22×8^2×2}{7}= \frac {2816}{7}.\] Let the radius of each sphere be \(r\text{ cm}.\) Then the volume of each sphere in \(\text{cm}^3\) is \[\dfrac {4×22×r^3}{3×7} = \dfrac{88×r^3}{21}.\] Since the number of spheres is \(\frac {\text{Volume of cylinder}}{\text {Volume of 1 sphere}},\) \[\begin{align} 12 &= \dfrac{2816×21}{7×88×r^3}\\ &= \dfrac {96}{r^3}\\ r^3 &= \dfrac {96}{12}\\ &= 8\\ \Rightarrow r &= 2. \end{align}\] Therefore, the diameter of each sphere is \[2\times r = 2\times 2 = 4 ~(\text{cm}). \ _\square\]

Find the volume of a hemispherical shell whose outer radius is \(7\text{ cm}\) and inner radius is \(3\text{ cm}\), up to \(2\) decimal places. We have \[\begin{align} (\text {Volume of inner hemisphere}) & = \dfrac{1}{2} × \dfrac{4}{3} × \pi × R^3\\ & = \dfrac {1 × 4 × 22 × 27}{2 × 3 × 7}\\ & = \dfrac {396}{7}\\ & = 56.57 ~\big(\text{cm}^{3}\big) \\\\ (\text {Volume of outer hemisphere}) & = \dfrac{1}{2} × \dfrac{4}{3} × \pi × r^3\\ & = \dfrac {1 × 4 × 22 × 343}{2 × 3 × 7}\\ & = \dfrac {2156}{7}\\ & = 718.66 ~\big(\text{cm}^{3}\big) \\\\ (\text{Volume of hemispherical shell}) & = (\text{V. of outer hemisphere}) - (\text{V. of inner hemisphere})\\ & = 718.66 - 56.57 \\ & = 662.09 ~\big(\text{cm}^{3}\big).\ _\square \end{align}\]

A student did an experiment using a cone, a sphere, and a cylinder each having the same radius and height. He started with the cylinder full of liquid and then poured it into the cone until the cone was full. Then, he began pouring the remaining liquid from the cylinder into the sphere. What was the result which he observed?

There are two identical right circular cones each of height \(2\text{ cm}.\) They are placed vertically, with their apex pointing downwards, and one cone is vertically above the other. At the start, the upper cone is full of water and the lower cone is empty.

Water drips down through a hole in the apex of the upper cone into the lower cone. When the height of water in the upper cone is \(1\text{ cm},\) what is the height of water in the lower cone (in \(\text{cm}\))?

On each face of a cuboid, the sum of its perimeter and its area is written. The numbers recorded this way are 16, 24, and 31, each written on a pair of opposite sides of the cuboid. The volume of the cuboid lies between \(\text{__________}.\)

A cube rests inside a sphere such that each vertex touches the sphere. The radius of the sphere is \(6 \text{ cm}.\) Determine the volume of the cube.

If the volume of the cube can be expressed in the form of \(a\sqrt{3} \text{ cm}^{3}\), find the value of \(a\).

A sphere has volume \(x \text{ m}^3 \) and surface area \(x \text{ m}^2 \). Keeping its diameter as body diagonal, a cube is made which has volume \(a \text{ m}^3 \) and surface area \(b \text{ m}^2 \). What is the ratio \(a:b?\)

Consider a glass in the shape of an inverted truncated right cone (i.e. frustrum). The radius of the base is 4, the radius of the top is 9, and the height is 7. There is enough water in the glass such that when it is tilted the water reaches from the tip of the base to the edge of the top. The proportion of the water in the cup as a ratio of the cup's volume can be expressed as the fraction \( \frac{m}{n} \), for relatively prime integers \(m\) and \(n\). Compute \(m+n\).

The square-based pyramid A is inscribed within a cube while the tetrahedral pyramid B has its sides equal to the square's diagonal (red) as shown.

Which pyramid has more volume?

Please remember this section contains highly advanced problems of volume. Here it goes:

Cube \(ABCDEFGH\), labeled as shown above, has edge length \(1\) and is cut by a plane passing through vertex \(D\) and the midpoints \(M\) and \(N\) of \(\overline{AB}\) and \(\overline{CG}\) respectively. The plane divides the cube into two solids. The volume of the larger of the two solids can be written in the form \(\frac{p}{q}\), where \(p\) and \(q\) are relatively prime positive integers. Find \(p+q\).

If the American NFL regulation football

has a tip-to-tip length of \(11\) inches and a largest round circumference of \(22\) in the middle, then the volume of the American football is \(\text{____________}.\)

Note: The American NFL regulation football is not an ellipsoid. The long cross-section consists of two circular arcs meeting at the tips. Don't use the volume formula for an ellipsoid.

Answer is in cubic inches.

Consider a solid formed by the intersection of three orthogonal cylinders, each of diameter \( D = 10 \).

What is the volume of this solid?

Consider a tetrahedron with side lengths \(2, 3, 3, 4, 5, 5\). The largest possible volume of this tetrahedron has the form \( \frac {a \sqrt{b}}{c}\), where \(b\) is an integer that's not divisible by the square of any prime, \(a\) and \(c\) are positive, coprime integers. What is the value of \(a+b+c\)?

Let there be a solid characterized by the equation \[{ \left( \frac { x }{ a } \right) }^{ 2.5 }+{ \left( \frac { y }{ b } \right) }^{ 2.5 } + { \left( \frac { z }{ c } \right) }^{ 2.5 }<1.\]

Calculate the volume of this solid if \(a = b =2\) and \(c = 3\).

• Surface Area

Problem Loading...

Note Loading...

Set Loading...

• Maths Questions

Volume Questions

Volume questions and answers are available in an easily understandable format along with required formulas. Students can practise questions on finding the volume of various solids provided here, and verify their solutions with the available answers. This is the best way to learn about various problem-solving techniques of solids in geometry.

What is volume?

Volume is the amount of space occupied by a solid shape in a three-dimensional plane or region. Some examples of solids include cubes, cuboids, spheres, cones, cylinders, etc.

• Volume of cube = a 3 , where a is the edge of the cube.
• Volume of cuboid = lbh, where l = length, b = breadth and h = height.
• Volume of sphere = (4/3) πr 3 , where r is the radius of the sphere.
• Volume of cylinder = πr 2 h, where r is the radius of the circular bases and h is the height.
• Volume of cone = (⅓) πr 2 h, where r is the radius of the circular base and h is the height.
• Volume of hemisphere = (2/3) πr 3 , where r is the radius of the sphere.
• Volume of frustum = πh/3 (R 2 + r 2 + Rr), where ‘R’ and ‘r’ are the radii of the base and top of the frustum.
• Volume of prism = Base Area x Height.
• Volume of pyramid = ⅓ (Area of base) (Height).

Click here to learn more about volume .

Volume Questions and Answers

1. Find the volume of a cuboidal box with dimensions 11 cm × 8 cm × 13 cm.

Given, the dimensions of a cuboidal box: 11 cm × 8 cm × 13 cm

Length = l = 11 cm

Breadth = b = 8 cm

Height = h = 13 cm

As we know, volume of a cuboid = lbh

= 11 × 8 × 13

Thus, the volume of the cuboidal box is 1144 cm 3 .

2. What is the volume of a sphere of diameter 21 units?

Diameter of the sphere = 21 units

Radius of the sphere = (21/2) units

Volume of a sphere = (4/3) πr 3

= (4/3) × (22/7) × (21/2) × (21/2) × (21/2)

Therefore, the volume of the sphere is 4851 cubic units.

3. A cuboidal block of wood was cut into eight equal cubes of edges 4 cm. Find the volume of the initial block of wood.

Edge of a cubical wood = 4 cm

Volume of the cube = a 3

= 4 × 4 × 4

Volume of 8 such cubes = 8 volume of one cube

Hence, the volume of the initial cuboidal block of wood is 512 cm 3 .

4. If three solid spherical beads of radii 3 cm, 4 cm, and 5 cm, respectively, are melted into one spherical bead, then find its radius in cm.

Radii of three solid spherical beads: 3 cm, 4 cm and 5 cm

As we know, the volume of a sphere = (4/3) πr 3

Let R be the radius of the new spherical bead, which is made by melting three spherical beads.

Volume of a new spherical bead = Sum of volumes of three spherical beads

(4/3)πR 3 = (4/3) × 3 × 3 × 3 + (4/3) × 4 × 4 × 4 + (4/3) × 5 × 5 × 5

(4/3)πR 3 = (4/3)π (27 + 64 + 125)

Hence, the radius of the spherical bead is 6 cm.

5. How many bricks, each measuring 25 cm x 11.25 cm x 6 cm, will be needed to build a wall of 8 m x 6 m x 22.5 cm?

Dimensions of a brick = 25 cm x 11.25 cm x 6 cm

Dimensions of a wall = 8 m x 6 m x 22.5 cm

= 800 cm x 600 cm x 22.5 cm

Number of bricks = volume of the wall/ volume of a brick

= (800 x 600 x 22.5) / (25 x 11.25 x 6)

6. Find the depth of the cylindrical tank if its capacity is 1848 m 3 and the diameter of the base is 14 m.

Let h be the depth of the cylindrical tank.

Diameter of the base = 14 m

Radius of the circular base = r = 14/2 = 7 m

Volume of the cylindrical tank = πr2h

So, πr 2 h = 1848 m 3

(22/7) × 7 × 7 × h = 1848

h = 1848/(22 × 7)

Therefore, the depth of the cylindrical tank is 12 m.

7. What is the ratio of the volume of a cone, a sphere and a cylinder if each has the same radius and height?

Let r be the radius of the cone, sphere and cylinder.

Let h be the height of the cone and cylinder.

Also, r = h

We know that,

Volume of cone = (1/3)πr 2 h = (1/3)πr 3

Volume of sphere = (4/3)πr 3

Volume of cylinder = πr 2 h = πr 3

Volume of cone : Volume of sphere : Volume of cylinder

= (1/3)πr 2 h : (4/3)πr 3 : πr 2 h

= (1/3)πr 3 : (4/3)πr 3 : πr 3

= (1/3) : (4/3) : 1

= 1 : 4 : 3

Therefore, the required ratio is 1 : 4 : 3.

8. Find the water weight in a conical vessel that is 21 cm deep and 16 cm in diameter.

Depth of height of a conical vessel = h = 21 cm

Diameter of the circular base = 16 cm

Radius = r = 16/2 = 8 cm

Volume of a cone = (1/3)πr 2 h

= (1/3) × (22/7) × 8 × 8 × 21

= 1408 cm 3

= (1408/1000) kg

Therefore, the weight of the water in a conical vessel is 1.408 kg.

9. A vessel is in the form of a frustum of a cone. Its radius at one end and the heights are 8 cm and 14 cm, respectively. If its volume is 5676/3 cm 3 , find the radius at the other end.

Radius of one circular end = r 1 = 8 cm

Height of the frustum = h = 14 cm

Let r2 be the radius of the other circular end.

Volume of the frustum = πh/3 (r 1 2 + r 2 2 + r 1 r 2 )

= (1/3) × (22/7) × 14 × [(8) 2 + (r 2 ) 2 + 8r 2 ]

According to the given,

(1/3) × (22/7) × 14 × [(8) 2 + (r 2 ) 2 + 8r 2 ] = 5676/3 cm3

64 + r 2 2 + 8r 2 = 5676/44

r 2 2 + 8r 2 = 129 – 64

r 2 2 + 8r 2 – 65 = 0

r 2 2 + 13r 2 – 5r 2 – 65 = 0

r 2 (r 2 + 13) – 5(r 2 + 13) = 0

(r 2 – 5)(r 2 + 13) = 0

r 2 = 5, r 2 = -13

Hence, the radius of the other circular end is 5 cm.

10. If the curved surface area of a right circular cone is 10010 cm 2 and its radius is 35 cm, find the volume of the cone.

Radius of the circular base of a cone = r = 35 cm

Let h and l be the height and slant height of the right circular cone.

Also, given that the curved surface area = 10010 cm 2

πrl = 10010

(22/7) × 35 × l = 10010

l = (10010 × 7)/ (22 × 35)

As we know, l 2 = r 2 + h 2

h 2 = l 2 – r 2

= (91) 2 – (35) 2

= 8281 – 1225

Volume of the cone = (1/3) πr 2 h

= (1/3) × (22/7) × 35 × 35 × 84

Hence, the volume of the right circular cone is 107800 cm 3 .

Practice Questions on Volume

• The height of the wall is six times its width, and the length of the wall is seven times its height. If the volume of the wall is 16128 cm 3 , what is the width of the wall?
• A fish tank has a length of 45 cm, a width of 25 cm, and a depth of 10 cm. Calculate the volume of the fish tank.
• Find the volume of the cylinder with a radius of 5.4 units and a height of 16 units.
• Find the number of small cubes with edges of 10 cm that can be accommodated in a cubical box with a 1 m edge.
• The radius of a sphere is increased by 10%. Prove that the volume will be increased by 33.1% approximately.

Leave a Comment Cancel reply

Your Mobile number and Email id will not be published. Required fields are marked *

Request OTP on Voice Call

Post My Comment

Register with BYJU'S & Download Free PDFs

Register with byju's & watch live videos.

Child Login

• Kindergarten
• Number charts
• Skip Counting
• Place Value
• Number Lines
• Subtraction
• Multiplication
• Word Problems
• Comparing Numbers
• Ordering Numbers
• Odd and Even
• Prime and Composite
• Roman Numerals
• Ordinal Numbers
• In and Out Boxes
• Number System Conversions
• More Number Sense Worksheets
• Size Comparison
• Measuring Length
• Metric Unit Conversion
• Customary Unit Conversion
• Temperature
• More Measurement Worksheets
• Writing Checks
• Profit and Loss
• Simple Interest
• Compound Interest
• Tally Marks
• Mean, Median, Mode, Range
• Mean Absolute Deviation
• Stem-and-leaf Plot
• Box-and-whisker Plot
• Permutation and Combination
• Probability
• Venn Diagram
• More Statistics Worksheets
• Shapes - 2D
• Shapes - 3D
• Lines, Rays and Line Segments
• Points, Lines and Planes
• Transformation
• Quadrilateral
• Ordered Pairs
• Midpoint Formula
• Distance Formula
• Parallel, Perpendicular and Intersecting Lines
• Scale Factor
• Surface Area
• Pythagorean Theorem
• More Geometry Worksheets
• Converting between Fractions and Decimals
• Significant Figures
• Convert between Fractions, Decimals, and Percents
• Proportions
• Direct and Inverse Variation
• Order of Operations
• Squaring Numbers
• Square Roots
• Scientific Notations
• Speed, Distance, and Time
• Absolute Value
• More Pre-Algebra Worksheets
• Translating Algebraic Phrases
• Evaluating Algebraic Expressions
• Simplifying Algebraic Expressions
• Algebraic Identities
• Quadratic Equations
• Systems of Equations
• Polynomials
• Inequalities
• Sequence and Series
• Complex Numbers
• More Algebra Worksheets
• Trigonometry
• Math Workbooks
• English Language Arts
• Summer Review Packets
• Social Studies
• Holidays and Events
• Worksheets >
• Geometry >

Volume Worksheets

This humongous collection of printable volume worksheets is sure to walk middle and high school students step-by-step through a variety of exercises beginning with counting cubes, moving on to finding the volume of solid shapes such as cubes, cones, rectangular and triangular prisms and pyramids, cylinders, spheres and hemispheres, L-blocks, and mixed shapes. Brimming with learning and backed by application the PDFs offer varied levels of difficulty.

List of Volume Worksheets

Counting Cubes

• Volume of Cubes
• Volume of Rectangular Prisms
• Volume of Triangular Prisms

Volume of Mixed Prisms

• Volume of Cones
• Volume of Cylinders

Volume of Spheres and Hemispheres

• Volume of Rectangular Pyramids
• Volume of Triangular Pyramids

Volume of Mixed Pyramids

Volume of Mixed Shapes

Volume of Composite Shapes

Explore the Volume Worksheets in Detail

Work on the skill of finding volume with this batch of counting cubes worksheets. Count unit cubes to determine the volume of rectangular prisms and solid blocks, draw prisms on isometric dot paper and much more.

Volume of a Cube

Augment practice with this unit of pdf worksheets on finding the volume of a cube comprising problems presented as shapes and in the word format with side length measures involving integers, decimals and fractions.

Volume of a Rectangular Prism

This batch of volume worksheets provides a great way to learn and perfect skills in finding the volume of rectangular prisms with dimensions expressed in varied forms, find the volume of L-blocks, missing measure and more.

Volume of a Triangular Prism

Encourage students to work out the entire collection of printable worksheets on computing the volume of triangular prism using the area of the cross-section or the base and leg measures and practice unit conversions too.

Navigate through this collection of volume of mixed prism worksheets featuring triangular, rectangular, trapezoidal and polygonal prisms. Bolster practice with easy and moderate levels classified based on the number range used.

Volume of a Cone

Motivate learners to use the volume of a cone formula efficiently in the easy level, find the radius in the moderate level and convert units in the difficult level, solve for volume using slant height, and find the volume of a conical frustum too.

Volume of a Cylinder

Access our volume of a cylinder worksheets to practice finding the radius from diameter, finding the volume of cylinders with parameters in integers and decimals, find the missing parameters, solve word problems and more!

Take the hassle out of finding the volume of spheres and hemispheres with this compilation of pdf worksheets. Gain immense practice with a wide range of exercises involving integers and decimals.

Volume of a Rectangular Pyramid

This exercise is bound to help learners work on the skill of finding the volume of rectangular pyramids with dimensions expressed as integers, decimals and fractions in easy and moderate levels.

Volume of a Triangular Pyramid

Help children further their practice with this bundle of pdf worksheets on determining the volume of triangular pyramids using the measures of the base area or height and base. The problems are offered as 3D shapes and in word format in varied levels of difficulty.

Gain ample practice in finding the volume of pyramids with triangular, rectangular and polygonal base faces presented in two levels of difficulty. Apply relevant formulas to find the volume using the base area or the other dimensions provided.

Upscale practice with an enormous collection of printable worksheets on finding the volume of solid shapes like prisms, cylinders, cones, pyramids and revision exercises to revisit concepts with ease.

Learn to find the volume of composite shapes that are a combination of two or more solid 3D shapes. Begin with counting squares, find the volume of L -blocks, and compound shapes by adding or subtracting volumes of decomposed shapes.

Sample Worksheets

Become a Member

Membership Information

Printing Help

How to Use Online Worksheets

How to Use Printable Worksheets

Privacy Policy

Terms of Use

Copyright © 2024 - Math Worksheets 4 Kids

Volume Worksheets

• Kindergarten

PROBLEMS ON VOLUME

To find volume of the shapes, we will be using the formulas given below.

Volume of sphere  =   (4/3) π r 3

Volume of hemisphere  =   (2/3) π r 3

Volume of cone  =   (1/3) π r 2 h

Volume of cylinder  =   π r 2 h

Problem 1 :

A steel bar is 2.2 m long and has a diameter of 5 cm. Find the volume of the bar in cm 3 .

Length of steel bar  =  2.2 m  (or)  220 cm

Radius  =  5/2  ==>  2.5 cm

Volume of steel bar  =   π r 2 h

=  (3.14)  (2.5) 2 (220)

=  4317.5 cm 3

Problem 2 :

A stainless steel wine vat is cylindrical with base diameter 1.8 m and height 6 m. How much wine does it hold if it is 90% full?

Radius  =  1.8 m, height  =  6 m

Volume of steel bar  =  90% of  π r 2 h

=  0.90 x 3.14 x (1.8) 2 x 6

=  54.93 m 3

Problem 3 :

A box has a square base and its height is 12 cm. If the volume of the box is 867 cm 3 , find its length.

Let base length of the square as x.

Volume of box  =  867 cm 3

Area of square base x height  =  867

x 2 x 12  =  867

x 2   =  867/12

x 2   =  72.25

x  =  8.5 cm

Problem 4 :

15.4 mm of a rain falls on a rectangular shed roof of length 12 m and width 5.5 m. All of the water goes into a cylindrical tank of base diameter 4.35 m. By how much does the water level in the tank rise in mm ?

Measures of rectangular shed :

Length  =  12 m  =  12000 mm

width  =  5.5 m  =  5500  mm

height  =  15.4 mm

Radius  =  4.35/2  =  2.175 m

=  2175 mm

Volume of water in rectangular tank  =  Volume of water in cylindrical tank

length x width x height  =  π r 2 h

12000 x 5500 x 15.4  =  3.14 x ( 2.175) 2 x h

h  =  ( 12000 x 5500 x 15.4)/3.14 x (2175) 2

h  =  68.42 mm

Problem 5 :

Find the volume of the figure shown below.

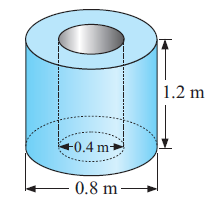
Volume  =  Base area x height

Base area  =  Area of large circle - Area of small circle

Let R and r be radius of large and small circles respectively.

R  =  0.8/2, r  =  0.4/2

R  =  0.4 m and r  =  0.2 m

Area of base  =  πR 2 -  πr 2

=   π(0.4 2 - 0.2 2 )

=  3.14(0.12)

Area of base  =  0.3768 m 2

Height  =  1.2 m

Volume  =  0.3768 x 1.2

=  0.45216 m 3

Problem 6 :

Find the volume of the figure given below.

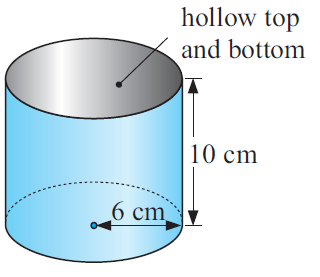
Volume of cylinder  =   πr 2 h

radius  =  6 cm and height  =  10 cm

=   π(6) 2 (10)

=  3.14(36)(10)

Volume of cylinder  =  1130.4 cm 3

Problem 7 :

Tom has just had a load of sand delivered. A pile of sand is in the shape of a cone of radius 1.6 m and height 1.2 m. Find the volume of sand Tom has had delivered.

Volume of sand to be delivered  =  (1/3)  πr 2 h

radius  =  1.6 m and height  =  1.2 m

=  (1/3)  π(1.6) 2 (1.2)

=  (1/3)x3.14x (1.6) 2 (1.2)

=  3.19 m 3

Volume of sand delivered is  3.19 m 3 .

Apart from the stuff given above ,    if you need any other stuff in math, please use our google custom search here.

Kindly mail your feedback to   [email protected]

We always appreciate your feedback.

© All rights reserved. onlinemath4all.com

• Sat Math Practice
• SAT Math Worksheets
• PEMDAS Rule
• BODMAS rule
• GEMDAS Order of Operations
• Math Calculators
• Transformations of Functions
• Order of rotational symmetry
• Lines of symmetry
• Compound Angles
• Quantitative Aptitude Tricks
• Trigonometric ratio table
• Word Problems
• Times Table Shortcuts
• 10th CBSE solution
• PSAT Math Preparation
• Privacy Policy
• Laws of Exponents

Recent Articles

SAT Math Resources (Videos, Concepts, Worksheets and More)

Dec 23, 24 03:47 AM

Digital SAT Math Problems and Solutions (Part - 91)

Dec 23, 24 03:40 AM

Digital SAT Math Problems and Solutions (Part - 90)

Dec 21, 24 02:19 AM

High Impact Tutoring Built By Math Experts

Personalized standards-aligned one-on-one math tutoring for schools and districts

In order to access this I need to be confident with:

Area of polygons

Here you will learn about volume, including what it is and how to calculate it to solve problems.

Students will first learn about volume as part of measurement and data in the 5 th grade, and continue to expand on their knowledge in geometry in the 6 th and 7 th grade.

What is volume?

Volume is a measurement of the amount of space there is within 3D shapes.

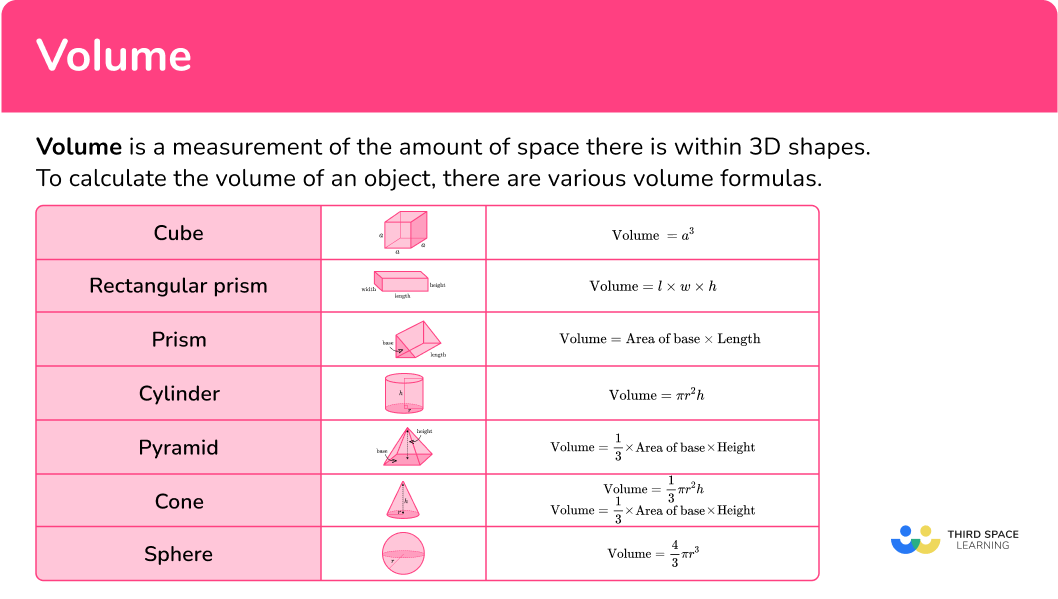
To calculate the volume of an object, there are various volume formulas.

Step-by-step guide: Volume formula

Let’s look at each type of 3 -dimensional shape.

A prism is made up of 2 congruent bases, connected by lateral faces. For right prisms, the lateral sides are always rectangles.

For example,

Imagine filling this triangle prism fully with water. The total amount of water inside the prism would represent the volume of the prism in cubic units.

\text { Volume of prism }=\text { Area of the base } \times \text { height }

To calculate the volume of any prism, calculate the area of the base and times it by the height.

Step-by-step guide: Volume of a prism

The volume of a rectangular prism can be found by counting the cubic units with the prism.

This rectangular prism is made from 24 unit cubes – each side is 1 \, cm. That means the space within the rectangular prism, or the volume, is 24 \, cm^3.

You can prove that the volume is 24 \, cm^3 , by counting the total cubes, or by using the formula.

\begin{aligned}\text { Volume of a rectangular prism } & =\text { length } \times \text { width } \times \text { height } \\\\ & =6 \mathrm{~cm} \times 2 \mathrm{~cm} \times 2 \mathrm{~cm} \\\\ & =24 \mathrm{~cm}^3\end{aligned}

Step-by-step guide: Volume of a rectangular prism

To find the volume of a cube, use the volume of a cube formula. The formula is similar to l \times w \times h , but since all sides of a cube are the same length, you can just multiply one side length, a , three times: \text {Volume }=a^{3} .

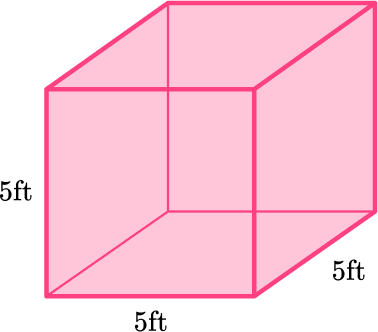
The volume of this cube is:

\begin{aligned}& \text { volume }=a^3 \\\\ & \text { volume }=5^3 \\\\ & \text { volume }=125 \mathrm{~ft}^3\end{aligned}

Step-by-step guide: Volume of a cube

Step-by-step guide: Volume of a pyramid

[FREE] Volume Worksheet (Grade 6 to 8)

Use this quiz to check your grade 6 to 8 students’ understanding of volume. 10+ questions with answers covering a range of 6th, 7th and 8th grade volume topics to identify areas of strength and support!

Common Core State Standards

How does this relate to 5 th, 6 th and 7 th grade math?

• Grade 5: Measurement and Data (5.MD.C.5b) Apply the formulas V=l \times w \times h and V=b \times h for rectangular prisms to find volumes of right rectangular prisms with whole number edge lengths in the context of solving real world and mathematical problems.
• Grade 6: Geometry (6.G.A.2) Find the volume of a right rectangular prism with fractional edge lengths by packing it with unit cubes of the appropriate unit fraction edge lengths, and show that the volume is the same as would be found by multiplying the edge lengths of the prism. Apply the formulas V=l \times w \times h and V=b \times h to find volumes of right rectangular prisms with fractional edge lengths in the context of solving real-world and mathematical problems.
• Grade 7: Geometry (7.G.B.6) Solve real-world and mathematical problems involving area, volume and surface area of two- and three-dimensional objects composed of triangles, quadrilaterals, polygons, cubes, and right prisms.

How to calculate volume

In order to calculate volume:

Write down the formula.

Substitute the values into the formula.

Calculate the volume of the shape.

Write the answer, including the units.

Volume examples

Example 1: volume of a triangular prism.

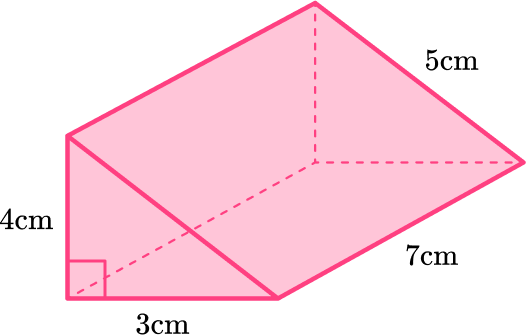
Calculate the volume of the triangular prism:

2 Substitute the values into the formula.

A triangular prism has two congruent triangular bases connected by lateral faces – so the base is the triangle. The height of the prism is 7 \, cm.

\begin{aligned}\text { Volume of prism }&=\text { Area of the base (triangle }) \, \times \, \text { height of prism } \\\\ & =\cfrac{1}{2} \times 3 \times 4 \times \, 7 \\\\ &\end{aligned}

3 Calculate the volume of the shape.

\begin{aligned}\text { Volume } & =\cfrac{1}{2} \, \times 3 \, \times 4 \, \times 7 \\\\ & =6 \, \times \, 7 \\\\ & =42\end{aligned}

4 Write the answer, including the units.

The measurements on this triangular prism are in centimeters, so the volume is measured in cubic centimeters.

\text { Volume }=42 \mathrm{~cm}^3

Example 2: volume of a cube – fractions

Calculate the volume of the cube:

\text { Volume of a cube }=a^3

A cube has a side length of 3 \cfrac{4}{5} , so a=3 \cfrac{4}{5} .

\begin{aligned} \text { Volume of a cube } & =a^3 \\\\ & =\left(3 \cfrac{4}{5}\right)^3 \\\\ \end{aligned}

\begin{aligned} \text { Volume } & =3 \cfrac{4}{5} \, \times \, 3 \cfrac{4}{5} \, \times \, 3 \cfrac{4}{5} \\\\ & =14 \cfrac{11}{25} \, \times \, 3 \cfrac{4}{5} \\\\ & =\cfrac{361}{25} \, \times \, \cfrac{19}{5} \\\\ & =\cfrac{6,859}{125} \\\\ & =54 \cfrac{109}{125}\end{aligned}

The measurements on this cube are in meters, so the volume is measured in cubic meters.

\text { Volume }=54 \cfrac{109}{125} \mathrm{~m}^3

Example 3: volume of a pentagonal prism

Calculate the volume of the prism:

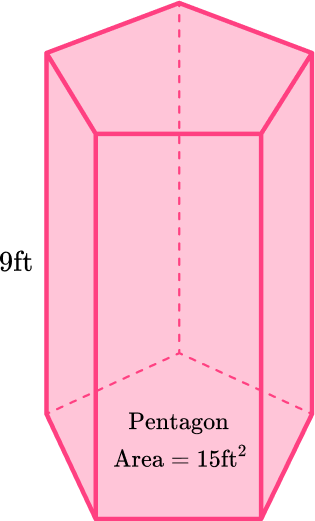
A pentagonal prism has two congruent pentagonal bases connected by lateral faces – so the base is a pentagon. The area of the pentagon is 15 \, ft^2. The height of the prism is 9 \, ft .

\begin{aligned} \text { Volume of prism } & =\text { Area of the base (pentagon}) \, \times \, \text {height of prism } \\\\ & = 15 \, \times \, 9\\\\ \end{aligned}

\begin{aligned}\text {Volume of prism } & =15 \, \times \, 9 \\\\ & =135\end{aligned}

The measurements on this prism are in feet, so the volume is measured in cubic feet.

\text { Volume }=135 \mathrm{ft}^3

Example 4: missing dimension

The volume of the rectangular prism is 108 \mathrm{~cm}^3.

Calculate the value of x .

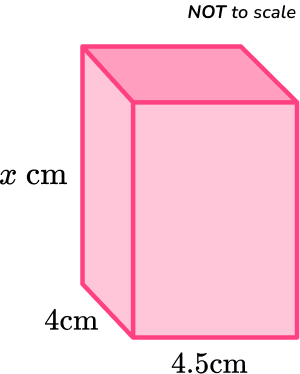
The 3D shape is a rectangular prism.

The formula you need to use is \text{Volume}=l\times w\times h.

The length (l), the width (w) and the height (h) of the rectangular prism are interchangeable, so it doesn’t matter which dimension l or w or h.

The values you need to substitute into the formula are \text {Volume}=108, l=4 and w=4.5.

For the height (h) , you can use x .

\begin{aligned}\text { Volume } &=l \, \times \, w \, \times \, h \\\\ \ 108 &=4 \, \times \, 4.5 \, \times \, x \\\\ \ 108 &=18 \, \times \, x\end{aligned}

In this case, you already know the volume. You divide the volume by the area of the base to find the missing height.

x=108 \div 18=6.

The dimensions of the rectangular prism were given in centimeters, and the volume was given in cubic centimeters (cm^3).

Since x is a dimension of the rectangular prism, it is recorded in just units, not units cubed.

Example 5: missing dimension

The volume of the square pyramid is 32 \text { inches }^3.

Calculate the height of the pyramid.

The 3D shape is a pyramid. The formula you need to use is:

\text{Volume}=\cfrac{1}{3} \, \times \, \text{Area of Base} \times \text{Height}

First you need to calculate the area of the square base, 64=4 \times 4=16.

The values you need to substitute into the formula are \text{volume}=32 and \text{area of base}=16.

For the height, you can use h .

\begin{aligned}\text{Volume} &=\cfrac{1}{3} \, \times \, \text{Area of base} \, \times \, \text{Height}\\\\ 32 & =\cfrac{1}{3} \, \times \, 16 \times \, h \\\\ 32 &=5 \cfrac{1}{3} \, \times \, h\end{aligned}

\begin{aligned}h & =32 \div 5 \cfrac{1}{3} \\\\ & =32 \div \cfrac{16}{3} \\\\ & =\cfrac{32}{1} \times \cfrac{3}{16} \\\\ & =\cfrac{96}{16} \\\\ & =6\end{aligned}

The dimensions of the pyramid were given in inches and the volume was given in cubic inches (inches^3).

Since h is a dimension of the square pyramid, it is recorded in just units, not units cubed.

h=6 \, inches

Example 6: volume of a compound shape

Calculate the volume of the compound 3D shape.

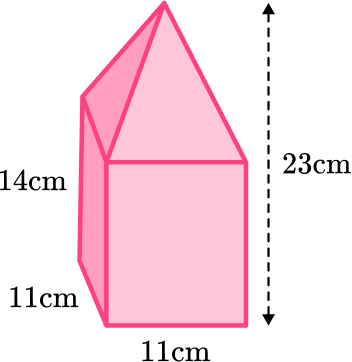
The 3D shape is made from a rectangular prism and a pyramid. Find the volume of each part and then add the volumes together. Use the formulas:

The volume of the shape is:

\text { Total Volume }=1,694+363=2,057.

The dimensions of the compound 3D shape are in centimeters, so the volume is in cubic centimeters (cm^3).

V=2,057 \, cm^3

Teaching tips for volume

• Have students create or identify examples of cubic units to be displayed in the classroom. For example, most ones cubes included in math manipulative kits are 1 centimeter cubed. Students can take 12 rulers and tape them together to form a cubic foot, 12 yard sticks to form a cubic yard or 12 meter sticks to form a cubic meter. Activities like this give students a visual understanding of how big or small different cubic units are and can also lead to discussions about why labeling cubic units is important.
• Incorporate interactive demonstrations to show what volume is and why the formulas work. For example, using the volume of a container. Start by filling the container with water and asking students to estimate the volume of water within it. Then measure the volume of water in mL and use the dimensions of the container to calculate the volume in centimeters cubed. Use the findings or student thinking to guide a conversation about what this activity shows us about volume.
• Uses quizzes, worksheets, or project assignments to provide timely and constructive feedback to address any misconceptions or errors when calculating volume or using the volume formulas.

Easy mistakes to make

• Using the volume formula with different units All measurements of a shape being used in the volume formula need to be in the same units before calculating the volume.
• Confusing the formulas for calculating volume There are many different formulas used for volume, and it is easy to get them confused. Always think about whether or not the formula you are using makes sense. For example, The formula for the volume of a triangular prism is \cfrac{1}{2} \times b \times h \times p r i s m \text { height }. Within the formula is the area of a triangle (\cfrac{1}{2} \times b \times h), which is the base and then that base area times the height. If you wanted to find the area of a rectangular prism, you should recognize that there is no triangle, so instead the area of the base would need to be l \times w . Step-by-step guide : Volume of a triangular prism

Practice volume questions

1. Calculate the volume of this pyramid.

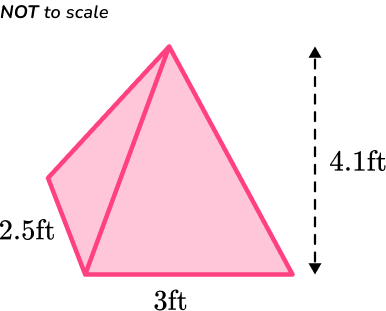
The volume formula to calculate the volume of the pyramid is:

\text{Volume} =\cfrac{1}{3}\times \text{Area of base}\times \text{Height}.

You need to find the area of the base of the pyramid.

A=2.5 \times 3=7.5

\begin{aligned} \text{ Volume }&=\cfrac{1}{3} \times \text { Area of base } \times \text { Height } \\\\ & =\cfrac{1}{3} \times 7.5 \times 4.1 \\\\ & =10.25\end{aligned}

The volume of the pyramid is 10.25 \text { inches}^3.

2. The volume of this rectangular prism is 780 \mathrm{~mm}^3. Calculate the length of the missing side.

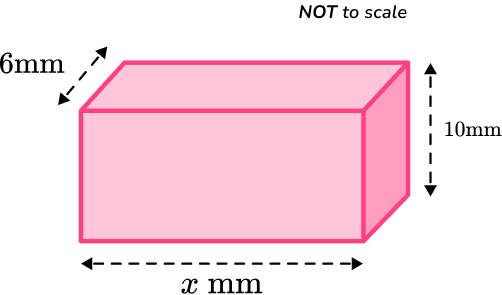
The volume formula to calculate the volume of the rectangular prism is  \text{Volume} =l\times w\times h.

You need to substitute the values given, using x for the unknown length, into the volume formula.

\begin{aligned}\text { Volume }&=l \times w \times h \\\\ 780 &=x \times 6 \times 10 \\\\ 780 &=x \times 60\end{aligned}

The missing length is x=780 \div 60=13.

The missing length of the rectangular prism is 13 \, mm.

3. Calculate the volume of this triangular prism.

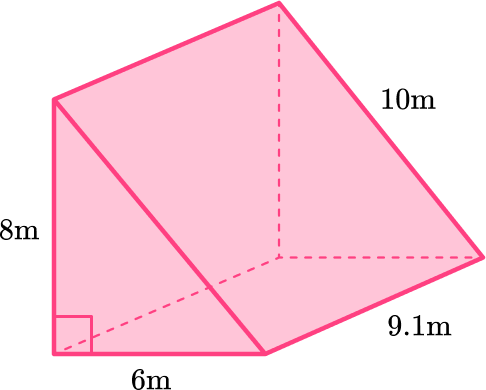
A triangular prism has two congruent triangular bases connected by lateral faces – so the base is the triangle.

\begin{aligned}\text { Area of triangle } &=\cfrac{1}{2} \times b \times h \\\\ &=\cfrac{1}{2} \times 6 \times 8 \\\\ &=24\end{aligned}

The area of the triangle is 24 \mathrm{~m}^2.

The height of the prism is 9.1 \, m.

\begin{aligned}\text { Volume of prism } & =\text { Area of the base } \times \text { height } \\\\ & =24 \times 9.1 \\\\ & =218.4\end{aligned}

The measurements on this triangular prism are in meters, so the volume is measured in cubic meters.

\text { Volume }=218.4 \mathrm{~m}^3

4. Calculate the volume of this hexagonal prism.

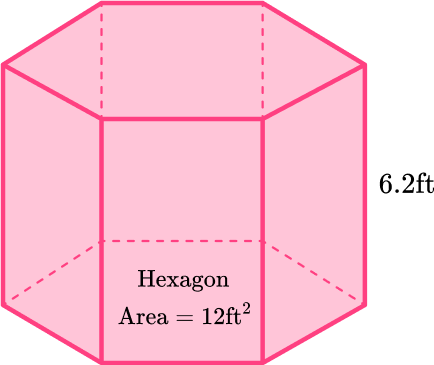
A hexagonal prism has two congruent hexagonal bases connected by lateral faces – so the base is a hexagon. The area of the hexagon is 12 \mathrm{ft}^2.

The height of the prism is 6.2 \, ft.

\begin{aligned}\text { Volume of prism } & =\text { Area of the base } \times \text { height } \\\\ & =12 \times 6.2 \\\\ & =74.4\end{aligned}

\text { Volume }=74.4 \mathrm{ft}^3

5. Calculate the volume of this triangular prism.

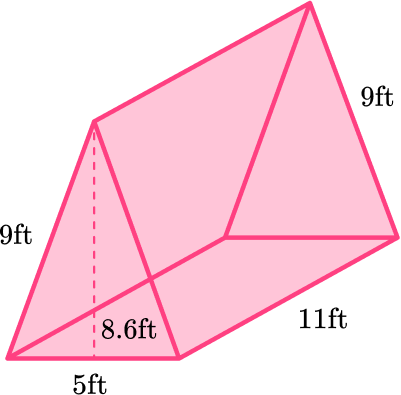
\begin{aligned}\text { Area of triangle } & =\cfrac{1}{2} \times b \times h \\\\ & =\cfrac{1}{2} \times 5 \times 8.6 \\\\ & =21.5\end{aligned}

The area of the triangle is 21.5 \mathrm{ft}^2.

The height of the prism is 11 \, ft.

\begin{aligned}\text { Volume of prism } & =\text { Area of the base } \times \text { height } \\\\ &=21.5 \times 11 \\\\ & =236.5\end{aligned}

The measurements on this triangular prism are in feet, so the volume is measured in cubic feet.

\text { Volume }=236.5 \mathrm{ft}^3

6. Calculate the volume of the shape below.

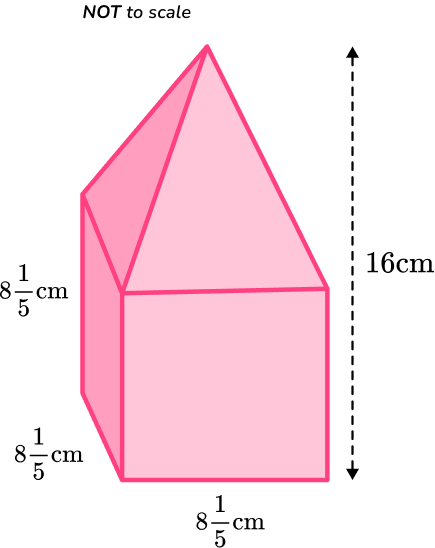
The volume of the rectangular prism is:

\begin{aligned} \text { Volume }&=l \times w \times h \\\\ & =8 \, \cfrac{1}{5} \, \times 8 \, \cfrac{1}{5} \, \times 8 \, \cfrac{1}{5} \\\\ & =\cfrac{41}{5} \, \times \cfrac{41}{5} \, \times \cfrac{41}{5} \\\\ & =\cfrac{68,921}{125} \\\\ & =551 \, \cfrac{46}{125}\end{aligned}

The height of the pyramid is 16-8 \, \cfrac{1}{5} \, =7 \, \cfrac{4}{5}.

The volume of the pyramid is

\begin{aligned}\text { Volume } &=\cfrac{1}{3} \, \times \text { Area of base } \times \text { Height } \\\\ & =\cfrac{1}{3} \, \times 8 \, \cfrac{1}{5} \times 8 \, \cfrac{1}{5} \, \times 7 \, \cfrac{4}{5} \\\\ & =\cfrac{1}{3} \, \times \cfrac{41}{5} \, \times \cfrac{41}{5} \, \times \cfrac{39}{5} \\\\ & =\cfrac{65,559}{375} \\\\ & =174 \, \cfrac{309}{375}\end{aligned}

The total volume can be found by adding the two volumes together.

\begin{aligned}\text { Total Volume } &=551 \, \cfrac{46}{125}+174 \, \cfrac{309}{375} \\\\ & =551 \, \cfrac{138}{375}+174 \, \cfrac{309}{375} \\\\ & =725 \, \cfrac{447}{375} \\\\ & =726 \, \cfrac{72}{375}\mathrm{~cm}^3\end{aligned}

Volume FAQs

The volume of a cuboid is found by multiplying the length, width and height. It is the same as a rectangular prism, because they are the same shape – they are synonyms.

Both of these shapes have a circular base, so you need to know how to find the area of a circle. Once you know how to find the area of a circle, you can use the following formulas to calculate the volume of each: cone is \cfrac{1}{3} \pi r^2 h and cylinder is \pi r^2 h. Step-by-step guide : Volume of a cylinder Step-by-step guide : Volume of a cone

Area is a measurement of two-dimensional space and volume is a measurement of three-dimensional space inside of three-dimensional shapes.

The metric system is a system of measurements that include millimeter, centimeter, meter, kilometer and more. It is a base 10 measurement system that is used throughout the world.

A volume unit is always cubed, since it involves three dimensions – length, width and height. There are many units used to measure volume. For example, cm³ and ft³. The volume of liquids inside of an object is referred to as capacity and is often expressed in units like liters or gallons.

The next lessons are

• Surface area
• Pythagorean theorem
• Trigonometry
• Volume of a hemisphere
• Volume of a sphere
• Volume of square pyramid

Still stuck?

At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.

Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .

[FREE] Common Core Practice Tests (3rd to 8th Grade)

Prepare for math tests in your state with these 3rd Grade to 8th Grade practice assessments for Common Core and state equivalents.

Get your 6 multiple choice practice tests with detailed answers to support test prep, created by US math teachers for US math teachers!

Privacy Overview