data analysis case study in r

• Case Study: Exploratory Data Analysis in R
• by Daniel Pinedo
• Last updated about 4 years ago
• Hide Comments (–) Share Hide Toolbars

Twitter Facebook Google+

Or copy & paste this link into an email or IM:

R news and tutorials contributed by hundreds of R bloggers

A data science case study in r.

Posted on March 13, 2017 by Robert Grünwald in R bloggers | 0 Comments

[social4i size="small" align="align-left"] --> [This article was first published on R-Programming – Statistik Service , and kindly contributed to R-bloggers ]. (You can report issue about the content on this page here ) Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.

Demanding data science projects are becoming more and more relevant, and the conventional evaluation procedures are often no longer sufficient. For this reason, there is a growing need for tailor-made solutions, which are individually tailored to the project’s goal, which is often implemented by  R programming . T o provide our readers with support in their own R programming, we have carried out an example evaluation which demonstrates several application possibilities of the R programming.

Data Science Projects

Approaching your first data science project can be a daunting task. Luckily, there are rough step-by-step outlines and heuristics than can help you on your way to becoming a data ninja. In this article, we review some of these guidelines and apply them to an example project in R.

For our analysis and the R programming, we will make use of the following R packages:

Anatomy of a Data Science project

A basic data science project consists of the following six steps:

• State the problem you are trying to solve. It has to be an unambiguous question that can be answered with data and a statistical or machine learning model. At least, specify: What is being observed? What has to be predicted?
• Collect the data, then clean and prepare it. This is commonly the most time-consuming task, but it has to be done in order to fit a prediction model with the data.
• Explore the data. Get to know its properties and quirks. Check numerical summaries of your metric variables, tables of the categorical data, and plot univariate and multivariate representations of your variables. By this, you also get an overview of the quality of the data and can find outliers.
• Check if any variables may need to be transformed. Most commonly, this is a logarithmic transformation of skewed measurements such as concentrations or times. Also, some variables might have to be split up into two or more variables.
• Choose a model and train it on the data. If you have more than one candidate model, apply each and evaluate their goodness-of-fit using independent data that was not used for training the model.
• Use the best model to make your final predictions.

We apply the principles on an example data set that was used in the ASA’s 2009 Data expo . The given data are around 120 million commercial and domestic flights within the USA between 1987 and 2008. Measured variables include departure and arrival airport, airline, and scheduled and actual departure and arrival times.

We will focus on the 2008 subset of this data. Because even this is a 600MB subset, it makes sense to start a first analysis on a random sample of this data to be able to quickly explore and develop your code, and then, periodically verify on the real data set that your results are still valid on the complete data.

The following commands read in our subset data and display the first three observations:

Fortunately, the ASA provides a code book with descriptions of each variable here . For example, we now know that for the Variable DayOfWeek, a 1 denotes Monday, a 2 is Tuesday, and so on.

The problem

With this data, it is possible to answer many interesting questions. Examples include:

Do planes with a delayed departure fly with a faster average speed to make up for the delay?

How does the delay of arriving flights vary during the day are planes more delayed on weekends.

• How has the market share of different airlines shifted over these 20 years?
• Are there specific planes that tend to have longer delays? What characterizes them? Maybe the age, or the manufacturer?

Additionally to these concrete questions, the possibilities for explorative, sandbox-style data analysis are nearly limitless.

Here, we will focus on the first two boldened questions.

Data cleaning

You should always check out the amount of missing values in your data. For this, we write an sapply-loop over each column in the flights data and report the percentage of missing values:

We see that most variables have at most a negligible amount of missing values. However, the last five variables, starting at the CarrierDelay, show almost 80% missing values. This is usually an alarmingly high amount of missing data that would suggest dropping this variable from the analysis altogether, since not even a sophisticated imputing procedure can help here. But, as further inspection shows, these variables only apply for delayed flights, i.e. a positive value in the ArrDelay column.

When selecting only the arrival delay and the five sub-categories of delays, we see that they add up to the total arrival delay. For our analysis here, we are not interested in the delay reason, but view only the total ArrDelay as our outcome of interest.

The pipe operator %>%, by the way, is a nice feature of the magrittr package (also implemented in dplyr) that resembles the UNIX-style pipe. The following two lines mean and do exactly the same thing, but the second version is much easier to read:

The pipe operator thus takes the output of the left expression, and makes it the first argument of the right expression.

We have surprisingly clean data where not much has to be done before proceeding to feature engineering.

Explorative analyses

Our main variables of interest are:

• The date, which conveniently is already split up in the columns Year, Month, and DayOfMonth, and even contains the weekday in DayOfWeek. This is rarely the case, you mostly get a single column with a name like date and entries such as „2016-06-24“. In that case, the R package lubridate provides helpful functions to efficiently work with and manipulate these dates.
• CRSDepTime, the scheduled departure time. This will indicate the time of day for our analysis of when flights tend to have higher delays.
• ArrDelay, the delay in minutes at arrival. We use this variable (rather than the delay at departure) for the outcome in our first analysis, since the arrival delay is what has the impact on our day.
• For our second question of whether planes with delayed departure fly faster, we need DepDelay, the delay in minutes at departure, as well as a measure of average speed while flying. This variable is not available, but we can compute it from the available variables Distance and AirTime. We will do that in the next section, „Feature Engineering“.

Let’s have an exploratory look at all our variables of interest.

Flight date

Since these are exploratory analyses that you usually won’t show anyone else, spending time on pretty graphics does not make sense here. For quick overviews, I mostly use the standard graphics functions from R, without much decoration in terms of titles, colors, and such.

Since we subsetted the data beforehand, it makes sense that all our flights are from 2008. We also see no big changes between the months. There is a slight drop after August, but the remaining changes can be explained by the number of days in a month.

The day of the month shows no influence on the amount of flights, as expected. The fact that the 31st has around half the flights of all other days is also obvious.

When plotting flights per weekday, however, we see that Saturday is the most quiet day of the week, with Sunday being the second most relaxed day. Between the remaining weekdays, there is little variation.

Departure Time

A histogram of the departure time shows that the number of flights is relatively constant from 6am to around 8pm and dropping off heavily before and after that.

Arrival and departure delay

Both arrival and departure delay show a very asymmetric, right-skewed distribution. We should keep this in mind and think about a logarithmic transformation or some other method of acknowledging this fact later.

The structure of the third plot of departure vs. arrival delay suggests that flights that start with a delay usually don’t compensate that delay during the flight. The arrival delay is almost always at least as large as the departure delay.

To get a first overview for our question of how the departure time influences the average delay, we can also plot the departure time against the arrival delay:

Aha! Something looks weird here. There seem to be periods of times with no flights at all. To see what is going on here, look at how the departure time is coded in the data:

A departure of 2:55pm is written as an integer 1455. This explains why the values from 1460 to 1499 are impossible. In the feature engineering step, we will have to recode this variable in a meaningful way to be able to model it correctly.

Distance and AirTime

Plotting the distance against the time needed, we see a linear relationship as expected, with one large outlier. This one point denotes a flight of 2762 miles and an air time of 823 minutes, suggesting an average speed of 201mph. I doubt planes can fly at this speed, so we should maybe remove this observation.

Feature Engineering

Feature engineering describes the manipulation of your data set to create variables that a learning algorithm can work with. Often, this consists of transforming a variable (through e.g. a logarithm), or extracting specific information from a variable (e.g. the year from a date string), or converting something like the ZIP code to a

For our data, we have the following tasks:

• Convert the weekday into a factor variable so it doesn’t get interpreted linearly.
• Create a log-transformed version of the arrival and departure delay.
• Transform the departure time so that it can be used in a model.
• Create the average speed from the distance and air time variables.

Converting the weekday into a factor is important because otherwise, it would be interpreted as a metric variable, which would result in a linear effect. We want the weekdays to be categories, however, and so we create a factor with nice labels:

log-transform delay times

When looking at the delays, we note that there are a lot of negative values in the data. These denote flights that left or arrived earlier than scheduled. To allow a log-transformation, we set all negative values to zero, which we interpret as „on time“:

Now, since there are zeros in these variables, we create the variables log(1+ArrDelay) and log(1+DepDelay):

Transform the departure time

The departure time is coded in the format hhmm, which is not helpful for modelling, since we need equal distances between equal durations of time. This way, the distance between 10:10pm and 10:20pm would be 10, but the distance between 10:50pm and 11:00pm, the same 10 minutes, would be 50.

For the departure time, we therefore need to convert the time format. We will use a decimal format, so that 11:00am becomes 11, 11:15am becomes 11.25, and 11:45 becomes 11.75.

The mathematical rule to transform the „old“ time in hhmm-format into a decimal format is:

Here, the first part of the sum generates the hours, and the second part takes the remainder when dividing by 100 (i.e., the last two digits), and divides them by 60 to transform the minutes into a fraction of one hour.

Let’s implement that in R:

Of course, you should always verify that your code did what you intended by checking the results.

Create average speed

The average flight speed is not available in the data – we have to compute it from the distance and the air time:

We have a few outliers with very high, implausible average speeds. Domain knowledge or a quick Google search can tell us that speeds of more than 800mph are not maintainable with current passenger planes. Thus, we will remove these flights from the data:

Choosing an appropriate Method

For building an actual model with your data, you have the choice between two worlds, statistical modelling and machine learning.

Broadly speaking, statistical models focus more on quantifying and interpreting the relationships between input variables and the outcome. This is the case in situations such as clinical studies, where the main goal is to describe the effect of a new medication.

Machine learning methods on the other hand focus on achieving a high accuracy in prediction, sometimes sacrificing interpretability. This results in what is called „black box“ algorithms, which are good at predicting the outcome, but it’s hard to see how a model computes a prediction for the outcome. A classic example for a question where machine learning is the appropriate answer is the product recommendation algorithm on online shopping websites.

For our questions, we are interested in the effects of certain input variables (speed and time of day / week). Thus we will make use of statistical models, namely a linear model and a generalized additive model.

To answer our first question, we first plot the variables of interest to get a first impression of the relationship. Since these plots will likely make it to the final report or at least a presentation to your supervisors, it now makes sense to spend a little time on generating a pretty image. We will use the ggplot2 package to do this:

It seems like there is a slight increase in average speed for planes that leave with a larger delay. Let’s fit a linear model to quantify the effect:

There is a highly significant effect of 0.034 for the departure delay. This represents the increase in average speed for each minute of delay. So, a plane with 60 minutes of delay will fly 2.04mph faster on average.

Even though the effect is highly significant with a p value of less than 0.0001, its actual effect is negligibly small.

For the second question of interest, we need a slightly more sophisticated model. Since we want to know the effect of the time of day on the arrival delay, we cannot assume a linear effect of the time on the delay. Let’s plot the data:

We plot both the actual delay and our transformed log-delay variable. The smoothing line of the second plot gives a better image of the shape of the delay. It seems that delays are highest at around 8pm, and lowest at 5am. This emphasizes the fact that a linear model would not be appropriate here.

We fit a generalized additive model , a GAM, to this data. Since the response variable is right skewed, a Gamma distribution seems appropriate for the model family. To be able to use it, we have to transform the delay into a strictly positive variable, so we compute the maximum of 1 and the arrival delay for each observation first.

We again see the trend of lower delays in the morning before 6am, and high delays around 8pm. To differentiate between weekdays, we now include this variable in the model:

With this model, we can create an artificial data frame x_new, which we use to plot one prediction line per weekday:

We now see several things:

• The nonlinear trend over the day is the same shape on every day of the week
• Fridays are the worst days to fly by far, with Sunday being a close second. Expected delays are around 20 minutes during rush-hour (8pm)
• Wednesdays and Saturdays are the quietest days
• If you can manage it, fly on a Wednesday morning to minimize expected delays.

Closing remarks

As noted in the beginning of this post, this analysis is only one of many questions that can be tackled with this enormous data set. Feel free to browse the data expo website and especially the „Posters & results“ section for many other interesting analyses.

Der Beitrag A Data Science Case Study in R erschien zuerst auf Statistik Service .

To leave a comment for the author, please follow the link and comment on their blog: R-Programming – Statistik Service . R-bloggers.com offers daily e-mail updates about R news and tutorials about learning R and many other topics. Click here if you're looking to post or find an R/data-science job . Want to share your content on R-bloggers? click here if you have a blog, or here if you don't.

Copyright © 2022 | MH Corporate basic by MH Themes

Never miss an update! Subscribe to R-bloggers to receive e-mails with the latest R posts. (You will not see this message again.)

Case Study: Exploratory Data Analysis in R

Datacamp - david robinson, the united nations voting dataset.

Filtering rows

The vote column in the dataset has a number that represents that country’s vote:

• 2 = Abstain
• 8 = Not present
• 9 = Not a member

One step of data cleaning is removing observations (rows) that you’re not interested in. In this case, you want to remove “Not present” and “Not a member”.

Adding a year column

The next step of data cleaning is manipulating your variables (columns) to make them more informative.

In this case, you have a session column that is hard to interpret intuitively. But since the UN started voting in 1946, and holds one session per year, you can get the year of a UN resolution by adding 1945 to the session number.

Adding a country column

The country codes in the ccode column are what’s called Correlates of War codes. This isn’t ideal for an analysis, since you’d like to work with recognizable country names.

You can use the countrycode package to translate. For example:

Grouping and summarizing

Summarizing the full dataset

In this analysis, you’re going to focus on “% of votes that are yes” as a metric for the “agreeableness” of countries.

You’ll start by finding this summary for the entire dataset: the fraction of all votes in their history that were “yes”. Note that within your call to summarize() , you can use n() to find the total number of votes and mean(vote == 1) to find the fraction of “yes” votes.

Summarizing by year

The summarize() function is especially useful because it can be used within groups .

For example, you might like to know how much the average “agreeableness” of countries changed from year to year. To examine this, you can use group_by() to perform your summary not for the entire dataset, but within each year.

Nice one! The group_by() function must go before your call to summarize() when you’re trying to perform your summary within groups.

Summarizing by country

In the last exercise, you performed a summary of the votes within each year. You could instead summarize() within each country, which would let you compare voting patterns between countries.

Sorting and filtering summarized data

Sorting by percentage of “yes” votes

Now that you’ve summarized the dataset by country, you can start examining it and answering interesting questions.

For example, you might be especially interested in the countries that voted “yes” least often, or the ones that voted “yes” most often.

Filtering summarized output

In the last exercise, you may have noticed that the country that voted least frequently, Zanzibar, had only 2 votes in the entire dataset. You certainly can’t make any substantial conclusions based on that data!

Typically in a progressive analysis, when you find that a few of your observations have very little data while others have plenty, you set some threshold to filter them out.

Visualization with ggplot2

Plotting a line over time

In the last chapter, you learned how to summarize() the votes dataset by year, particularly the percentage of votes in each year that were “yes”.

You’ll now use the ggplot2 package to turn your results into a visualization of the percentage of “yes” votes over time.

Other ggplot2 layers

A line plot is one way to display this data. You could also choose to display it as a scatter plot, with each year represented as a single point. This requires changing the layer (i.e.  geom_line() to geom_point() ).

You can also add additional layers to your graph, such as a smoothing curve with geom_smooth() .

Visualizing by country

Summarizing by year and country

You’re more interested in trends of voting within specific countries than you are in the overall trend. So instead of summarizing just by year, summarize by both year and country, constructing a dataset that shows what fraction of the time each country votes “yes” in each year.

Awesome! Let’s make some plots using this new dataset in the next exercise.

Plotting just the UK over time

Now that you have the percentage of time that each country voted “yes” within each year, you can plot the trend for a particular country. In this case, you’ll look at the trend for just the United Kingdom.

This will involve using filter() on your data before giving it to ggplot2 .

Plotting multiple countries

Plotting just one country at a time is interesting, but you really want to compare trends between countries. For example, suppose you want to compare voting trends for the United States, the UK, France, and India.

You’ll have to filter to include all four of these countries and use another aesthetic (not just x- and y-axes) to distinguish the countries on the resulting visualization. Instead, you’ll use the color aesthetic to represent different countries.

Faceting by country

Faceting the time series

Now you’ll take a look at six countries. While in the previous exercise you used color to represent distinct countries, this gets a little too crowded with six.

Instead, you will facet , giving each country its own sub-plot. To do so, you add a facet_wrap() step after all of your layers.

Faceting with free y-axis

In the previous plot, all six graphs had the same axis limits. This made the changes over time hard to examine for plots with relatively little change.

Instead, you may want to let the plot choose a different y-axis for each facet.

Choose your own countries The purpose of an exploratory data analysis is to ask questions and answer them with data. Now it’s your turn to ask the questions.

You’ll choose some countries whose history you are interested in and add them to the graph. If you want to look up the full list of countries, enter by_country$country in the console.

Linear regression

Linear regression on the United States

A linear regression is a model that lets us examine how one variable changes with respect to another by fitting a best fit line. It is done with the lm() function in R.

Here, you’ll fit a linear regression to just the percentage of “yes” votes from the United States.

Tidying models with broom

Tidying a linear regression model

In the last section, you fit a linear model. Now, you’ll use the tidy() function in the broom package to turn that model into a tidy data frame.

Combining models for multiple countries

One important advantage of changing models to tidied data frames is that they can be combined.

In an earlier section, you fit a linear model to the percentage of “yes” votes for each year in the United States. Now you’ll fit the same model for the United Kingdom and combine the results from both countries.

Awesome! We can easily compare the two models now.

Nesting for multiple models

Nesting a data frame

Right now, the by_year_country data frame has one row per country-vote pair. So that you can model each country individually, you’re going to “nest” all columns besides country , which will result in a data frame with one row per country. The data for each individual country will then be stored in a list column called data .

List columns

This “nested” data has an interesting structure. The second column, data , is a list , a type of R object that hasn’t yet come up in this course that allows complicated objects to be stored within each row. This is because each item of the data column is itself a data frame.

You can use nested$data to access this list column and double brackets to access a particular element. For example, nested$data[[1]] would give you the data frame with Afghanistan’s voting history (the percent_yes per year), since Afghanistan is the first row of the table.

The opposite of the nest() operation is the unnest() operation. This takes each of the data frames in the list column and brings those rows back to the main data frame.

In this exercise, you are just undoing the nest() operation. In the next section, you’ll learn how to fit a model in between these nesting and unnesting steps that makes this process useful.

Fitting multiple models

map() applies an operation to each item in a list

Performing linear regression on each nested dataset

Now that you’ve divided the data for each country into a separate dataset in the data column, you need to fit a linear model to each of these datasets.

The map() function from purrr works by applying a formula to each item in a list, where . represents the individual item. For example, you could add one to each of a list of numbers:

This means that to fit a model to each dataset, you can do:

where . represents each individual item from the data column in by_year_country . Recall that each item in the data column is a dataset that pertains to a specific country.

Tidy each linear regression model

You’ve now performed a linear regression on each nested dataset and have a linear model stored in the list column model . But you can’t recombine the models until you’ve tidied each into a table of coefficients. To do that, you’ll need to use map() one more time and the tidy() function from the broom package.

Recall that you can simply give a function to map() (e.g.  map(models, tidy) ) in order to apply that function to each item of a list.

Unnesting a data frame

You now have a tidied version of each model stored in the tidied column. You want to combine all of those into a large data frame, similar to how you combined the US and UK tidied models earlier. Recall that the unnest() function from tidyr achieves this.

Working with many tidy models

Filtering model terms

You currently have both the intercept and slope terms for each by-country model. You’re probably more interested in how each is changing over time, so you want to focus on the slope terms.

Filtering for significant countries

Not all slopes are significant, and you can use the p-value to guess which are and which are not.

However, when you have lots of p-values, like one for each country, you run into the problem of multiple hypothesis testing, where you have to set a stricter threshold. The p.adjust() function is a simple way to correct for this, where p.adjust(p.value) on a vector of p-values returns a set that you can trust.

Here you’ll add two steps to process the slope_terms dataset: use a mutate to create the new, adjusted p-value column, and filter to filter for those below a .05 threshold.

Great work! Notice that there are now only 61 countries with significant trends.

Sorting by slope

Now that you’ve filtered for countries where the trend is probably not due to chance, you may be interested in countries whose percentage of “yes” votes is changing most quickly over time. Thus, you want to find the countries with the highest and lowest slopes; that is, the estimate column.

Joining datasets

Joining datasets with inner_join

In the first chapter, you created the votes_processed dataset, containing information about each country’s votes. You’ll now combine that with the new descriptions dataset, which includes topic information about each country, so that you can analyze votes within particular topics.

To do this, you’ll make use of the inner_join() function from dplyr .

Filtering the joined dataset

There are six columns in the descriptions dataset (and therefore in the new joined dataset) that describe the topic of a resolution:

• me : Palestinian conflict
• nu : Nuclear weapons and nuclear material
• di : Arms control and disarmament
• hr : Human rights
• co : Colonialism
• ec : Economic development

Each contains a 1 if the resolution is related to this topic and a 0 otherwise.

Visualizing colonialism votes

In an earlier exercise, you graphed the percentage of votes each year where the US voted “yes”. Now you’ll create that same graph, but only for votes related to colonialism.

Using gather to tidy a dataset

In order to represent the joined vote-topic data in a tidy form so we can analyze and graph by topic, we need to transform the data so that each row has one combination of country-vote-topic. This will change the data from having six columns ( me , nu , di , hr , co , ec ) to having two columns ( topic and has_topic ).

Recoding the topics

There’s one more step of data cleaning to make this more interpretable. Right now, topics are represented by two-letter codes:

So that you can interpret the data more easily, recode the data to replace these codes with their full name. You can do that with dplyr ’s recode() function, which replaces values with ones you specify:

Summarize by country, year, and topic

In previous exercises, you summarized the votes dataset by country, by year, and by country-year combination.

Now that you have topic as an additional variable, you can summarize the votes for each combination of country, year, and topic (e.g. for the United States in 2013 on the topic of nuclear weapons.)

Visualizing trends in topics for one country

You can now visualize the trends in percentage “yes” over time for all six topics side-by-side. Here, you’ll visualize them just for the United States.

Tidy modeling by topic and country

Nesting by topic and country

In the last chapter, you constructed a linear model for each country by nesting the data in each country, fitting a model to each dataset, then tidying each model with broom and unnesting the coefficients. The code looked something like this:

Now, you’ll again be modeling change in “percentage” yes over time, but instead of fitting one model for each country, you’ll fit one for each combination of country and topic.

Great work! You can ignore the warning messages in the console for now.

Interpreting tidy models

Now you have both the slope and intercept terms for each model. Just as you did in the last chapter with the tidied coefficients, you’ll need to filter for only the slope terms.

You’ll also have to extract only cases that are statistically significant, which means adjusting the p-value for the number of models, and then filtering to include only significant changes.

Checking models visually

Vanuatu (an island nation in the Pacific Ocean) sharply changed its pattern of voting on the topic of Palestinian conflict.

Let’s examine this country’s voting patterns more closely. Recall that the by_country_year_topic dataset contained one row for each combination of country, year, and topic. You can use that to create a plot of Vanuatu’s voting, faceted by topic.

Phenomenal work! Congratulations on finishing the course!

Gerne beraten wir Sie auch telefonisch & geben Ihnen eine kostenfreie persönliche Auskunft zu Ihrem Projekt.

+49 211 99346512, +41 78 89 11111, +43 720 3035410.

• Konditionen
• Unsere Statistiker
• +49 (0) 211 99346512
• +41 (0) 78 89 11111
• +43 (0) 720 3035410
• +1 (888) 5233685
• Statistik Beratung
• Data Mining Beratung
• Programmierung
• Datenauswertung
• Data Science Beratung

A Data Science Case Study in R

Demanding data science projects are becoming more and more relevant, and the conventional evaluation procedures are often no longer sufficient. For this reason, there is a growing need for tailor-made solutions, which are individually tailored to the project’s goal, which is often implemented by  R programming . T o provide our readers with support in their own R programming, we have carried out an example evaluation which demonstrates several application possibilities of the R programming.

Data Science Projects

Approaching your first data science project can be a daunting task. Luckily, there are rough step-by-step outlines and heuristics than can help you on your way to becoming a data ninja. In this article, we review some of these guidelines and apply them to an example project in R.

For our analysis and the R programming, we will make use of the following R packages:

Anatomy of a Data Science project

A basic data science project consists of the following six steps:

• State the problem you are trying to solve. It has to be an unambiguous question that can be answered with data and a statistical or machine learning model. At least, specify: What is being observed? What has to be predicted?
• Collect the data, then clean and prepare it. This is commonly the most time-consuming task, but it has to be done in order to fit a prediction model with the data.
• Explore the data. Get to know its properties and quirks. Check numerical summaries of your metric variables, tables of the categorical data, and plot univariate and multivariate representations of your variables. By this, you also get an overview of the quality of the data and can find outliers.
• Check if any variables may need to be transformed. Most commonly, this is a logarithmic transformation of skewed measurements such as concentrations or times. Also, some variables might have to be split up into two or more variables.
• Choose a model and train it on the data. If you have more than one candidate model, apply each and evaluate their goodness-of-fit using independent data that was not used for training the model.
• Use the best model to make your final predictions.

We apply the principles on an example data set that was used in the ASA’s 2009 Data expo . The given data are around 120 million commercial and domestic flights within the USA between 1987 and 2008. Measured variables include departure and arrival airport, airline, and scheduled and actual departure and arrival times.

We will focus on the 2008 subset of this data. Because even this is a 600MB subset, it makes sense to start a first analysis on a random sample of this data to be able to quickly explore and develop your code, and then, periodically verify on the real data set that your results are still valid on the complete data.

The following commands read in our subset data and display the first three observations:

Fortunately, the ASA provides a code book with descriptions of each variable here . For example, we now know that for the Variable DayOfWeek, a 1 denotes Monday, a 2 is Tuesday, and so on.

The problem

With this data, it is possible to answer many interesting questions. Examples include:

Do planes with a delayed departure fly with a faster average speed to make up for the delay?

How does the delay of arriving flights vary during the day are planes more delayed on weekends.

• How has the market share of different airlines shifted over these 20 years?
• Are there specific planes that tend to have longer delays? What characterizes them? Maybe the age, or the manufacturer?

Additionally to these concrete questions, the possibilities for explorative, sandbox-style data analysis are nearly limitless.

Here, we will focus on the first two boldened questions.

Data cleaning

You should always check out the amount of missing values in your data. For this, we write an sapply-loop over each column in the flights data and report the percentage of missing values:

We see that most variables have at most a negligible amount of missing values. However, the last five variables, starting at the CarrierDelay, show almost 80% missing values. This is usually an alarmingly high amount of missing data that would suggest dropping this variable from the analysis altogether, since not even a sophisticated imputing procedure can help here. But, as further inspection shows, these variables only apply for delayed flights, i.e. a positive value in the ArrDelay column.

When selecting only the arrival delay and the five sub-categories of delays, we see that they add up to the total arrival delay. For our analysis here, we are not interested in the delay reason, but view only the total ArrDelay as our outcome of interest.

The pipe operator %>%, by the way, is a nice feature of the magrittr package (also implemented in dplyr) that resembles the UNIX-style pipe. The following two lines mean and do exactly the same thing, but the second version is much easier to read:

The pipe operator thus takes the output of the left expression, and makes it the first argument of the right expression.

We have surprisingly clean data where not much has to be done before proceeding to feature engineering.

Explorative analyses

Our main variables of interest are:

• The date, which conveniently is already split up in the columns Year, Month, and DayOfMonth, and even contains the weekday in DayOfWeek. This is rarely the case, you mostly get a single column with a name like date and entries such as “2016-06-24”. In that case, the R package lubridate provides helpful functions to efficiently work with and manipulate these dates.
• CRSDepTime, the scheduled departure time. This will indicate the time of day for our analysis of when flights tend to have higher delays.
• ArrDelay, the delay in minutes at arrival. We use this variable (rather than the delay at departure) for the outcome in our first analysis, since the arrival delay is what has the impact on our day.
• For our second question of whether planes with delayed departure fly faster, we need DepDelay, the delay in minutes at departure, as well as a measure of average speed while flying. This variable is not available, but we can compute it from the available variables Distance and AirTime. We will do that in the next section, “Feature Engineering”.

Let’s have an exploratory look at all our variables of interest.

Brauchen Sie Hilfe?

Gerne können Sie bei uns auch eine unverbindliche Beratung sowie einen kostenlosen Kostenvoranschlag erhalten. Wir beraten Sie gerne!

• info@novustat.com

Jetzt unverbindlich anfragen

Flight date

Since these are exploratory analyses that you usually won’t show anyone else, spending time on pretty graphics does not make sense here. For quick overviews, I mostly use the standard graphics functions from R, without much decoration in terms of titles, colors, and such.

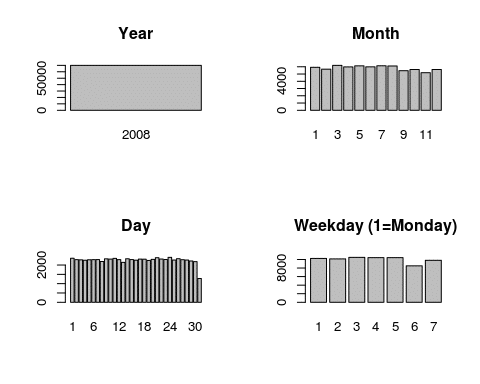
Since we subsetted the data beforehand, it makes sense that all our flights are from 2008. We also see no big changes between the months. There is a slight drop after August, but the remaining changes can be explained by the number of days in a month.

The day of the month shows no influence on the amount of flights, as expected. The fact that the 31st has around half the flights of all other days is also obvious.

When plotting flights per weekday, however, we see that Saturday is the most quiet day of the week, with Sunday being the second most relaxed day. Between the remaining weekdays, there is little variation.

Departure Time

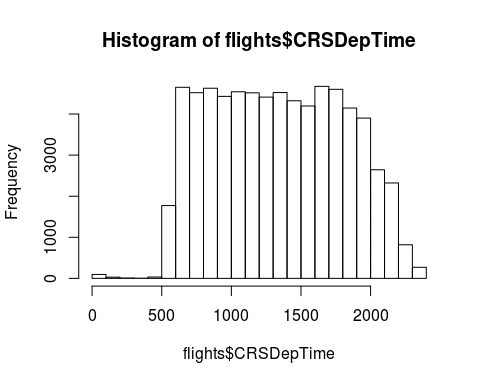
A histogram of the departure time shows that the number of flights is relatively constant from 6am to around 8pm and dropping off heavily before and after that.

Arrival and departure delay

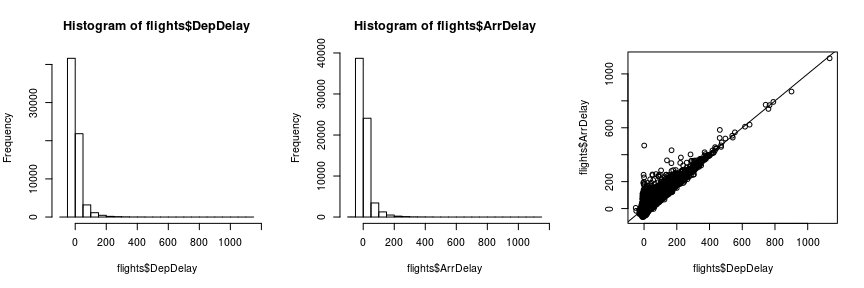
Both arrival and departure delay show a very asymmetric, right-skewed distribution. We should keep this in mind and think about a logarithmic transformation or some other method of acknowledging this fact later.

The structure of the third plot of departure vs. arrival delay suggests that flights that start with a delay usually don’t compensate that delay during the flight. The arrival delay is almost always at least as large as the departure delay.

To get a first overview for our question of how the departure time influences the average delay, we can also plot the departure time against the arrival delay:

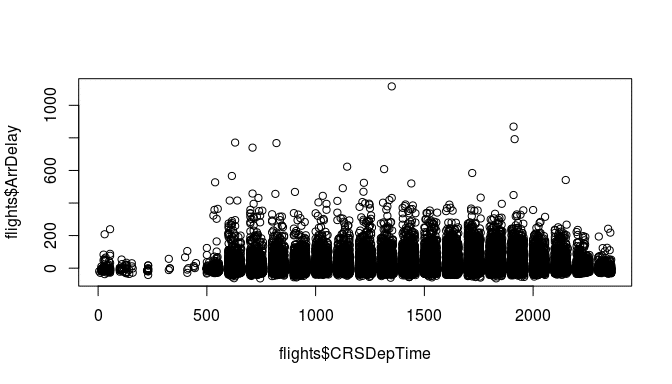
Aha! Something looks weird here. There seem to be periods of times with no flights at all. To see what is going on here, look at how the departure time is coded in the data:

A departure of 2:55pm is written as an integer 1455. This explains why the values from 1460 to 1499 are impossible. In the feature engineering step, we will have to recode this variable in a meaningful way to be able to model it correctly.

Distance and AirTime

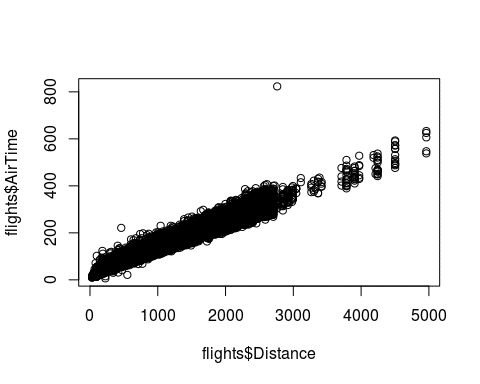
Plotting the distance against the time needed, we see a linear relationship as expected, with one large outlier. This one point denotes a flight of 2762 miles and an air time of 823 minutes, suggesting an average speed of 201mph. I doubt planes can fly at this speed, so we should maybe remove this observation.

Feature Engineering

Feature engineering describes the manipulation of your data set to create variables that a learning algorithm can work with. Often, this consists of transforming a variable (through e.g. a logarithm), or extracting specific information from a variable (e.g. the year from a date string), or converting something like the ZIP code to a

For our data, we have the following tasks:

• Convert the weekday into a factor variable so it doesn’t get interpreted linearly.
• Create a log-transformed version of the arrival and departure delay.
• Transform the departure time so that it can be used in a model.
• Create the average speed from the distance and air time variables.

Converting the weekday into a factor is important because otherwise, it would be interpreted as a metric variable, which would result in a linear effect. We want the weekdays to be categories, however, and so we create a factor with nice labels:

log-transform delay times

When looking at the delays, we note that there are a lot of negative values in the data. These denote flights that left or arrived earlier than scheduled. To allow a log-transformation, we set all negative values to zero, which we interpret as “on time”:

Now, since there are zeros in these variables, we create the variables log(1+ArrDelay) and log(1+DepDelay):

Transform the departure time

The departure time is coded in the format hhmm, which is not helpful for modelling, since we need equal distances between equal durations of time. This way, the distance between 10:10pm and 10:20pm would be 10, but the distance between 10:50pm and 11:00pm, the same 10 minutes, would be 50.

For the departure time, we therefore need to convert the time format. We will use a decimal format, so that 11:00am becomes 11, 11:15am becomes 11.25, and 11:45 becomes 11.75.

The mathematical rule to transform the “old” time in hhmm-format into a decimal format is:

Here, the first part of the sum generates the hours, and the second part takes the remainder when dividing by 100 (i.e., the last two digits), and divides them by 60 to transform the minutes into a fraction of one hour.

Let’s implement that in R:

Of course, you should always verify that your code did what you intended by checking the results.

Create average speed

The average flight speed is not available in the data – we have to compute it from the distance and the air time:

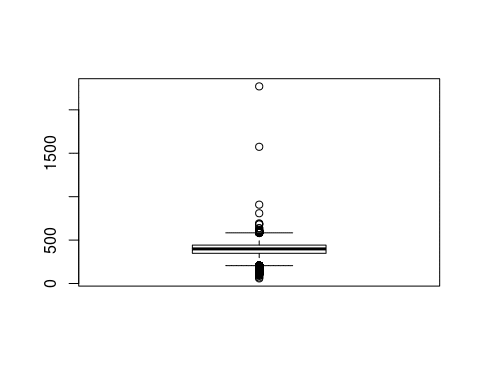
We have a few outliers with very high, implausible average speeds. Domain knowledge or a quick Google search can tell us that speeds of more than 800mph are not maintainable with current passenger planes. Thus, we will remove these flights from the data:

Choosing an appropriate Method

For building an actual model with your data, you have the choice between two worlds, statistical modelling and machine learning.

Broadly speaking, statistical models focus more on quantifying and interpreting the relationships between input variables and the outcome. This is the case in situations such as clinical studies, where the main goal is to describe the effect of a new medication.

Machine learning methods on the other hand focus on achieving a high accuracy in prediction, sometimes sacrificing interpretability. This results in what is called “black box” algorithms, which are good at predicting the outcome, but it’s hard to see how a model computes a prediction for the outcome. A classic example for a question where machine learning is the appropriate answer is the product recommendation algorithm on online shopping websites.

For our questions, we are interested in the effects of certain input variables (speed and time of day / week). Thus we will make use of statistical models, namely a linear model and a generalized additive model.

To answer our first question, we first plot the variables of interest to get a first impression of the relationship. Since these plots will likely make it to the final report or at least a presentation to your supervisors, it now makes sense to spend a little time on generating a pretty image. We will use the ggplot2 package to do this:

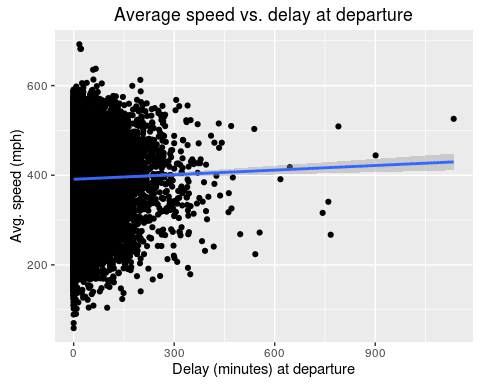
It seems like there is a slight increase in average speed for planes that leave with a larger delay. Let’s fit a linear model to quantify the effect:

There is a highly significant effect of 0.034 for the departure delay. This represents the increase in average speed for each minute of delay. So, a plane with 60 minutes of delay will fly 2.04mph faster on average.

Even though the effect is highly significant with a p value of less than 0.0001, its actual effect is negligibly small.

For the second question of interest, we need a slightly more sophisticated model. Since we want to know the effect of the time of day on the arrival delay, we cannot assume a linear effect of the time on the delay. Let’s plot the data:

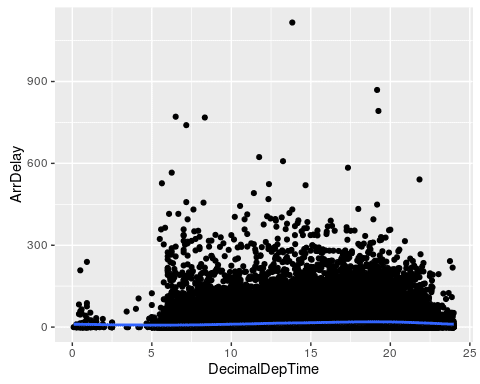
We plot both the actual delay and our transformed log-delay variable. The smoothing line of the second plot gives a better image of the shape of the delay. It seems that delays are highest at around 8pm, and lowest at 5am. This emphasizes the fact that a linear model would not be appropriate here.

We fit a generalized additive model , a GAM, to this data. Since the response variable is right skewed, a Gamma distribution seems appropriate for the model family. To be able to use it, we have to transform the delay into a strictly positive variable, so we compute the maximum of 1 and the arrival delay for each observation first.

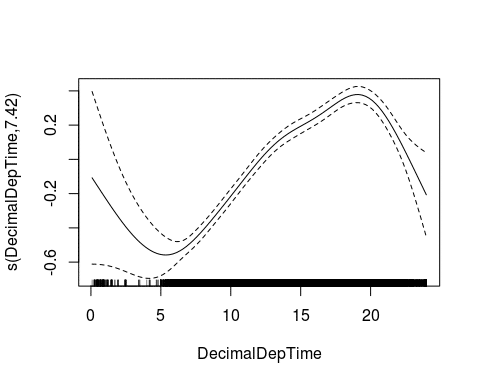
We again see the trend of lower delays in the morning before 6am, and high delays around 8pm. To differentiate between weekdays, we now include this variable in the model:

With this model, we can create an artificial data frame x_new, which we use to plot one prediction line per weekday:

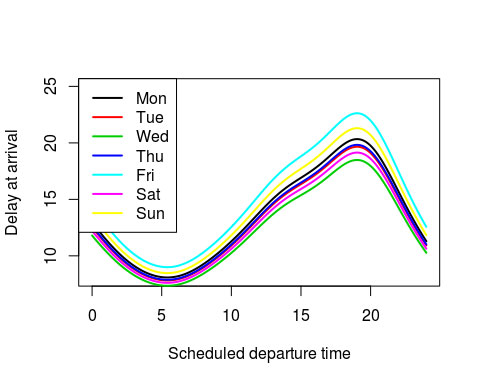
We now see several things:

• The nonlinear trend over the day is the same shape on every day of the week
• Fridays are the worst days to fly by far, with Sunday being a close second. Expected delays are around 20 minutes during rush-hour (8pm)
• Wednesdays and Saturdays are the quietest days
• If you can manage it, fly on a Wednesday morning to minimize expected delays.

Closing remarks

As noted in the beginning of this post, this analysis is only one of many questions that can be tackled with this enormous data set. Feel free to browse the data expo website and especially the “Posters & results” section for many other interesting analyses.

Wir benötigen Ihre Zustimmung, bevor Sie unsere Website weiter besuchen können. Wir verwenden Cookies und andere Technologien auf unserer Website. Einige von ihnen sind essenziell, während andere uns helfen, diese Website und Ihre Erfahrung zu verbessern. Personenbezogene Daten können verarbeitet werden (z. B. IP-Adressen), z. B. für personalisierte Anzeigen und Inhalte oder Anzeigen- und Inhaltsmessung. Weitere Informationen über die Verwendung Ihrer Daten finden Sie in unserer Datenschutzerklärung . Sie können Ihre Auswahl jederzeit unter Einstellungen widerrufen oder anpassen.

• Statistiken
• Externe Medien

Alle akzeptieren

Nur essenzielle Cookies akzeptieren

Individuelle Datenschutzeinstellungen

Cookie-Details Datenschutzerklärung Impressum

Wir verwenden Cookies und andere Technologien auf unserer Website. Einige von ihnen sind essenziell, während andere uns helfen, diese Website und Ihre Erfahrung zu verbessern. Personenbezogene Daten können verarbeitet werden (z. B. IP-Adressen), z. B. für personalisierte Anzeigen und Inhalte oder Anzeigen- und Inhaltsmessung. Weitere Informationen über die Verwendung Ihrer Daten finden Sie in unserer Datenschutzerklärung . Hier finden Sie eine Übersicht über alle verwendeten Cookies. Sie können Ihre Einwilligung zu ganzen Kategorien geben oder sich weitere Informationen anzeigen lassen und so nur bestimmte Cookies auswählen.

Alle akzeptieren Speichern Nur essenzielle Cookies akzeptieren

Essenzielle Cookies ermöglichen grundlegende Funktionen und sind für die einwandfreie Funktion der Website erforderlich.

Cookie-Informationen anzeigen Cookie-Informationen ausblenden

Statistik Cookies erfassen Informationen anonym. Diese Informationen helfen uns zu verstehen, wie unsere Besucher unsere Website nutzen.

Marketing-Cookies werden von Drittanbietern oder Publishern verwendet, um personalisierte Werbung anzuzeigen. Sie tun dies, indem sie Besucher über Websites hinweg verfolgen.

Inhalte von Videoplattformen und Social-Media-Plattformen werden standardmäßig blockiert. Wenn Cookies von externen Medien akzeptiert werden, bedarf der Zugriff auf diese Inhalte keiner manuellen Einwilligung mehr.

Datenschutzerklärung Impressum

Navigation Menu

Search code, repositories, users, issues, pull requests..., provide feedback.

We read every piece of feedback, and take your input very seriously.

Saved searches

Use saved searches to filter your results more quickly.

To see all available qualifiers, see our documentation .

• Notifications You must be signed in to change notification settings

data manipulation and visualization like dplyr and ggplot2

allanbeto/Exploratory_Data_Analysis_in_R_Case_Study

Folders and files.